LC・RLC共振回路の共振周波数の求め方

共振回路とは，ある特定の周波数の信号に対して電流が大きく振動するような回路のことです。 このような特性は，交流の概論で紹介されていた回路の構成に利用されます。

共振回路では，以下のようにコイルとコンデンサーを直列に繋いだ回路が基本となります。

では，これからこの回路の特性を調べていきましょう。

回路を流れる電流を $I(t)$ と書くことにします。 するとキルヒホッフ則から，以下のような回路方程式が成り立ちます。 $$\begin{aligned} L\frac{dI(t)}{dt} + \frac{Q(t)}{C} = 0 \end{aligned}$$ ここで $Q$ はコンデンサーに蓄えられた電荷なので $$\begin{aligned} \frac{dQ(t)}{dt} = I(t) \end{aligned}$$ が成り立ちます。 結局 $Q(t)$ は $I(t)$ で書けるので回路方程式の両辺を微分して方程式を整理しましょう。 もとの回路方程式は以下のようにも書けます。 $$\begin{aligned} \frac{d^2I(t)}{d t^2} = - \left(\frac{1}{\sqrt{LC}}\right)^2 I(t) \end{aligned}$$ さて，この微分方程式に見覚えはありませんか？ これはバネの単振動を表す式と全く同じ形をしています！ 単振動まとめで学んだことを用いれば，電流 $I(t)$ が以下の周波数で振動することが分かります。

RLC回路への準備も兼ねて，コイルとコンデンサーだけでなく抵抗も繋いで拡張した回路を考えてみましょう。 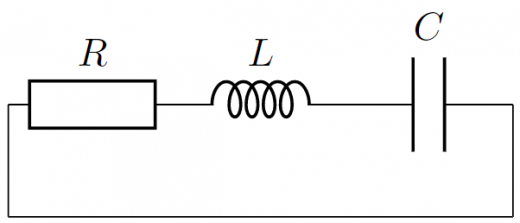すると，キルヒホッフ則から以下のような回路方程式が成り立ちます。 $$\begin{aligned} RI(t)+L\frac{dI(t)}{dt} + \frac{Q(t)}{C} = 0 \end{aligned}$$ 先ほどと同様に式を整理すると，以下のように書き換えられます。 $$\begin{aligned} \frac{d^2I(t)}{d t^2} +\frac{R}{L}\frac{dI(t)}{dt} +\frac{1}{LC}I(t) = 0 \end{aligned}$$

仮に $I(t)$ をバネの付けられたおもりの位置と見なすと，第二項はおもりの速度に比例する摩擦項と理解できます。 この方程式は斉次二階線形微分方程式と呼ばれるもので， $$\begin{aligned} \{e^{i\omega t}\} \end{aligned}$$ という形の関数の足し合わせで全ての解を尽くせるということが知られています。 $I(t)$ が $e^{i\omega t}$ という形の関数だとして，微分方程式に代入すると $$\begin{aligned} (i\omega)^2 + \frac{R}{L}(i\omega)+\frac{1}{LC} = 0 \end{aligned}$$ が成り立つことが分かります。 この二次方程式を解けば $$\begin{aligned} i\omega = -\frac{R}{2L} \pm i\sqrt{\frac{1}{LC}-\left(\frac{R}{2L}\right)^2} \end{aligned}$$ だと分かります。 つまり，$I(t)$ は $A,B$ を定数として $$\begin{aligned} I(t) =　Ae^{-\frac{R}{2L}t+i\sqrt{1/LC-(R/2L)^2}\:t} +Be^{-\frac{R}{2L}t-i\sqrt{1/LC-(R/2L)^2}\:t} \end{aligned}$$ と書けます。 時刻 $t=0$ での電流の値を $I_0$ とし，$I(t)$ が常に実数であることに注意すると $$\begin{aligned} A = B = \frac{I_0}{2} \end{aligned}$$ でなければならないので，結局電流 $I(t)$ は $$\begin{aligned} I(t) = I_0 e^{-\frac{R}{2L}t}\cos\left( \sqrt{1/LC-(R/2L)^2}\:t \right) \end{aligned}$$ だと求まります。 電流 $I(t)$ は振動しながらも減衰していくことが分かりますね。 これは電流が抵抗器を流れる際にジュール熱としてエネルギーが消費されてしまうためです。 また，$R\rightarrow 0$ とすると抵抗が無い場合と一致することも確認できます。