ホイートストンブリッジ回路の公式の証明と応用

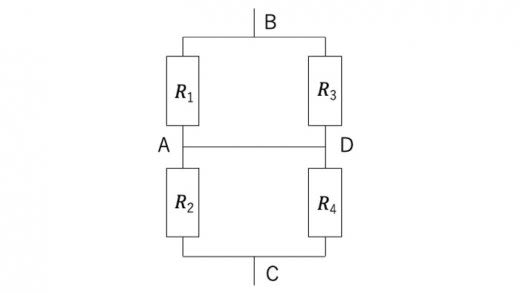
ホイートストンブリッジとは，下図のように回路内に架橋部分が存在するブリッジ回路のことを言います。

ホイートストンブリッジでは，以下のような事実が成り立ちます。

(1)式はホイートストンブリッジの平衡条件とも呼ばれます。

この証明に電圧 $V$ が出てきていないことに注意してください。これより，ホイートストンブリッジの公式は，用いている電圧の値とは関係なしに用いることができます。これがこの公式の強力な点です。

ここでは，テブナンの定理を用いてホイートストンブリッジの性質について考えてみます。

テブナンの定理

テブナンの定理について，軽く説明します。

テブナンの定理とは，複雑な回路のある箇所に流れる電流を求める際に，等価で簡単な回路に組み替えることができるという定理です。具体的には，以下のような手順を踏みます。

テブナンの定理による解析

テブナンの定理を用いるために，図1の回路を下図のように区間BCとそれ以外とに分割し，それぞれ領域1，2と呼びます。

まず，領域2の等価電源を求めます。直列回路内の電圧降下は抵抗値に比例することから考えて，点Xでの電位を $V_X$ とすると，点B，Cでの電位はそれぞれ

$$V_B = \dfrac{R_3}{R_1 + R_3} V , V_C = \dfrac{R_4}{R_2 + R_{4}} V$$

となるから，区間BCの電位差 $V_{BC}$ は，

$$V_{BC} = \left(\dfrac{R_3}{R_1 + R_3} - \dfrac{R_4}{R_2 + R_{4}} \right) V$$

となります。

次いで，領域2の等価抵抗を求めます。テブナンの定理を用いる際，抵抗の図は下図のように書き換えられます。

直列および並行接続された抵抗の合成抵抗の求め方を利用して，等価抵抗 $R$ は

$$R =\dfrac{R_1 R_2}{R_1 + R_2} + \dfrac{R_3 R_4}{R_3 + R_4}$$

となります。

したがって，テブナンの定理を用いると，図1は下図のような等価な回路に書き換えることができます。

したがって，区間BCに流れる電流を電流を $I$ とおくと，，

$$I = \dfrac{V_{BC}}{R + R_5} = \dfrac{1}{R + R_5} \left(\dfrac{R_3}{R_1 + R_3} - \dfrac{R_4}{R_2 + R_{4}} \right) V$$

となるので，$I =0$ となる条件は

$$\dfrac{R_3}{R_1 + R_3} - \dfrac{R_4}{R_2 + R_{4}} =0$$

この式を変形すると(1)式を得ることができます。

ここでは，ホイートストンブリッジについて実用的な観点から述べます。高校物理ではこれから説明するような状況での問題も出ることがあるので，一度知っておくと良いと思います。

未知の抵抗値の測定

先ほど示した事実を用いると，ホイートストンブリッジに使用する抵抗は，3つ抵抗値が既知のものを使用すれば，抵抗値が未知の抵抗の抵抗値を知ることができます。

このように区間BDに検流計，区間BCに可変抵抗器(抵抗値を変えることのできる抵抗です)を用いることで，検流計が0となったときの抵抗値 $R_3$ を使って，未知の抵抗値 $R_4$ を求めることができます。

検流計の内部抵抗によらず未知の抵抗値を求めることができていることがポイントです。

メートルブリッジへの応用

ホイートストンブリッジの仕組みをうまく応用することで，未知の抵抗値の測定に必要な既知抵抗の数を減らすことができます。それがメートルブリッジです。

上図のように，区間ACに材質が一様で太さが一定であり，長さが $L$ の抵抗線を接続します。 オームの法則と抵抗の性質 で説明したように，抵抗率 $\rho$，長さ $l$，底面積 $S$ の抵抗線の抵抗 $R$ は，

$$R = \rho \dfrac{l}{S}$$

で与えられます。

いま抵抗線の材質は一様で，太さも一定なので，抵抗線の抵抗はその長さに比例することになります。

いま，検流計が0を示したとき，区間ABの長さが長さが $x$ であったとすると，先ほど考えたことより

$$R_1 : R_3 = x : L -x$$

$$\therefore \dfrac{R_1}{R_3} = \dfrac{x}{L-x}$$

これより，未知抵抗の抵抗値 $R_4$ は，

$$R_4 = \dfrac{R_2}{R_1} R_3 = \dfrac{L-x}{x} R_3$$

と求めることができます。