コンデンサーを含む回路の解法
回路の問題でコンデンサーを扱う際に,いくつか注意しなければならない点について解説します。
回路でのコンデンサーの役割
回路でのコンデンサーの役割
詳しい説明は コンデンサーの理論 に譲りますが,回路においてコンデンサーは電荷の充電・放電を担います。コンデンサーは一言で言えば,電荷のプールなのです。
以下では,簡単のため,初めコンデンサーは電荷を蓄えていないものとします。
この記事に関連するQ&A
回路において考察すべきコンデンサーの物理量
回路において考察すべきコンデンサーの物理量
回路の問題を解く上で考えるべき,コンデンサーに関する物理量について説明します。
コンデンサーが蓄える電荷
コンデンサーについて,以下の事実が成り立ちます。
コンデンサーが初め電荷を蓄えていないとき,コンデンサーが蓄える電荷は,極板の外側は0であり,極板の内側どうしは同じ絶対値で符号は逆である。
これを静電誘導を用いて証明してみましょう。
以下のように,コンデンサーの両極板に電荷が蓄えられているとする。コンデンサーを構成するのは導体であるから,静電誘導により,コンデンサーの外側にのみ電荷が分布することに注意する。

さらに静電誘導により,コンデンサー内の電場は0にならなければならない。ここで,以下のような面積 の金属平板に電荷 が蓄えられているとき,その平板から放たれる電場 は
であることに注意する。図の上向きを正とすると,上側の極板内部について
下側の極板内部について
(1)-(2) より
(1) + (2) より
また,コンデンサーの外側では電場は とみなしてよいから
(3)と合わせて
(4)と(6)より
また,複数のコンデンサーが接続されている場合,電荷保存則を考えることが必要になる場面があります。
複数のコンデンサーが接続されているとき,接続されている極板間で蓄えられている電荷の総量は保存される。
具体的な用い方は,この後の例題で確認してみます。
コンデンサーで発生する電圧
電荷を蓄えているコンデンサーには電圧が生じています。キルヒホッフの法則から回路方程式を考える際にはこれを定式化しなければなりません。
電気容量 のコンデンサーが電荷 を蓄えているとき,コンデンサーで生じる電圧 は
と表される。
証明について,詳しくは コンデンサーの理論 をご覧ください。
コンデンサーが蓄えるエネルギー
回路の問題を扱う際には,エネルギーの視点から考えることも必要になります。コンデンサーは電荷を蓄えているときに静電エネルギーも蓄えているため,このエネルギーを考えることを忘れないようにしましょう。
コンデンサーの蓄える静電エネルギーは以下の表式で与えられます。
電気容量 のコンデンサーが 電荷 を蓄えており,電圧 が加わっているとき,コンデンサーが蓄えている静電エネルギー は
と表される。
証明について,詳しくは コンデンサーの理論 をご覧ください。
初期状態・定常状態のコンデンサー
初期状態・定常状態のコンデンサー
初期状態と定常状態でのコンデンサーの振る舞いを考える上で注目すべき点について説明します。
初期状態について
回路中のコンデンサーの初期状態について,以下の事実が成り立ちます。
回路内のコンデンサーは,その初期状態において,回路に接続される前と電荷は変わらない。
電荷が,瞬時に移動することは有り得ませんから,コンデンサーに蓄えられている電荷の量も当然連続 (ここでは関数の連続性と微分可能性の意味と関係 で使われる連続の意味です) で変化することになります。
定常状態について
コンデンサーの定常状態について,以下の事実が成り立ちます。
定常状態のコンデンサーには電流が流れない。
これが成り立つことは,以下のように考えれば説明できます。
コンデンサーにおける定常状態とは,「蓄えられている電荷の量が変化しない」ことを表します。もし定常状態のコンデンサーに電流が流れているとすると,コンデンサーの極板上の電荷量も変化することになるので,コンデンサーが定常状態であることに反してしまいます。
コンデンサーを含む回路の問題の解き方
コンデンサーを含む回路の問題の解き方
例題を考えることで,回路におけるコンデンサーの扱い方を確認しておきましょう。
まずは,コンデンサーとコイルを組み合わせた回路について考えてみましょう。
以下のような直流電源を含む回路を考える。ただし回路内のSはスイッチを指す。また,初めにコンデンサーには電荷は蓄えられていないものとする。
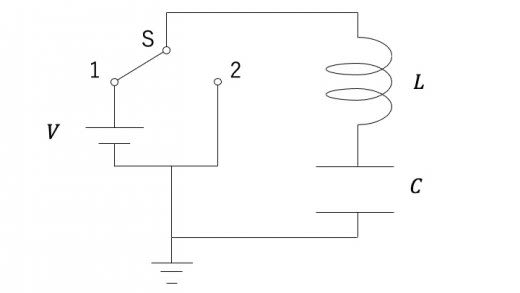
まずスイッチを1に入れる。
(1)回路を流れる電流を,横軸を時刻にとったグラフで表したとき,原点での傾きを求めよ。スイッチを1に入れた瞬間に計測を始めたとする。
(2)定常状態になったとき,コンデンサーに蓄えられている電荷と回路に流れている電流をそれぞれ求めよ。
定常状態になったのち,スイッチを1から2につなぎかえる。
(3)スイッチをつなぎかえてから 秒後にコンデンサーに蓄えられている電荷と回路に流れている電流をそれぞれ求めよ。
(4)この状態ではエネルギーが保存されていることを示せ。
解答に移る前に,コイルの性質について簡単に説明します。自己インダクタンス のコイルに電流 が流れているとき,コイルで生じる電圧降下 は
であり,このときコイルが蓄えているエネルギー は (磁場エネルギーと呼ばれます)
詳しくは別の記事での解説をご参照ください。
それでは解答例に移ります。
(1)はじめ,コンデンサーに蓄えられている電荷は なので,スイッチを1に入れた直後もコンデンサーに蓄えられている電荷は 。キルヒホッフの第二法則より
求める値とは に他ならないので,求めるべき値は である。
(2)定常状態になったとき,コンデンサーに流れる電流は になる。この問題の回路には分岐がないから,求める電流 の値は
さらに,この電流は定常状態では一定値となるから,コイルでの電圧降下は生じない。求める電荷の値を とおくと,キルヒホッフの第二法則より
(3)(2)までの と今後用いる は別の文字として扱う。
スイッチを1から2につなぎかえると,コンデンサーは放電を始める。 秒後にコンデンサーに蓄えられている電荷を ,回路を流れる電流を とおく。
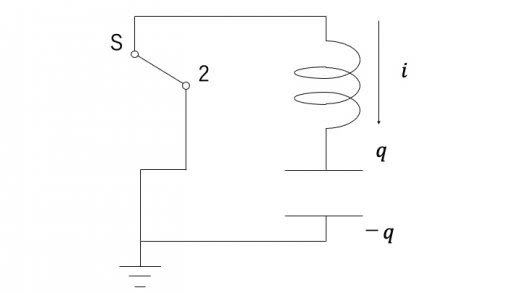
キルヒホッフの第二法則より
図3での定め方より
以降,簡単のため微分に関してニュートンの記法を用いる。
(2)を(1)に用いて変形して
これは,力学での単振動の式と数学的に同じ形をしているため,解も同じ形で与えられる (詳しくは単振動のまとめをご覧ください)。
したがって
ただし
スイッチをつなぎかえた直後,即ち では,コンデンサーの初期状態について解説したときと同様の理由で , であるから,上式に代入し整理して
よって,求める電荷 ,電流 は,それぞれ
(4)回路内に蓄えられているエネルギーを とおく。時刻 においてコンデンサーが蓄えている静電エネルギー は
時刻 においてコイルが蓄えている磁場エネルギー は
したがって
一方, については, では,, であることより
したがって,
であることがわかるから,この系のエネルギーは保存される。
次に,コンデンサーと抵抗を含む回路について考えてみましょう。
以下のような回路を考える。

初め各コンデンサーに蓄えられている電荷は0とする。次の問いに答えよ。
(1)初め回路に流れている電流を求めよ。
(2)定常状態になったとき,各コンデンサーに蓄えられている電荷をそれぞれ求めよ。
(3)回路が定常状態になるまで抵抗で消費されたジュール熱を求めよ。
(1)初め,各コンデンサーに蓄えられている電荷はそれぞれ のままだから,求める電流を とおくと,キルヒホッフの第二法則より
(2)定常状態になったとき,コンデンサー1,2,3に蓄えられている電荷をそれぞれ ,, とおく。このとき回路に流れている電流は になるから,キルヒホッフの第二法則より
また,下図の赤丸部分では電荷保存則が成り立つから,
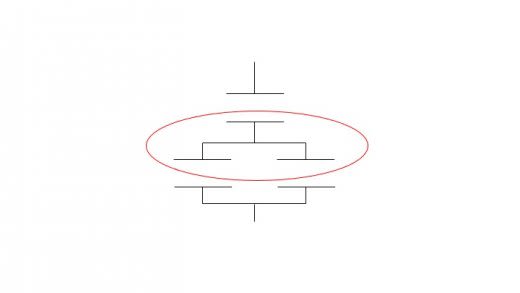
まず(2)より
(2’),(3)より
(1)に代入して
ここから
(3)抵抗と各コンデンサー及び導線を系とみなす。系に送られた電荷の総量は であるから,電荷が系になした仕事 は,それぞれ
コンデンサー1,2,3が蓄えている静電エネルギーの合計 は,
よって,求めるジュール熱を とすると,熱力学第一法則 (詳しくは 熱力学第一法則|仕事と内部エネルギーの関係 をご覧ください) またはエネルギー保存則より
初期状態と定常状態でのコンデンサーの挙動は特に注意が必要です。











