レンズの公式｜凸レンズ,凹レンズ,焦点距離等の用語の定義

レンズ面以外の1点からの光がレンズ面に入射したとき，全ての光が再び1点に集められるように設計された道具のことをレンズと定義します。

一般にレンズは丸みを帯びた形状をしていますが，ここではレンズは十分薄く，板のような形（平面に投射すると1本の線分）に表せるという理想化を行っています。

主なレンズの種類として凸レンズと凹レンズがあります。それぞれレンズが凸面，凹面になっており，光源から出た光はそれぞれ上図，下図のように屈折します。

上図（凸レンズ）について，$\mathrm{BC}$ を通る線分は凸レンズ，点 $\mathrm{A}$ は光源，点 $\mathrm{E}$ は像に対応しています。

凸レンズでは，無限遠の光源からの平行光線がレンズに屈折されて集まる点を焦点と言い，レンズと焦点の距離を焦点距離と言います。レンズの定義から，そのような点は平行光線が右側から入射した場合と，左側から入射した場合に対応する２つのみが存在します。

例えば上図の凸レンズの場合，直線 $\mathrm{AB}$ と直線 $\mathrm{CD}$ がレンズに平行に入射しています。よって，焦点の1つはこれら2つの直線が屈折した直線の交点，点 $\mathrm{D}$ とわかります。

下図（凹レンズ）について，図は平行光線が凹レンズに入射した時の光の経路を表しています。凹レンズでは，凸レンズのように平行光線が交わる点が存在しません。ただ，平行光線が屈折してできる線を延長したとき，凸レンズとは逆側に交わる点が生じます。この点を凹レンズでは焦点といいます。下図では焦点は $\mathrm{A'}$ となります。ここで右方から光が逆に来たと考えると，レンズがなければ光は $\mathrm{A'}$ の位置に像を結ぶと考えられます。このような仮想的実像の位置を虚物体(虚光源)と言います。

また，上図の点線の長さ，つまりレンズの中点を通り，レンズと直交する直線から，光源と像への距離をそれぞれ，光源，像の大きさといいます。また，光源の大きさと像の大きさの比をレンズの倍率と言います。

光源の位置とレンズの位置，焦点の位置が与えられた時に像を作図する手順は以下の通りです。

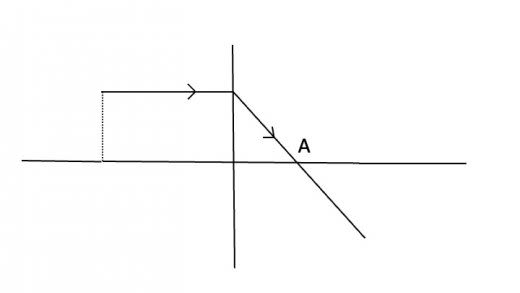
まず，光源からレンズに平行な直線を引き，焦点を通るように屈折させた直線を書きます。

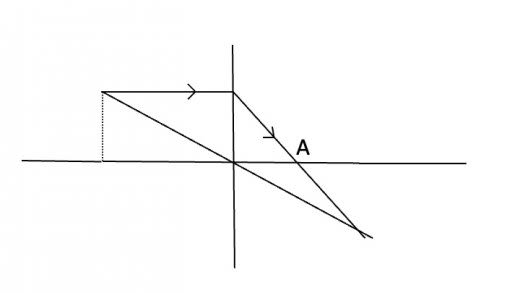
次にレンズの中点を通るような直線を引きます。このような直線はいつも直進するので，描いた直線が交わる点の位置が，像のできる位置となります。

以上で示した手順で作図すると，焦点とレンズの間に光源があった時，上図のように，直線が交点を持たなくなってしまうことがわかると思います。 このような時，上図のように半直線を延長したものが交わる点 $\mathrm{X}$ は，レンズの右側から見ると，光はあたかも点 $\mathrm{X}$ から来たように見えます。このような点を実像とは異なる概念として，虚像と言います。

凹レンズの場合や，虚像ができる場合も同様に，2つの相似の三角形を見つけ，辺に関する関係式を整理することでレンズの公式を導くことができます。

• 平行光線では，屈折する前は全ての光の位相が揃っています。しかし焦点の位置以外では，屈折により生じる位相差により，異なる位相で干渉し，像は生じません。

• 光の逆行性及びフェルマーの原理を考えると，全ての経路における光の所要時間は同一です。つまり短い経路上には光学距離を長くするような媒質(つまりここではレンズ)が余分にあると考えられます。故に焦点に光が集まる場合，レンズは凸型になります。