1、三角形$ABC$において,$AB=2$,$BC=1+ \sqrt{5}$,$CA=2\sqrt{2}$とする.

こんにちは、$\text{Enigmathematics}$です

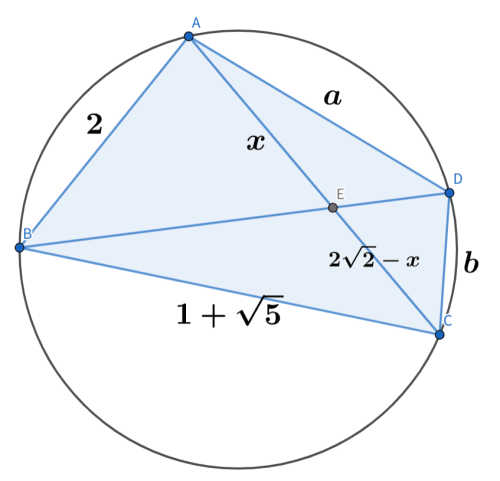
早速ですが、線分$AE$の長さをどうやって求めていくのか見ていきたいと思います...(ご参考までに、一番下にGeoGebraで作成した簡易的な図を置いています)

問題文にある通り、外接円ときたら色々性質が浮かびますが、今回は「対角の和

が$180°$になる」という性質を用いてうまく条件を捌いていきましょう

初めに、$AE=x$とおき、

$∠BAD=\pi-∠DCB$より、

$$\begin{align*}S_1&=\dfrac{1}{2}・2a\sin ∠BAD\\S_2&=\dfrac{1}{2}・(1+\sqrt{5})b \sin (\pi-∠DCB)=\dfrac{1}{2}・(1+\sqrt{5})b\sin ∠BAD\\&\text{さらに、}　 \dfrac{S_1}{S_2}=\sqrt{5}-1\text{より、}\\\sqrt{5}-1&=\dfrac{2a}{(1+\sqrt{5})b}\end{align*}$$

$$∴a=2b$$

ここまできて、$a,b$の値を具体的に出したくなりますが、敢えて放っておきましょう

次に、内接する四角形の中にある三角形の相似の性質を用います

$△AEB∽△DEC$が従うので

$$2:x:BE=b:DE:2\sqrt{2}-x$$

よって、$BE=\dfrac{2(2\sqrt{2}-x)}{b},\ \ DE=\dfrac{bx}{2}$

さらに、$△AED∽△BEC$も従うので、ここでは面積比に着目し、

$$\begin{align*}&(△AEDの面積):(△BECの面積)=a^2:(1+\sqrt{5})^2\\&=x・ED・\dfrac{1}{2} \sin ∠AED:BE・(2\sqrt{2}-x)・\dfrac{1}{2} \sin ∠BEC\\&=x・\dfrac{bx}{2}:\dfrac{2(2\sqrt{2}-x)^2}{b}\end{align*}$$

したがって、

$$a^2・\dfrac{2(2\sqrt{2}-x)^2}{b}=(1+\sqrt{5})^2・\dfrac{bx^2}{2}$$

$a=2bを用いてbを消去し、0<x<2\sqrt{2}$より、

$$\dfrac{4}{1+\sqrt{5}}=\dfrac{x}{2\sqrt{2}-x}$$

したがって、

$$x=\dfrac{8\sqrt{2}}{5+\sqrt{5}}$$

ようやく答えにたどり着きました...どうして具体的な$a,b$の値を求めなかったかわたっていただけたと思います

このような、「その値が何なのか分からなくても、結局経由するだけだから別にどうでもいい」みたいなことはまぁまぁ散見されますし、このやり方は時短にもつながるので頭の片隅に入れておくことをお奨めします！！

また何かございましたら、返信の欄にお訊きください