電流計・電圧計の仕組み，内部抵抗，分流器

電流計の仕組み

電流計は，電流が磁場から力を受ける仕組みを利用し，電流の大きさと向きを測定する装置です。回路図では以下のように図示します。

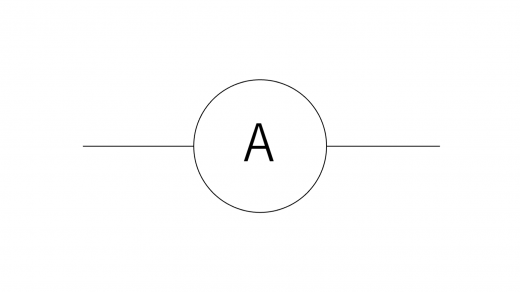
電流計は内部抵抗を持っています。理想的な場合には，後述するように，この内部抵抗は0と見なすことができます。

電流計の接続の仕方

ここでは，以下のように電流計の内部抵抗の値を明記します。

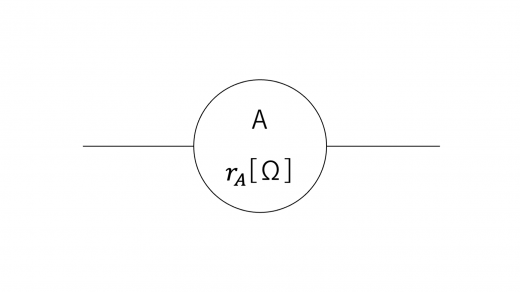
以下のような回路の抵抗に流れる電流の大きさを測定することを考えます。

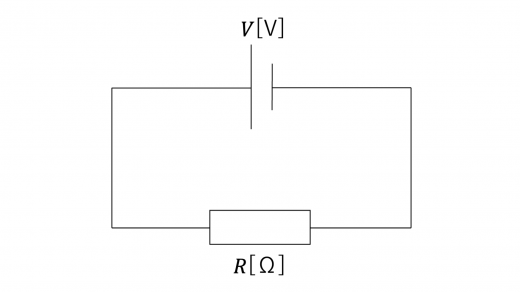
理想的な場合，上図の回路の抵抗に流れる電流 $I_0$ は

$$I_0 = \dfrac{V}{R}$$

となります。

電流計は測りたい電流が流れる抵抗と直列に接続します。

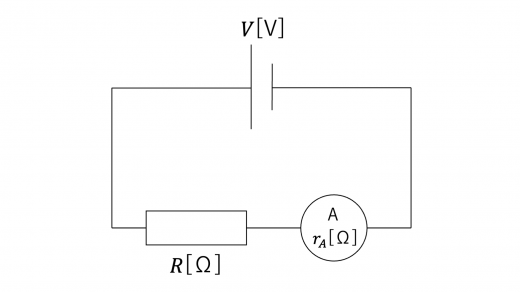
このとき，電流計が示す数値 $I_A$ は，回路全体に流れる電流の値と同じであり，合成抵抗の公式 (抵抗の直列・並列接続) を利用して

$$V = (R + r_A) I_A$$

$$\therefore I_A = \dfrac{V}{R + r_A}$$

と求められます。

電流計の内部抵抗 $r_A$ を小さくすればするほど，$I_A$ は理想値 $I_0$ に近づいていきます。このため，電流計の内部抵抗は小さければ小さい方が望ましく，理想的な場合では0と考えてよいというわけです。

実際の問題では，特に明記されない場合，電流計の内部抵抗は0として扱ってよいです。

最大測定範囲と分流器

分流器とは，電流計の最大測定範囲を拡大するために，電流計に並列に接続する抵抗のことです。

大きさ $I_1$ までの電流を測定できる電流計の測定範囲を $n (\geq 2)$ 倍に拡大することを考えます。このとき，接続する分流器の抵抗 $R^A_n$ を求めてみます。

以下のように，内部抵抗 $r_A$ の電流計に，抵抗値 $R^A_n$ の分流器を並列に接続することを考えます。このとき，これらは合わせて1つの電流計としてはたらきます。

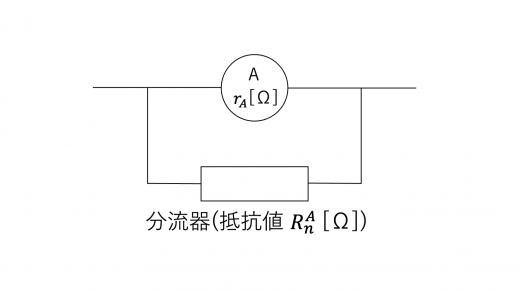
いま，この電流計に大きさ $n I_1$ の電流が流れてきたとします。このとき，元の電流計は大きさ $I_1$ までしか測定できないため，大きさ $I_1$ の電流が流れます。キルヒホッフの第1法則 (キルヒホッフの法則の解説と例題) より，分流器には大きさ $(n-1) I_1$ の電流が流れます。

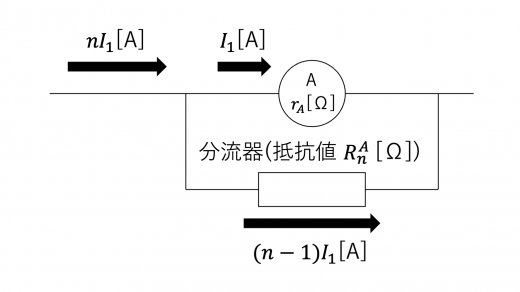
キルヒホッフの第2法則より

$$r_A I_1 = R^A_n (n-1) I_1$$

$$\therefore R^A_n = \dfrac{r_A}{n - 1}$$

と求めることができます。

例えば，最大測定範囲を10倍にしたいときは，抵抗値 $R^A_{10} = r_A /(10-1) = r_A / 9$ の分流器を用意すればよいということになります。

普段使っている電流計にはこの分流器の仕組みが使われており，さまざまな測定範囲で電流を測ることが可能になっています。

電圧計の仕組み

電圧計も，仕組みは電流計同様，電流が磁場から力を受ける仕組みを利用しています。電圧計も内部抵抗を持っており，電圧計に流れる電流を，オームの法則を用いて電圧に変換して表示しています。

電圧計は，回路図では以下のように表示します。

理想的な場合には，後述するように，電圧計の内部抵抗は十分に大きいと見なすことができます。

電圧計の接続の仕方

ここでは，以下のように電圧計の内部抵抗の値を明記します。

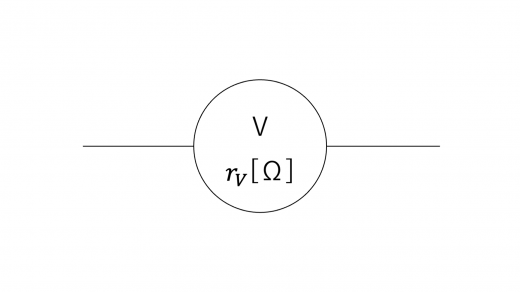
以下のような回路を構成し，抵抗値 $R_1$ の抵抗に加わっている電圧の大きさを測定することを考えます。

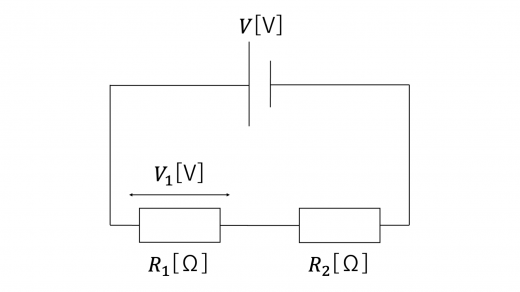
理想的な場合，加わっている電圧の大きさ $V_0$ は，キルヒホッフの法則より

$$V_0 = \dfrac{R_1}{R_1 + R_2} V$$

と予想することができます。

電圧計は測りたい対象の抵抗と並列に接続します。

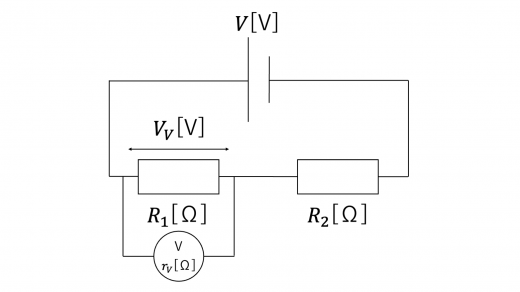
このとき，電圧計が示す数値 $V_V$ を考えます。抵抗値 $R_1$ の抵抗および電圧計に流れる電流をそれぞれ $I, i$ とすると，キルヒホッフの第1・第2法則より

$$R_1 I = r_V i$$

これらより $I, i$ について解くと

$$I = \dfrac{r_V}{R_1 r_V + R_2 r_V + R_1 R_2} V, i = \dfrac{R_1}{R_1 r_V + R_2 r_V + R_1 R_2} V$$

したがって，電圧計が測る電圧 $V_V$ は

$$V_V = r_V i = \dfrac{R_1 r_V}{R_1 r_V + R_2 r_V + R_1 R_2} V = \dfrac{R_1}{R_1 + R_2 + \dfrac{R_1 R_2}{r_V}} V$$

ここで，$r_V$ を大きくすればするほど，$V_V$ は理想値 $V_0$ に近づいていきます。このため，電圧計の内部抵抗は大きければ大きい方が望ましく，理想的な場合では(無限大とみなせるほど)十分大きいと考えてよいというわけです。

実際の問題では，特に明記されない場合，電圧計の内部抵抗は(無限大とみなせるほど)十分な大きさだとして扱ってよいです。

最大測定範囲と倍率器

倍率器とは，電圧計の最大測定範囲を拡大するために，電圧計に直列に接続する抵抗のことです。

大きさ $V_1$ までの電圧を測定できる電流計の測定範囲を $n(\geq 2)$ 倍に拡大することを考えます。このとき，接続する倍率器の抵抗 $r_n$ を求めてみましょう。

まず，以下のように電圧計を取り付けたとき，電圧計の最大測定範囲が $V_1$ であったとします。

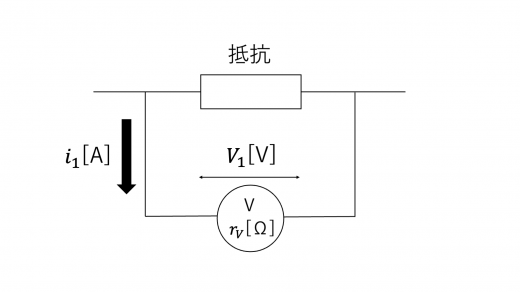
このとき，電圧計に流れる電流 $i_1$ は，電圧降下の式より

$$r_V i_1 = V_1$$

$$\therefore i_1 = \dfrac{V_1}{r_V}$$

と求められます。電圧計の元々の仕組みは電流計と同じなので，元の電圧計に流してよい最大の電流は $i_1$ となります。

さて，この電圧計の最大測定範囲を $n(\geq 2)$ 倍にするため，以下の回路のように，電圧計に抵抗値 $R^V_n$ の倍率器を取り付けることを考えます。

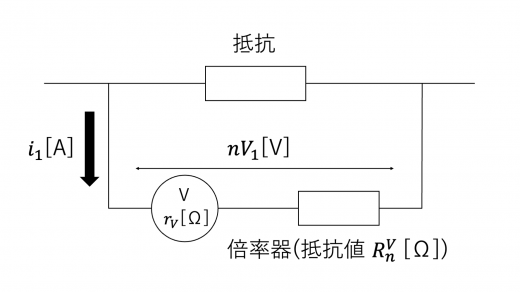
上で求めたように，この電圧計に流すことができる電流の最大値は $i_1$ なので，電圧計には電流 $i_1$ が流れます。オームの法則 (オームの法則と抵抗の性質) より

$$r_V i_1 + R^V_n i_1 = V_1 + \dfrac{R^V_n}{r_V} V_1 = n V_1$$

$$\therefore \dfrac{R^V_n}{r_V} V_1 = (n-1) V_1$$

$$\therefore R^V_n = (n-1) r_V$$

と求めることができました。

例えば，最大測定範囲を10倍にしたいときは，抵抗値 $R^V_10 = (10-1) r_V = 9 r_V$ の倍率器を用意すればよいということがわかります。

回路内でのこれらの装置の取り扱い方をまとめておきましょう。

また，電池の内部抵抗 に電流計・電圧計を用いた回路の例題が載っております。こちらも併せてご覧ください。