抵抗の直列・並列接続

回路内に複数の抵抗が接続されているとき，その抵抗が1つの抵抗であるとみなして，問題を解くことができます。このときの抵抗値を，合成抵抗 と呼びます。

抵抗が2つの場合

下図左(S1)のように，電圧 $V$ の電源に，抵抗値 $R_1$，$R_2$ の2つの抵抗を直列に接続することを考えます。

上図右の回路(S2)のように，2つの抵抗を1つとみなしたときの合成抵抗を $R_s$ とします。上図左の回路(S1)において，回路内を流れる電流が $I$ であるとすると，キルヒホッフ第2法則 (詳しくは キルヒホッフの法則の解説と例題) より

$$V = R_1 I + R_2 I = (R_1 + R_2) I \tag{1}$$

同様に，上図右の回路(S2)において，キルヒホッフ第2法則より

$$V = R_s I \tag{2}$$

(1)，(2)式を比較して

$$R_s = R_1 + R_2$$

と計算することができます。

抵抗がn個の場合

抵抗が3個の場合を考えてみましょう。下図のように，電圧 $V$ の電源に，抵抗値 $R_1, R_2, R_3$ の3個の抵抗を直列に接続することを考えます。

まず，図(S3)の赤線内の，抵抗値 $R_1, R_2$ の2つの抵抗を1つとみなした場合の合成抵抗 $R'$ を求めます。前述の公式より $R'$ は

$$R' = R_1 + R_2$$

と求められます。

次に，図(S3)の青線内の，抵抗値 $R', R_3$ の2つの抵抗を1つとみなした場合の合成抵抗 $R_{s,3}$ を求めます。これが全体の合成抵抗となります。同様に公式を用いて，$R_{s,3}$ は

$$R_{s,3} = R' + R_3 = R_1 + R_2 + R_3$$

と求めることができます。

より一般に，抵抗が $n$ 個の場合を考えます。いま，抵抗値 $R_1, R_2, ... , R_n$ のn個の抵抗を直列に接続することを考えます。これらの合成抵抗 $R_{s,n}$ は，上の議論を繰り返すことで (数学的帰納法からと言ってもよい → 数学的帰納法をわかりやすく【例題3問、応用5パターン】)

$$R_{s,n} = R_1 + R_2 + ... + R_n = \sum_{i = 1}^n R_i$$

と求められることがわかります。

抵抗が2つの場合

下図のように，電圧 $V$ の電源に，抵抗値 $R_1$，$R_2$ の2つの抵抗を並列に接続することを考えます。

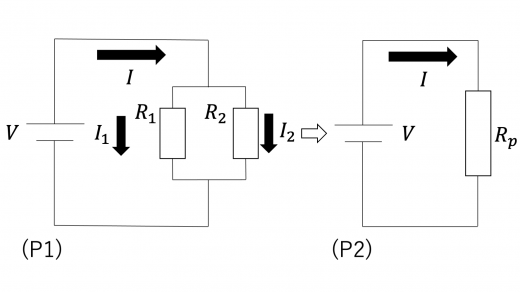
2つの抵抗を1つとみなしたときの合成抵抗を $R_p$ とします。上図左の回路において，回路全体を流れる電流が $I$，抵抗値 $R_1, R_2$ の抵抗に流れる電流がそれぞれ $I_1, I_2$ であるとします。電流に関して，キルヒホッフ第1法則 (詳しくは キルヒホッフの法則の解説と例題) より

$$I = I_1 + I_2 \tag{3}$$

また，電圧に関して，キルヒホッフ第2法則より

$$V = R_1 I_1 = R_2 I_2$$

$$\therefore I_1 = \dfrac{V}{R_1}, I_2 = \dfrac{V}{R_2} \tag{4}$$

また，上図右の回路において，キルヒホッフ第2法則より

$$V = R_p I \tag{5}$$

(3)，(4)式より，

$$I = \dfrac{V}{R_1} + \dfrac{V}{R_2} = V \left( \dfrac{1}{R_1} + \dfrac{1}{R_2} \right) \tag{6}$$

一方，(5)式より

$$I = V \dfrac{1}{R_p} \tag{5'}$$

(5’)，(6)式を比較して，合成抵抗 $R_p$ は

$$\dfrac{1}{R_p} = \left( \dfrac{1}{R_1} + \dfrac{1}{R_2} \right)$$

$$R_p = \dfrac{1}{\dfrac{1}{R_1} + \dfrac{1}{R_2}} = \dfrac{R_1 R_2 }{R_1 + R_2 }$$

と求められます。

抵抗がn個の場合

まず，抵抗が3個の場合を考えます。下図のように，電圧 $V$ の電源に，抵抗値 $R_1, R_2, R_3$ の3個の抵抗を並列に接続することを考えます。

まず，図(P3)の赤線内の，抵抗値 $R_1, R_2$ の2つの抵抗を1つとみなした場合の合成抵抗 $R''$ を求めます。公式より $R''$ は

$$\dfrac{1}{R''} = \dfrac{1}{R_1} + \dfrac{1}{R_2}$$

$$\therefore R'' = \dfrac{1}{\dfrac{1}{R_1} + \dfrac{1}{R_2}}$$

次に，図(P3)の青線内の，抵抗値 $R''$，$R_3$ の2つの抵抗を1つとみなしたときの合成抵抗 $R_{p,3}$ を求めます。この合成抵抗が，回路全体の合成抵抗となります。公式より同様に，$R_{p,3}$ は

$$\begin{aligned} \dfrac{1}{R_{p,3}} &= \dfrac{1}{R''} + \dfrac{1}{R_3} \\ &= \dfrac{1}{R_1} + \dfrac{1}{R_2} + \dfrac{1}{R_3} \end{aligned}$$

$$\therefore R_{p,3} = \dfrac{1}{\dfrac{1}{R_1} + \dfrac{1}{R_2} + \dfrac{1}{R_3}}$$

と求めることができます。

より一般に，n個の抵抗を並列に接続する場合を考えます。いま，抵抗値 $R_1, R_2, ... , R_n$ のn個の抵抗を並列に接続することを考えます。これらの合成抵抗 $R_{p,n}$ は，上の議論を繰り返すことで(あるいは数学的帰納法より)

$$\dfrac{1}{R_{p,n}} = \dfrac{1}{R_1} + \dfrac{1}{R_2} + ... + \dfrac{1}{R_n} = \sum_{k = 1}^n \dfrac{1}{R_k}$$

$$\therefore R_{p,n} = \dfrac{1}{\displaystyle \sum_{k = 1}^n \dfrac{1}{R_k}}$$

と求めることができます。

電球を直列/並列接続した場合に，回路全体の消費電力にどのような差が出るか，消費電力の観点から考察していきましょう。

電圧 $V$ の電源に，抵抗値 $R$ の2つの電球を直列または並列に接続することを考えます。

直列回路の場合，回路全体の合成抵抗 $R_a$ は，公式より

$$R_a = R + R = 2R$$

これより，回路に流れる電流は，オームの法則より

$$I_a = \dfrac{V}{R_a} = \dfrac{1}{2} \dfrac{V}{R}$$

これより，電球1つで消費されている電力 $W_a$ は

$$W = R I_a^2 = R \dfrac{1}{4} \left( \dfrac{V}{R} \right)^2 = \dfrac{1}{4} \dfrac{V^2}{R}$$

並列回路の場合，電球1つに流れる電流は，キルヒホッフの法則より

$$I_b = \dfrac{V}{R} 2 I_a$$

これより，電球1つで消費されている電力 $W_b$ は

$$W_b = R I_b = 4 R I_a^2 = \dfrac{V^2}{R}$$

したがって，電球1つあたりが消費する電力は，直列回路より並列回路の方が大きいことがわかります。つまり並列回路の電球のほうが明るいということになります。

例題を通して，合成抵抗の求め方にふれておきましょう。

全ての抵抗に流れる電流を変数としておいて，キルヒホッフの法則から愚直に求めることもできます。ここでは一貫して，抵抗全体の合成抵抗を求める解き方で解きます。

(1)回路は以下のものと等価になります。

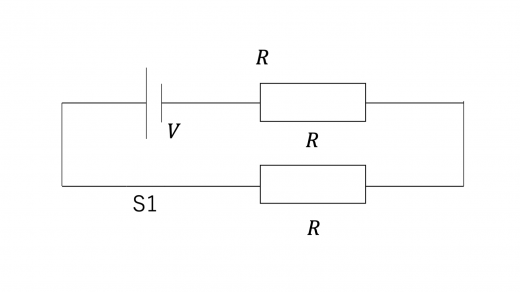
これは，抵抗値 $R$ の2つの抵抗を直列につないだ回路となります。この回路の合成抵抗 $R_1$ は，公式より

$$R_1 = R + R = 2R$$

したがって，電源から流れる電流 $I_1$ は，オームの法則より

$$I_1 = \dfrac{V}{R_1} = \dfrac{1}{2} \dfrac{V}{R}$$

となります。

(2)回路は以下のようになります。

これは以下の回路と等価になっています。

まず，並行につながっている抵抗の合成抵抗 $R'$ を求めます。これは，公式より

$$\dfrac{1}{R'} = \dfrac{1}{R} + \dfrac{1}{R} = \dfrac{2}{R}$$

$$\therefore R' = \dfrac{R}{2}$$

次に，抵抗値 $R' = R/2$，$R$ の2つの回路が直列につながっているとして，回路全体の合成抵抗 $R_2$ を求めます。公式より

$$R_2 = R' + R = \dfrac{R}{2} + R = \dfrac{3}{2} R$$

したがって，電源から流れる電流 $I_2$ は

$$I_2 = \dfrac{V}{R_2} = \dfrac{2}{3} \dfrac{V}{R}$$

のように計算することができます。