運動量保存則の例題
この記事では,運動量保存則について軽く説明した後,運動量保存の法則を用いる種々の例題を解説します。いろいろなタイプの問題を通して,運動量保存の法則に慣れることが目標です。
運動量保存則
運動量保存則
運動量保存則とは,運動方程式から導かれる以下の法則のことです。
外力がない系について,以下が成り立つ。
運動量保存則の導出や,運動量と力積との関係は,以下の記事で詳しく解説されているので,参考にしてください。
力積と運動量の関係
運動量保存則が成り立つ代表的な現象は以下ような種類があります。
- 衝突
- 合体
- 貫通
- 分裂
これらの現象は,系に外力がはたらかないので,運動量保存則の適用条件を満たしていることがわかります。
以下で実際にこれらの現象に関する例題を解き,運動量保存則に対する理解を深めましょう。
この記事に関連するQ&A
運動量保存の法則〜衝突〜
運動量保存の法則〜衝突〜
1次元を動く質点1が,速度 で,静止していた質点2に衝突した。衝突後の質点1,2の速度, をそれぞれ求めよ。ただし,質点1,2の質量は互いに等しいとし,反発係数を とする。


衝突の関係式より, また,運動量保存の法則より, 2式を解いて, を得る。
衝突を考えるときは,衝突の関係式と,運動量保存の法則を連立して解くのが定石になります。
運動量保存の法則〜合体と貫通〜
運動量保存の法則〜合体と貫通〜
以下のような均質な素材でできたブロックがなめらかな床の上に置かれている。ブロックに弾丸を速さ で打ち込んだ。弾丸に対するブロックの抵抗力を とする。また,ブロック,弾丸の質量をそれぞれ ,ブロックの横方向の厚さを とする。
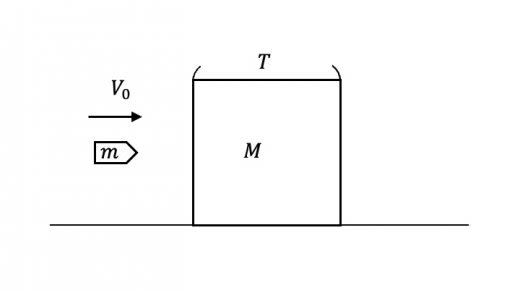 (1)弾丸はブロックにめり込み,やがてブロックに対して静止した。このとき,ブロックと弾丸が合体した系の速さを求めよ。
(1)弾丸はブロックにめり込み,やがてブロックに対して静止した。このとき,ブロックと弾丸が合体した系の速さを求めよ。
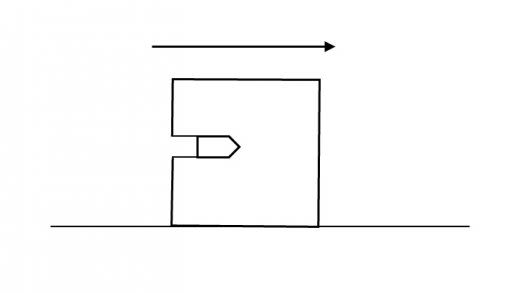 (2)弾丸は,ブロックを貫通した。このとき の下限を求めよ。また,貫通直後の弾丸の速さを求めよ。
(2)弾丸は,ブロックを貫通した。このとき の下限を求めよ。また,貫通直後の弾丸の速さを求めよ。

(1)求める速さを とする。ブロックと弾丸からなる系には外力がはたらいておらず,運動量保存の法則を用いることができる。 となる。
(2)弾丸がめり込む距離を として, となる条件を求めればよい。弾丸を打ち込むと,ブロックも動いてしまうので,相対運動を議論する必要がある。ここでは仕事とエネルギーの関係を用いる。
弾丸がブロックに だけめり込んで静止したとき,相対速度は であることに注意して, 相対運動エネルギー変化と仕事の関係を書くと以下のようになる。 ここで換算質量 を用いている。これを について整理すると, よって,これを について解いて, となる。(他にもブロックや弾丸にの運動方程式を立てて解く方法や,重心系の議論を用いる方法,v-tグラフを書く方法で解くことができる。)
運動量保存の法則〜分裂〜
運動量保存の法則〜分裂〜
上の運動量保存の法則においては,運動量を とと表現しましたが,一般に運動量はこの形であるとは限りません。例えば,原子の世界では光子1個の運動量は
と表されます。ここで はプランク定数, は光の速度, と はそれぞれ光の振動数と波長です。
このように運動量の表式が であるとき以外でも,運動量保存則は成り立ちます。
では,運動量保存則を用いて,粒子が分裂(崩壊)する現象を考えてみましょう。
電子と陽電子の質量を ,光速を とする。
(1)1次元平面上で陽電子と,運動エネルギーが の電子が対消滅
して2個の光子となり,そのうち1つは電子の進行方向と直角方向に進んだ。2つの光子の進行方向の関係を求めよ。ただし光子はほぼ逆向きに進んだとして,適当に近似をほどこしてよい。
(2)陽電子と電子が対消滅して,1個だけの光子になることはない。その理由を述べよ。
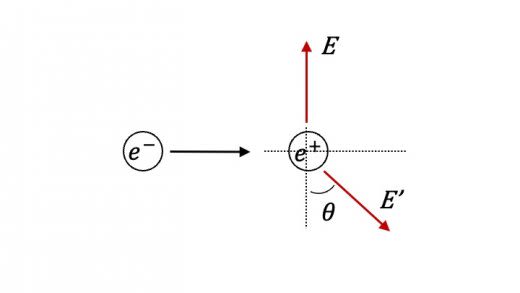 (1)直角に進んだ光子の持つエネルギーを ,もう一方の光子の持つエネルギーを とする。また,上の図ように を設定する。
(1)直角に進んだ光子の持つエネルギーを ,もう一方の光子の持つエネルギーを とする。また,上の図ように を設定する。
エネルギー保存より,
運動量保存より,
1式目は水平方向,2式目は直角方向の運動量保存の式である。
これら2式と,光子がほぼ逆向きに進んだ()という仮定より, としてよい。
運動量保存の2式の2乗和をとって,
これとエネルギー保存の式より,
となる。
運動量保存の式を辺々わることで,
を得る。
(2)陽電子と電子の重心系で見ると,これらはお互い逆向き同じ大きさで動くので,系の全運動量は である。しかし,対消滅後光子がただ1つ生じたとすると,その運動量は となり,これは決して となりえないので矛盾が生じる。
光子の運動量を考える代表例題として,高校範囲ではCompton散乱があります。以下の記事では,光子の運動量やエネルギーの扱いと,Compton散乱が詳しく解説されています。
コンプトン効果/散乱における波長の伸びの導出過程
補足 対消滅
世の中には,反物質という物質の対になる粒子が存在することが知られています。例えば,陽子の反物質は陽電子,電子ニュートリノの反物質は反電子ニュートリノです。
物質と反物質が衝突すると,それらが消滅してしまい,エネルギーをもった異なる粒子(例題中では光子)に変換されることがわかっています。このような現象のことを対消滅といいます。
対消滅で粒子が文字通り消滅してしまうのは面白いですね。











