エントロピーの定義とエントロピー増大の法則の意味

熱力学第二法則のトムソンの原理「熱源から熱を受け取り，それを全て仕事に変えるような熱サイクルは存在しない。」について数式で表すことを考えます。

まず，任意の熱効率 $\eta$ とカルノーサイクルの熱効率 $\eta_c$ には次のように表現できます。

$$\begin{aligned} \eta &= 1-\dfrac{|Q_2|}{Q_1} \\ \eta_c &= 1-\dfrac{T_2}{T_1} \\ \end{aligned}$$

カルノーの定理より，２つの式には次のような関係があります。

$$\eta \leq \eta_c$$

順サイクル（高熱源から低熱源に熱を放出する過程）では，$Q_1>0$，$Q_2 < 0$ を考慮に入れて，カルノーの定理に代入すると，

$$1+\dfrac{Q_2}{Q_1} \leq 1-\dfrac{T_2}{T_1}$$

$Q_1>0$，$T_2>0$ より，

$$\begin{aligned} \dfrac{Q_2}{T_1} + \dfrac{Q_2}{T_1} \leq 0 \\ \end{aligned}$$

となります。可逆サイクルのときに等号が成立し，不可逆サイクルのときは不等号が成立します。

上記の式は熱源が２つの場合の関係式です。この熱源を $n$ 個 $( n \geq 0 )$ に増やし，熱源 $R_i (i = 0，1，2，\dots ，n)$ (各温度 $T_i$) について考えます。

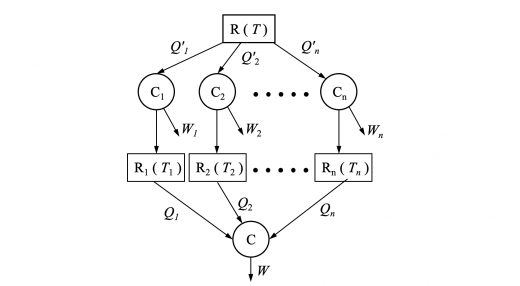
n個の熱サイクルでは，

1. 可逆サイクル $C_i$ は温度 $T$ の熱源 $R$ から熱 $Q_i'$ を吸収します。

2. 可逆サイクル $C_i$ は外部に仕事 $W_i$ をし，残りの熱 $-Q_i$ を各熱源　$R_i$　に放出します。

3. 任意のサイクル $C$ は各熱源 $R_i$ から熱 $Q_i$ を吸収し，外部に仕事 $W$ をします。

任意のサイクル $C$ について熱力学第一法則より，

$$\sum_i Q_i + W = 0$$

また，各サイクル $C_i$ について熱力学第一法則より，

$$\begin{aligned} Q_i' - Q_i + W_i =0 \\ (i = 1，2，\dots ，n) \\ \end{aligned}$$

$n$ 個の式の辺々を足し合わせると，

$$\begin{aligned} \sum_i Q_i' + W + \sum_i W_i = 0 \\ \sum_i Q_i' = - \Bigl (W + \sum_i W_i \Bigr)\\ \end{aligned}$$

となります。

ここで，$C$　と　$\sum_i C_i$ を足し合わせた大きなサイクルについて考えます。

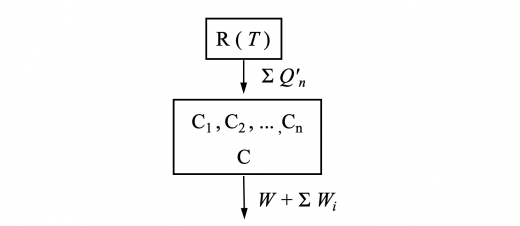
もし，$\sum_i Q_i' > 0$ だとすると，熱源 $R$ から熱 $\sum_i Q_i'$ を受け取り，すべての熱を仕事　$\bigl (W + \sum_i W_i \bigr)$ に100%変換していることになっています。

これは熱力学第二法則のトムソンの原理「熱源から熱を受け取り，それを全て仕事に変えるような熱サイクルは存在しない。」に反します。

したがって， $$\sum_i Q_i' \leq 0$$

でなければいけません。これは外部から仕事した全てを熱として熱源 $R$ に戻すことを意味しています。

一方，$C_i$ は可逆サイクルのため，

$$\begin{aligned} \dfrac{Q_i'}{T} + \dfrac{-Q_i}{T_i} =0 \\ (i = 1，2，\dots ，n) \\ \end{aligned}$$

が成立し，$n$ 個の式を考えると，

$$\begin{aligned} \dfrac{1}{T} \sum_i Q_i' - \sum_i \dfrac{Q_i}{T_i} =0 \\ \sum_i \dfrac{Q_i}{T_i} = \dfrac{1}{T} \sum_i Q_i' \\ \end{aligned}$$

$\sum_i Q_i' \leq 0$ より，

$$\sum_i \dfrac{Q_i}{T_i} \leq 0$$

という式を導くことができます。等号は可逆変化の場合，不等号は不可逆変化の場合で成立します。この式を温度 $T$ の微小部分から熱 $\delta Q$ を吸収すると考え積分系に直すと，

$$\oint \dfrac{\delta Q}{T} \leq 0$$

となります。これをクラウジウスの不等式といい，熱力学第二法則を数式化したものと考えられます。積分記号 $\oint$ は1サイクルについて積分することを表しています。

図のようなp-vグラフにおける状態 $\mathrm{O}$ と状態 $\mathrm{A}$ に関する状態変化について考えます。過程 $\mathrm{O} \to \mathrm{C} \to \mathrm{O}$ と過程 $\mathrm{O} \to \mathrm{C'} \to \mathrm{O}$ の二種類考えられ，どちらも可逆過程です。

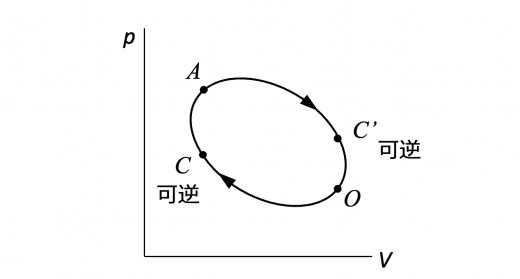
式で表現すると，

$$\oint \dfrac{\delta Q}{T} = \int_{O(C)}^A \dfrac{\delta Q}{T} + \int_{A(C')}^O \dfrac{\delta Q}{T} =0$$

となります。過程$\mathrm{O} \to \mathrm{C} \to \mathrm{O}$ と過程$\mathrm{O} \to \mathrm{C'} \to \mathrm{O}$ は逆の経路のため，

$$\int_{A(C')}^O \dfrac{\delta Q}{T} = - \int_{O(C')}^A \dfrac{\delta Q}{T}$$

が成り立ちます。上の式と組み合わせて，

$$\begin{aligned} \int_{O(C)}^A \dfrac{\delta Q}{T} - \int_{O(C')}^A \dfrac{\delta Q}{T} &= 0 \\ \int_{O(C)}^A \dfrac{\delta Q}{T} = \int_{O(C')}^A \dfrac{\delta Q}{T} \end{aligned}$$

となります。

したがって，$\int_{O}^A \dfrac{\delta Q}{T}$ は経路に依存せず，状態 $\mathrm{O}$ と状態 $\mathrm{A}$ のみで決まるため状態量となります。クラウジウスはこれを新しい状態量としてエントロピーと定義しました。

エントロピーの微小変化 $dS$ は，

$$dS = \dfrac{\delta Q}{T}$$

となり，

$$\delta Q = T dS$$

と書き直すことができます。よって，エントロピー $S$ を用いることで，非状態量である熱 $Q$ を状態量を使って表現できるようになりました。エントロピーの単位は$\mathrm{J K^{-1}}$ で表されます。

さらに，熱力学第一法則はエントロピーを用いて，

$$dU = TdS - p dV$$

と書き直すことも可能です。

エントロピーの記号 $S$ について

エントロピーの記号に $S$ を用いることに，違和感を覚えた方もいるのではないでしょうか？

記号 $S$は，フランスの物理学者サディ・カルノー（1796-1832）の頭文字にあたります。カルノーは「カルノーサイクル」の研究で熱力学の発展に大きく貢献しています。

ただし，エントロピーを定義したのはドイツの物理学者ルドルフ・クラウジウス（1822-1888）です。

状態量のエントロピーが持つ物理的な意味は，「エントロピー増大の法則」が示しています。ここではエントロピー増大の法則について解説していきます。

状態Xから状態Yへの不可逆過程（Irrev）と，状態Yから状態Xへの可逆過程(Rev)を考えます。クラウジウスの不等式 $\oint \dfrac{\delta Q}{T} \leq 0$ について考えると，

$$\begin{aligned} \oint \dfrac{\delta Q}{T} &= \int_{X(Irrev)}^Y \dfrac{\delta Q}{T} + \int_{Y(Rev)}^X \dfrac{\delta Q}{T} \\ &= \int_{X(Irrev)}^Y \dfrac{\delta Q}{T} + \{ S(X)- S(Y)\} \lt 0 \\ \end{aligned}$$

$$S(Y)-S(X) \gt \int_{X(Irrev)}^Y \dfrac{\delta Q}{T}$$

となります。不可逆過程を含むので不等号のみ成立します。可逆過程の場合は等号が成立します。エントロピーの微小変化 $dS$に関して,

$$dS \gt \dfrac{\delta Q}{T}$$

となります。ここで，状態Xから状態Yへ断熱過程の場合を考えると $\delta Q =0$ が成立します。

$$dS \gt \dfrac{\delta Q}{T} = 0$$

したがって,　不可逆断熱過程ではエントロピーは増大します。可逆過程では等号が成立します。これをエントロピー増大の法則といいます。

不可逆変化はエントロピーが増大する方向と一致し，熱平衡状態（安定状態）はエントロピーが最大の状態となります。

宇宙の膨張とエントロピー増大則

余談ですが，宇宙全体を孤立系（断熱系）と考えると，「エントロピー増大の法則」が成り立ち，宇宙のエントロピーは増大し続けます。

理論的には最終的にエントロピーが最大化し，宇宙が熱平衡状態に達します。すると，宇宙の温度が均一化され生命活動が維持できなくなります。この状態は「宇宙の熱的死」といわれています。

エントロピー変化の例題

エントロピー変化に関する例題を解いていきます。

エントロピーの概念は熱力学分野から生まれたものですが，エントロピーは統計力学において重要な役割を果たしています。エントロピーの簡単な説明に「エントロピーは"乱雑さ"を示している」というものがあります。

エントロピーが乱雑さと説明されるのは，統計力学的な解釈(確率的解釈)に基づいています。簡単な分子論モデルを使ってエントロピーや不可逆過程について考えていきます。

エントロピー増大則と確率的解釈

気体拡散におけるエントロピー変化についてに考えていきます。

状態Aでは箱を左右で区切り，左側はガス，右側は真空です。仕切りを外すと状態Aから状態Bに変化していきます。

• 状態A：ガスが左側に集まっている状態（仕切りを外した直後）
• 状態B：ガスが箱全体に充満した状態

状態A→状態Bは不可逆変化であることは直感的に理解できると思います。

上記のことを確率的に解釈すると，仕切りを外した直後の状態Aは，めったに起こり得ない特殊な状態です。ガスが自然に一部分に集まることは起きないからです。

一方，状態Bはよく起こりうる状態です。

つまり，上記の不可逆変化は確率が低い状態から，確率が高い状態に遷移することを意味しています。

熱力学において，エントロピーが増加する方向と不可逆変化は一致します。すなわち，統計力学における不可逆変化（エントロピーが増大する方向）は，低確率の状態から高確率の状態への変化といえます。

そして，確率が最大のとき，エントロピーが最大となります。

気体拡散の例から，気体分子が"乱雑"なほどエントロピーが大きく，秩序的なほどエントロピーが小さいともいえます。そのため，エントロピーを乱雑さの指標として解釈することができます。

ボルツマンの関係式の導出

上記の気体拡散の例を状態数を用いて考えてみます。状態AとBの状態数を $W_A$，$W_B$ とすると，系全体の状態数は積で表現でき，$W_A \times W_B$ となります。

また，エントロピーは示量変数で加法が成り立ち，状態AとBのエントロピーを $S_A$ ，$S_B$ とすると，系全体のエントロピーは $S_A+S_B$ と記述できます。

エントロピー $S$ は状態数 $W$ に依存する関数であり，$S$ と $W$ との間には対数を用いて，

$$S_A + S_B = k_B \log (W_A \times W_B) \\$$

が成り立ちます。したがって，エントロピー $S$ と状態数 $W$ に，

$$S = k_B \log{W}$$

という関係が導かれます。これはボルツマンの関係式といいます。この式は状態数とエントロピーを結ぶ重要な式です。 $k_B$ はボルツマン定数($k_B = 1.38 \times 10^{-38} \mathrm{J K^{-1}}$)といいます。

熱力学第三法則とエントロピー

熱力学第一法則，熱力学第二法則に続いて，熱力学第三法則も存在します。ネルンストの熱定理とも言われます。

これはボルツマンの関係式 $S = k_B \log{W}$ から導かれます。

絶対零度 $0 K$ において，分子は静止し位置が完全に決まります。そのため，微視的状態数 $W$ は1になります。このとき，エントロピー $S$ は0となります。

詳しく知りたい方は，統計力学を勉強してみてください。

エントロピーと情報理論

余談ですが，エントロピーは熱力学や統計力学だけではなく、情報理論という数学分野でも大きな役割を果たしています。

情報理論に関して興味がある方は，以下の記事を参考にしてください。

情報量の意味

相互情報量の意味とエントロピーとの関係

以上，エントロピーやエントロピー増大則の物理的な解釈を説明してきました。最後に身の回りにあるエントロピー増大則を紹介していきます。

エントロピー増大則とは不可逆過程を意味します。すなわち，自然に変化が起こる方向性がエントロピーが増大する方向と一致します。

例えば，

• 熱いコーヒーを置いておけば，自然に冷めていく。

• コーヒーにミルクを入れれば，次第に混ざってコーヒーミルクになる。

• 暖房を入れると，暖かい空気が部屋中に充満する。

これらの現象は経験的にイメージできると思います。そして，逆事象の「冷めたコーヒーを置いておくと自然に熱くなる」，「混ぜたコーヒーミルクが勝手にコーヒーとミルクに分離する」などは起こりえません。

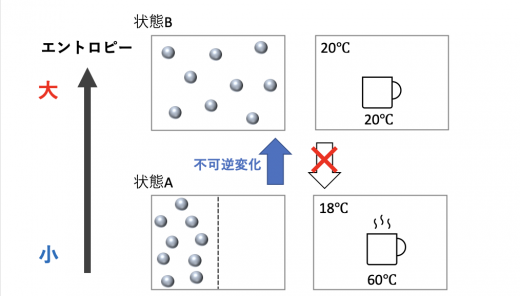
状態Aから状態Bにエントロピーが大きくなり，状態Aから状態Bへの方向性がエントロピー増大則となります。