図よりとありますが、なぜこうなるのかわかりません

放物線の $y\geqq0$ の条件がなかった場合で、放物線と直線が共有点をもつような $k$ の値の範囲を考え、その範囲で $k$ を動かしてギリギリのときに接する、というように考えれば、すぐにわかるようになると思います。

(逆に、共有点をもたない範囲のギリギリが接する直前と考えてもOK)

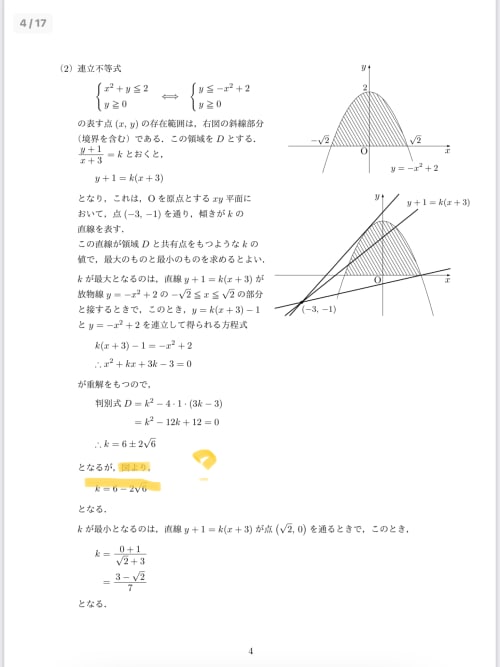
今回だと、共有点をもつときの範囲は、

$$\begin{aligned}D \geqq 0 &\iff k^2-12k+12 \geqq 0 \\&\iff k \leqq 6-2\sqrt{6} , 6+2\sqrt{6} \leqq k\end{aligned}$$

$6-2\sqrt{6}>0$ であり、傾きを $k=0$ からスタートして大きくしていったとき、最初に接するのは $k=6-2\sqrt{6}$ のときで、それが今回の答えになる値です。

$6-2\sqrt{6}$ より大きくなると共有点をもたなくなりますが、$k=6+2\sqrt{6}$ のときに $y<0$ の部分で再び接することになり、$k>6+2\sqrt{6}$ では異なる2点で共有点をもちます。

$k=6+2\sqrt{6}$ での接点の座標ですが、実際に二次方程式を解くことで得られます。

$$\begin{aligned}x^2+kx+3k-3=0 &\iff x^2+(6+2\sqrt{6})x+15+6\sqrt{6}=0 \\&\iff (x+3+\sqrt{6})^2 =0 \\&\iff x=-3-\sqrt{6}\end{aligned}$$

ちなみに、この因数分解は思いつかないよ！と思ったら、接する条件を思い出してください。接しているので必ず重解をもつ、つまり完全平方式になるはずです。

そして、$y$ についても計算することで、接点の座標は $(-3-\sqrt{6},-13-6\sqrt{6})$ となります。