【解答・解説】早稲田理工物理2025 第3問 -熱力学-
2025年度の早稲田大学基幹・創造・先進理工学部物理第3問を解説します。熱力学の単元です。
この記事に関連するQ&A
問題
問題
以下の問題文および図は,2025年度早稲田大学基幹・創造・先進理工学部入試問題物理第3問から引用しています(一部見やすさ等のためライターが修正・変更した部分があります)。
以下の問に答えよ。
図1 のような円筒容器 A と円筒容器 B,円筒形シリンダーが弁 1 の付いた管と弁 2 の付いた管で接続されている装置が鉛直に立てて置かれている。
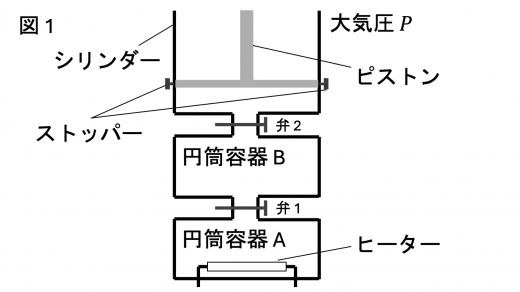
容器 A と容器 B の容積はともに であり,シリンダーの容積は である。容器 A の内部にはヒーターが取り付けられている。また,シリンダーは断面積が であり,上端が開いていて,ピストンより上の気体は常に大気圧 となっている。ヒーター以外の装置のすべては断熱材でできており,装置のすべての熱容量は無視できる。また,管と弁,ヒーターの容積や厚さは無視できる。さらに,ピストンは厚さや質量が無視でき,なめらかに動く。気体定数を ,重力加速度の大きさを とする。
最初,弁 1 と弁 2 は閉じられており,ピストンはそれより下のシリンダー内の容積が となる位置にストッパーで固定されていた。また,ヒーターのスイッチはオフであった。この状態で,容器 A には絶対温度 ,圧力 の単原子分子の理想気体 が,容器 B には絶対温度 ,圧力 の単原子分子の理想気体 が入っていた。また,ピストンより下のシリンダー内は真空であった。
問1 気体 のモル数は気体 の何倍か。
問2 気体 の内部エネルギーは気体 の内部エネルギーの何倍か。
続いて,図2 のように弁 2 を閉じたまま,弁 1 を開き気体 と気体 を混合する。
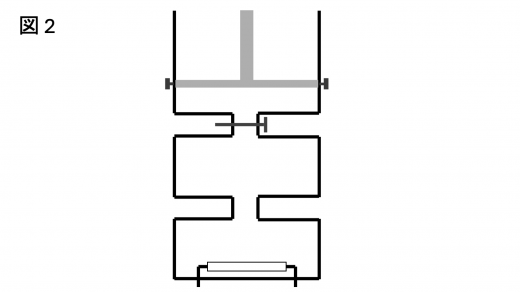
十分時間が経過し,熱平衡に達した状況を考える。ただし,2 つの気体は化学反応しないものとする。
問3 混合気体の絶対温度は の何倍か。
問4 混合気体の圧力は の何倍か。
続いて,図3 のように弁 2 も開き,混合気体をシリンダー内に膨張させた。
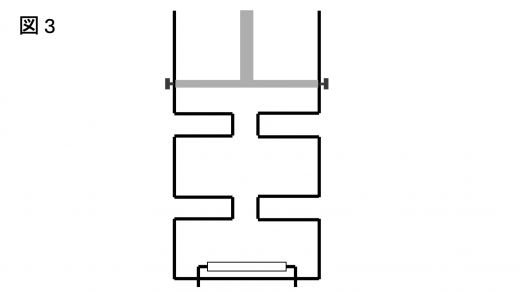
十分時間が経過し,熱平衡に達した状況を考える。
問5 混合気体の絶対温度は の何倍か。
問6 混合気体の圧力は の何倍か。
続いて,図4 のようにシリンダー内に液体をシリンダーの上端まで注いだ。その後,ピストンを固定しているストッパーをはずしたところ,ピストンは止まったままであった。
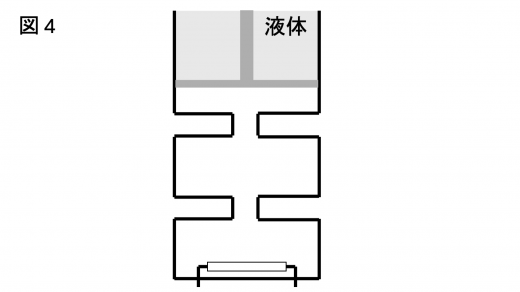
問7 液体の密度を答えよ。
この状態からヒーターのスイッチを入れ,混合気体をゆっくりと温めたところ,ピストンは徐々に上昇し,それとともに液体がシリンダーの上端からゆっくりとこぼれはじめた。
問8 シリンダーに残っている液体の体積が となった瞬間の混合気体の絶対温度は の何倍か。
問9 ピストンが上昇しはじめてから残っている液体の体積が となった瞬間までに混合気体が外部にした仕事は,最初に気体 がもっていた内部エネルギーの何倍か。
問10 ピストンが上昇しはじめてから残っている液体の体積が となった瞬間までに混合気体が吸収した熱量は,最初に気体 がもっていた内部エネルギーの何倍か。
状態変化ごとの各物理量の変化を丁寧に追うことが求められる問題です。
解答例
解答例
(1)
気体 のモル数をそれぞれ とします。各気体について状態方程式 (ボイル・シャルルの法則と状態方程式) より
辺々割って
したがって,気体 のモル数は気体 の2倍となります。
(2)
気体 はいずれも 単原子分子の理想気体なので,その内部エネルギーは公式 (気体の内部エネルギーの意味と公式,求め方) により求めることができます。各気体の内部エネルギーをそれぞれ とすると
したがって, は の4倍となります。
(3)
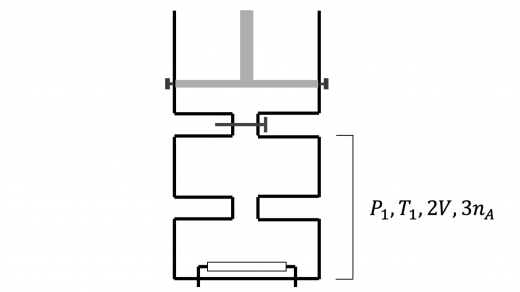
上図のように,弁 1 を開いてから十分時間が経過した後の混合気体の 圧力・温度をそれぞれ とおきます。混合気体の体積は ,総モル数は となります。 この状態変化は断熱変化 (気体の状態変化とモル比熱(断熱変化,等温変化,定圧変化など)) であり,さらに混合気体がした総仕事量も であるので,熱力学第一保存則 (熱力学第一法則|仕事と内部エネルギーの関係) より,この状態変化において混合気体の総内部エネルギーの変化 は であることがわかります。すなわち
したがって
であることがわかります。
(4)
混合気体に対する状態方程式より
(1) 式を用いて辺々割ると
となります。
(5)
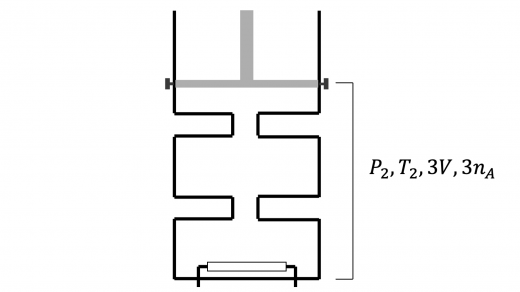
上図のように,弁 2 を開いてから十分時間が経過した後の混合気体の圧力・温度をそれぞれ とおきます。
(3) と同様の議論により,この状態変化においても内部エネルギーの変化は 0 となります。したがって
となります。
この結果より,この状態変化は等温変化となることがわかります。
(6)
(5) の結果より,この状態変化は等温変化となることがわかります。 したがって,ボイルの法則 (ボイル・シャルルの法則と状態方程式) より
と求められます。
(7)
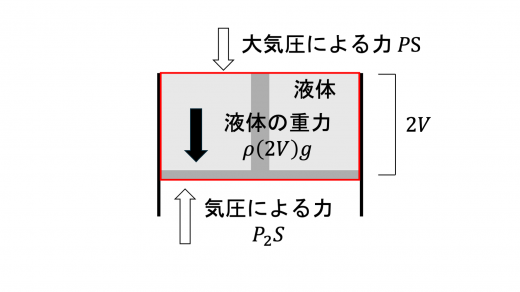
液体の密度を とおきます。液体とピストンの系に対して 力のつりあいより
となります。
(8)
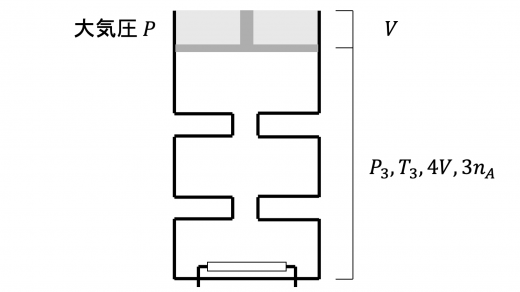
シリンダーに残っている液体の体積が となったときの 混合気体の圧力と温度をそれぞれ とおきます。 このとき気体の総体積は となっていることに注意します。
まず,圧力 について,液体とピストンの系に対する力のつりあいより
また,この気体の状態変化はボイル・シャルルの法則にしたがうので
と求めることができます。
(9)
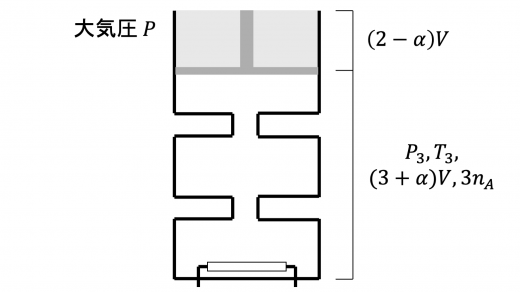
上図のように,シリンダーの最上部の気体の体積が となっているときを考えます。液体の残り体積が となるまでの状態変化を考えたいので, として考えます。
このときの気体の圧力・体積・温度をそれぞれ とおきます。まず, については
となります。次に, について,液体とピストンの系に関する力のつりあいより
これらより を消去して, と の関係式を求めると
では となるので, この状態変化で気体が外部にした仕事 は,下図の 平面の斜線部の面積と等しくなります。
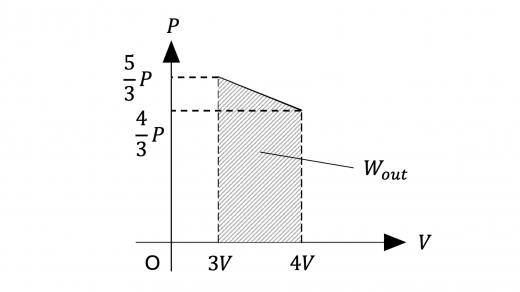
したがって, は
のように を用いて表すことができるので
となります。
(10)
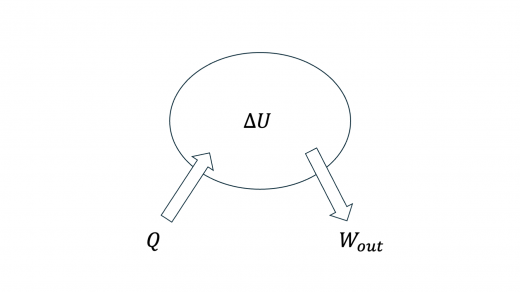
熱力学第一法則より,この状態変化の過程で気体が外部にした仕事を ,気体が吸収した仕事を とすると
は前問で求めた通りなので, を求めます。
したがって, は
と求められます。
気体の状態変化を丁寧に追うことが求められます。 グラフを描いて仕事を求める問題は入試としては珍しいかもしれません。











