I
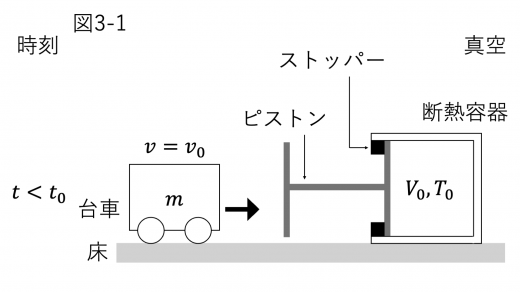
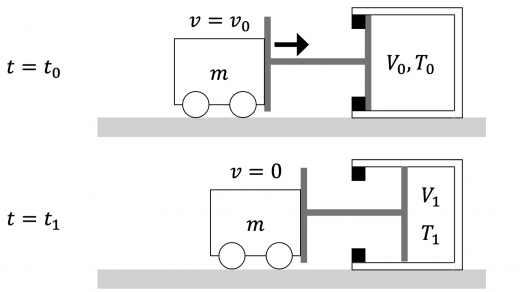
「台車と床との摩擦~は無視できる」ことと「なめらかに動くピストンつきの断熱容器」を用いていることから,系全体でエネルギー保存則が成り立つことと,断熱容器内の気体は断熱変化に従うことに注意します。
(1)
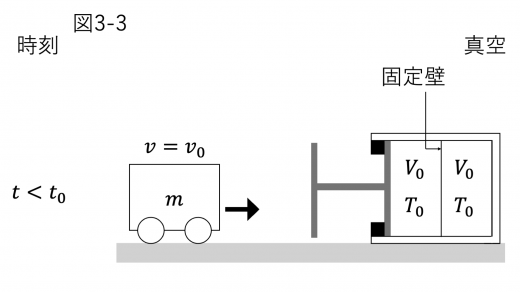
時刻 t 0 t_0 t 0 v 0 v_0 v 0
K 0 = 1 2 m v 0 2
K_0 = \dfrac{1}{2} m v_0^2
K 0 = 2 1 m v 0 2
また,単原子分子理想気体の内部エネルギーの公式より
U 0 = 3 2 R T 0
U_0 = \dfrac{3}{2} R T_0
U 0 = 2 3 R T 0
(2)
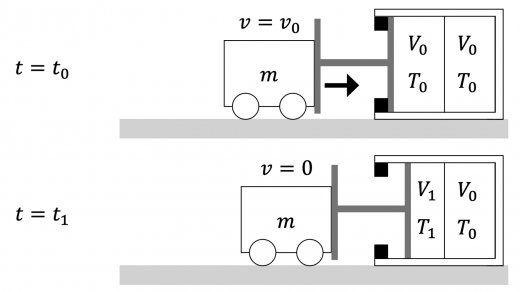
時刻 t = t 0 t = t_0 t = t 0 t = t 1 t = t_1 t = t 1
3 2 R T 1 = K 0 + U 0
\dfrac{3}{2} RT_1 = K_0 + U_0
2 3 R T 1 = K 0 + U 0
両辺を U 0 = 3 2 R T 0 U_0 = \dfrac{3}{2} R T_0 U 0 = 2 3 R T 0
T 1 T 0 = K 0 U 0 + 1
\dfrac{T_1}{T_0} = \dfrac{K_0}{U_0} + 1
T 0 T 1 = U 0 K 0 + 1
と表される。
(3)
断熱変化においては,一般に,ポアソンの法則 p V 5 / 3 = 一定 p V^{5/3} = \text{一定} p V 5/3 = 一定 p V = n R T p V = n R T p V = n RT T V 2 / 3 = 一定 T V^{2/3} = \text{一定} T V 2/3 = 一定
時刻 t = t 0 t = t_0 t = t 0 t = t 1 t = t_1 t = t 1
T 0 V 0 2 3 = T 1 V 1 2 3
T_0 V_0^{\dfrac{2}{3}} = T_1 V_1^{\dfrac{2}{3}}
T 0 V 0 3 2 = T 1 V 1 3 2
∴ ( V 1 V 0 ) 2 3 = T 0 T 1 = ( K 0 U 0 + 1 ) − 1
\therefore \left( \dfrac{V_1}{V_0} \right)^{\dfrac{2}{3}} = \dfrac{T_0}{T_1} = \left( \dfrac{K_0}{U_0} + 1 \right)^{-1}
∴ ( V 0 V 1 ) 3 2 = T 1 T 0 = ( U 0 K 0 + 1 ) − 1
∴ V 1 V 0 = ( K 0 U 0 + 1 ) − 3 2 ( < 1 )
\therefore \dfrac{V_1}{V_0} = \left( \dfrac{K_0}{U_0} + 1 \right)^{-\dfrac{3}{2}} (< 1)
∴ V 0 V 1 = ( U 0 K 0 + 1 ) − 2 3 ( < 1 )
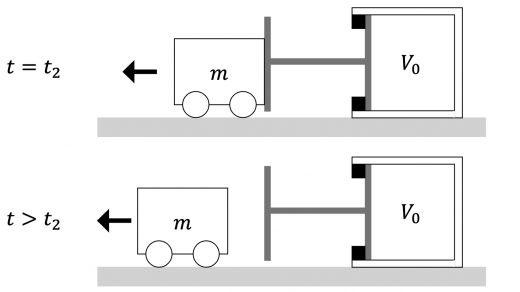
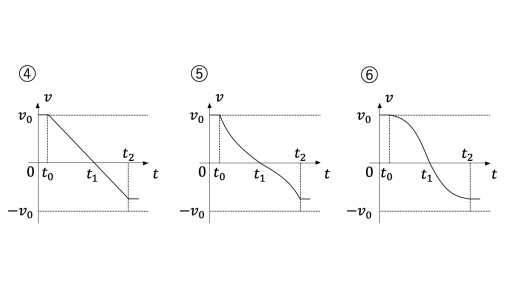
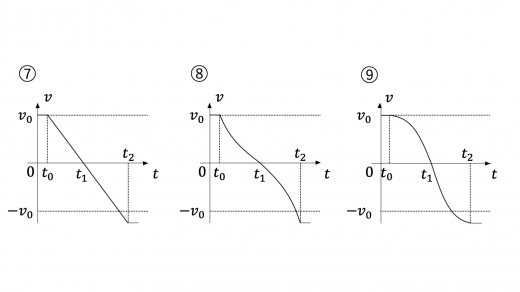
(4)まず,時刻 t = t 0 t = t_0 t = t 0 t = t 2 t = t_2 t = t 2 t = t 2 t = t_2 t = t 2 v = − v 0 v = - v_0 v = − v 0
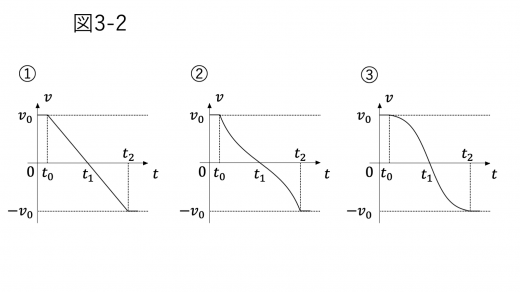
速度がどのように変化するかを考えましょう。時刻 t = t 0 t = t_0 t = t 0 t = t 1 t = t_1 t = t 1 V V V p V 5 / 3 = 一定 p V^{5/3} = \text{一定} p V 5/3 = 一定 p p p t = t 1 t = t_1 t = t 1 p p p
そこで,グラフに着目すると,t 0 ≤ t ≤ t 1 t_0 \leq t \leq t_1 t 0 ≤ t ≤ t 1 t = t 1 t = t_1 t = t 1
II
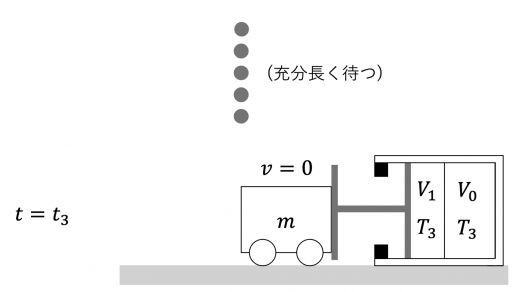
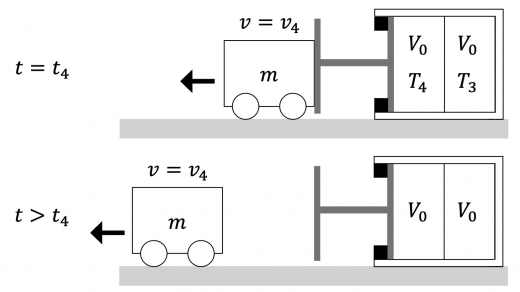
(1)「R , T 3 , T 4 R, T_3, T_4 R , T 3 , T 4
時刻 t = t 3 t = t_3 t = t 3 t = t 4 t = t_4 t = t 4
K 4 + 3 2 R T 4 = 0 + 3 2 R T 3
K_4 + \dfrac{3}{2} R T_4 = 0 + \dfrac{3}{2} R T_3
K 4 + 2 3 R T 4 = 0 + 2 3 R T 3
∴ K 4 = 3 2 R ( T 3 − T 4 )
\therefore K_4 = \dfrac{3}{2} R (T_3 - T_4)
∴ K 4 = 2 3 R ( T 3 − T 4 )
と求められます。
(2)エネルギー保存則およびポアソンの法則を用いながら,各温度間の関係を比べてみましょう。
まず T 0 T_0 T 0 T 1 T_1 T 1
時刻 t = t 0 t = t_0 t = t 0 t = t 1 t = t_1 t = t 1
T 1 V 1 2 / 3 = T 0 V 0 2 / 3
T_1 V_1^{2/3} = T_0 V_0^{2/3}
T 1 V 1 2/3 = T 0 V 0 2/3
∴ T 1 = ( V 0 V 1 ) 2 3 T 0 (2-1)
\therefore T_1 = \left( \dfrac{V_0}{V_1} \right)^{\frac{2}{3}} T_0 \tag{2-1}
∴ T 1 = ( V 1 V 0 ) 3 2 T 0 ( 2-1 )
台車の運動の方向より,V 0 V 1 > 1 \dfrac{V_0}{V_1} > 1 V 1 V 0 > 1 ( V 0 V 1 ) 2 3 > 1 \left( \dfrac{V_0}{V_1} \right)^{\frac{2}{3}} >1 ( V 1 V 0 ) 3 2 > 1
T 0 < T 1
T_0 < T_1
T 0 < T 1
であることがわかります。
次に T 3 T_3 T 3 t 1 ≤ t ≤ t 3 t_1 \leq t \leq t_3 t 1 ≤ t ≤ t 3
時刻 t = t 1 t = t_1 t = t 1 t = t 3 t = t_3 t = t 3
0 + 3 2 R T 3 + 3 2 R T 3 = 0 + 3 2 R T 1 + 3 2 R T 0
0 + \dfrac{3}{2} R T_3 + \dfrac{3}{2} R T_3 = 0 + \dfrac{3}{2} R T_1 + \dfrac{3}{2} R T_0
0 + 2 3 R T 3 + 2 3 R T 3 = 0 + 2 3 R T 1 + 2 3 R T 0
∴ T 3 = T 0 + T 1 2 (2-2)
\therefore T_3 = \dfrac{T_0 + T_1}{2} \tag{2-2}
∴ T 3 = 2 T 0 + T 1 ( 2-2 )
いま T 0 < T 1 T_0 < T_1 T 0 < T 1
T 0 < T 3 < T 1
T_0 < T_3 < T_1
T 0 < T 3 < T 1
だとわかります。
最後に T 4 T_4 T 4 t 3 ≤ t ≤ t 4 t_3 \leq t \leq t_4 t 3 ≤ t ≤ t 4
T 4 V 0 2 / 3 = T 3 V 1 2 / 3
T_4 V_0^{2/3} = T_3 V_1^{2/3}
T 4 V 0 2/3 = T 3 V 1 2/3
∴ T 4 = ( V 1 V 0 ) 2 3 T 3
\therefore T_4 = \left( \dfrac{V_1}{V_0} \right)^{\frac{2}{3}} T_3
∴ T 4 = ( V 0 V 1 ) 3 2 T 3
ここで,(2-1)式より
( V 1 V 0 ) 2 3 = T 0 T 1
\left( \dfrac{V_1}{V_0} \right)^{\frac{2}{3}} = \dfrac{T_0}{T_1}
( V 0 V 1 ) 3 2 = T 1 T 0
したがって
T 4 = T 3 T 1 T 0 < T 0 ( ∵ T 3 < T 1 ) (2-3)
T_4 = \dfrac{T_3}{T_1} T_0 < T_0 \, (\because T_3 < T_1) \tag{2-3}
T 4 = T 1 T 3 T 0 < T 0 ( ∵ T 3 < T 1 ) ( 2-3 )
全てまとめて
T 4 < T 0 < T 3 < T 1
T_4 < T_0 < T_3 < T_1
T 4 < T 0 < T 3 < T 1
のようになります。> > >
(3)
K 0 = 1 2 m v 0 2 , U 0 = 3 2 R T 0 , K 4 = 1 2 m v 4 2
K_0 = \dfrac{1}{2} m v_0^2, U_0 = \dfrac{3}{2} R T_0, K_4 = \dfrac{1}{2} m v_4^2
K 0 = 2 1 m v 0 2 , U 0 = 2 3 R T 0 , K 4 = 2 1 m v 4 2
と表されます。したがって
e 2 = ∣ v 4 v 0 ∣ 2 = K 4 K 0
e^2 = \left| \dfrac{v_4}{v_0} \right|^2 = \dfrac{K_4}{K_0}
e 2 = ∣ ∣ v 0 v 4 ∣ ∣ 2 = K 0 K 4
と表されることに注意します。
II(1)の解答より
K 4 = 3 2 R ( T 3 − T 4 )
K_4 = \dfrac{3}{2} R (T_3 - T_4)
K 4 = 2 3 R ( T 3 − T 4 )
両辺を K 0 = 1 2 m v 0 2 K_0 = \dfrac{1}{2} m v_0^2 K 0 = 2 1 m v 0 2
K 4 K 0 = e 2 = 3 2 R ( T 4 − T 3 ) K 0
\dfrac{K_4}{K_0} = e^2 = \dfrac{\dfrac{3}{2} R (T_4 - T_3)}{K_0}
K 0 K 4 = e 2 = K 0 2 3 R ( T 4 − T 3 )
右辺について,分子・分母それぞれを U 0 = 3 2 R T 0 U_0 = \dfrac{3}{2} R T_0 U 0 = 2 3 R T 0
e 2 = T 3 T 0 − T 4 T 0 K 0 U 0 = U 0 K 0 ( T 3 T 0 − T 4 T 0 )
e^2 = \dfrac{\dfrac{T_3}{T_0} - \dfrac{T_4}{T_0}}{\dfrac{K_0}{U_0}} = \dfrac{U_0}{K_0} \left( \dfrac{T_3}{T_0} - \dfrac{T_4}{T_0} \right)
e 2 = U 0 K 0 T 0 T 3 − T 0 T 4 = K 0 U 0 ( T 0 T 3 − T 0 T 4 )
(2-1)式から(2-3)式の結果を使って,温度の比は V 0 / V 1 V_0/V_1 V 0 / V 1
( V 0 V 1 ) 2 3 = α > 1
\left( \dfrac{V_0}{V_1} \right)^{\frac{2}{3}} = \alpha > 1
( V 1 V 0 ) 3 2 = α > 1
とおきます。
まず(2-1)式より
T 1 = α T 0
T_1 = \alpha T_0
T 1 = α T 0
次に(2-2)式より
∴ T 3 = T 0 + T 1 2 = 1 + α 2 T 0
\therefore T_3 = \dfrac{T_0 + T_1}{2} = \dfrac{1 + \alpha}{2} T_0
∴ T 3 = 2 T 0 + T 1 = 2 1 + α T 0
最後に(2-3)式より
T 4 = T 3 T 1 T 0 = 1 α 1 + α 2 T 0 = 1 2 ( 1 + 1 α ) T 0
T_4 = \dfrac{T_3}{T_1} T_0 = \dfrac{1}{\alpha} \dfrac{1 + \alpha}{2} T_0 = \dfrac{1}{2} \left( 1 + \dfrac{1}{\alpha} \right) T_0
T 4 = T 1 T 3 T 0 = α 1 2 1 + α T 0 = 2 1 ( 1 + α 1 ) T 0
これらより
e 2 = U 0 K 0 ( T 3 T 0 − T 4 T 0 ) = U 0 2 K 0 ( α − 1 α )
e^2 = \dfrac{U_0}{K_0} \left( \dfrac{T_3}{T_0} - \dfrac{T_4}{T_0} \right) = \dfrac{U_0}{2 K_0} \left( \alpha - \dfrac{1}{\alpha} \right)
e 2 = K 0 U 0 ( T 0 T 3 − T 0 T 4 ) = 2 K 0 U 0 ( α − α 1 )
α \alpha α K 0 K_0 K 0 U 0 U_0 U 0 t = T 0 t = T_0 t = T 0 t = t 1 t = t_1 t = t 1
K 0 + U 0 = 0 + 3 2 R T 1
K_0 + U_0 = 0 + \dfrac{3}{2} R T_1
K 0 + U 0 = 0 + 2 3 R T 1
辺々 U 0 = 3 2 R T 0 U_0 = \dfrac{3}{2} R T_0 U 0 = 2 3 R T 0
K 0 U 0 + 1 = T 1 T 0 = α
\dfrac{K_0}{U_0} + 1 = \dfrac{T_1}{T_0} = \alpha
U 0 K 0 + 1 = T 0 T 1 = α
これより
α − 1 α = α 2 − 1 α = ( K 0 U 0 ) 2 + 2 K 0 U 0 K 0 U 0 + 1
\begin{aligned}
\alpha - \dfrac{1}{\alpha} &= \dfrac{\alpha^2 - 1}{\alpha} \\
&= \dfrac{(\dfrac{K_0}{U_0})^2 + 2 \dfrac{K_0}{U_0}}{\dfrac{K_0}{U_0} + 1}
\end{aligned}
α − α 1 = α α 2 − 1 = U 0 K 0 + 1 ( U 0 K 0 ) 2 + 2 U 0 K 0
これより
e 2 = U 0 2 K 0 ( K 0 U 0 ) 2 + 2 K 0 U 0 K 0 U 0 + 1 = 1 2 K 0 U 0 + 2 K 0 U 0 + 1 = 1 2 K 0 + 2 U 0 K 0 + U 0
\begin{aligned}
e^2 &= \dfrac{U_0}{2 K_0} \dfrac{(\dfrac{K_0}{U_0})^2 + 2 \dfrac{K_0}{U_0}}{\dfrac{K_0}{U_0} + 1} \\
&= \dfrac{1}{2} \dfrac{\dfrac{K_0}{U_0} + 2}{\dfrac{K_0}{U_0} + 1} \\
&= \dfrac{1}{2} \dfrac{K_0 + 2 U_0}{K_0 + U_0}
\end{aligned}
e 2 = 2 K 0 U 0 U 0 K 0 + 1 ( U 0 K 0 ) 2 + 2 U 0 K 0 = 2 1 U 0 K 0 + 1 U 0 K 0 + 2 = 2 1 K 0 + U 0 K 0 + 2 U 0
e e e
e = 1 2 K 0 + 2 U 0 K 0 + U 0
e = \sqrt{\dfrac{1}{2} \dfrac{K_0 + 2 U_0}{K_0 + U_0}}
e = 2 1 K 0 + U 0 K 0 + 2 U 0
となります。
エネルギー保存則とポアソンの公式をうまく用いる問題です。