力学的エネルギー保存則の導出と例題
この記事では,力学的エネルギー保存則を解説します。エネルギー保存則は,物理学で最も重要な法則と言っても過言ではありません。
この記事に関連するQ&A
エネルギーとは
エネルギーとは
物理学で(あるいは日常生活全般で)よく耳にする用語としてエネルギーがあります。エネルギーとは,いわば地球上の水のようなものです。水は,海にあったり,氷として南極にあったり,雲になり雨として降ってきたり,人間に飲まれたりしますが,地球上にある水の総量は変わりません。これと同じように,エネルギーもいろいろな形に姿を変えますが,全宇宙ではその総量は変化しないと考えられています。このことをエネルギーの保存という言葉で表現します。(水の例は筆者が考えたので伝わりづらいかもしれませんが,要は全エネルギーの不変性が,エネルギーという概念の一番重要な特徴だということです。)
例えば,エネルギーの形としては,代表的なものだけでも以下のようにたくさんあります。
- 熱エネルギー
- 運動エネルギー
- 位置エネルギー
- 電磁エネルギー
- …
ここで運動エネルギーが熱エネルギーへと形を変えることがありますが,全エネルギーは一定です。
ここまで繰り返し強調した,「全エネルギーは保存する」という事実には,どのような根拠があるのでしょうか。これからそのことについて,エネルギーの中でも特に力学的エネルギーに焦点を絞って解説していきます。
運動方程式と力学的エネルギー保存則
運動方程式と力学的エネルギー保存則
結論から言うと,全エネルギー保存則は基本方程式を根拠にしています。つまり,力学的エネルギーの場合,その保存則は運動方程式から導出されるものだということです。では,実際に導出してみましょう。
運動方程式は です。
運動方程式の両辺について, と内積をとると, となります。ここで, を利用しています。ここで
について両辺をについて積分することを考えます。左辺は明らかに となります。この項を運動エネルギーと言います。
を用いると,右辺は
となります。この項は,物体を曲線 にそって動かした時,系に与える仕事を表しています。力学的エネルギーが保存するのは,この仕事が の取り方によらないことです。すなわち,経路の始点と終点の座標 のみの関数を用いて仕事が と表されることが条件になります。のことを,位置エネルギー,もしくはポテンシャル関数と呼びます。また,仕事が経路によらない時, を保存力と言います。 は一定なので,積分定数とまとめて定数とおけます。よって,以上より
がわかりました。
導出で仕事という用語を使いましたが,仕事とエネルギーは表裏一体の概念です。仕事とエネルギーの関係については以下の記事で解説してあります。
仕事と運動エネルギーの関係
力学的エネルギー保存の法則の利用
力学的エネルギー保存の法則の利用
ここまでで運動方程式は,古典力学において導出できない原理であるのに対して,力学的エネルギー保存則はそこから導出される公式だということを解説しました。ではなぜわざわざ力学的エネルギー保存則を考えるのでしょうか。
その1つの理由として,運動方程式を用いると,質点の位置を時間の関数として求めることができますが,いつでも求めることができるとは限りません。そういう場合でも,エネルギー保存を使えば,「粒子がこの位置にいるとき,粒子はこの速度をもつ」という部分的な情報ならばを得ることができることがあります。
例として以下の問題に取り組んでみましょう。
質量 の質点を,滑らかな地面に置かれた台車の斜面の一番上(最下点からの高さ )から,図のように転がした。質点は斜面から一度も離れることなく斜面の最下点の壁に衝突した。
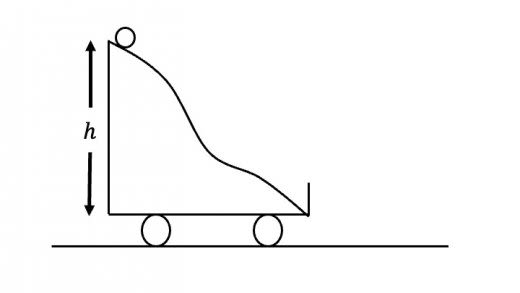 (1)台車が地面に固定されているとき,壁に衝突する直前の質点の速さを求めよ。
(1)台車が地面に固定されているとき,壁に衝突する直前の質点の速さを求めよ。
(2)質点が壁に激突した直後,質点は壁にくっついて壁に対して静止した。この時,台車の速さ を求めよ。ただし図中右向きを正とすること。

解答の方針は以下のようになります。
(1)運動方程式を立てたいのですが,斜面の曲線形がわからない上に,万が一分かったとしても斜面から質点にはたらく垂直抗力は時々刻々変わるので容易ではありません。ここで活躍するのが力学的エネルギー保存の法則です。すなわち,求める速さを とすると 左辺は始状態での位置エネルギー,右辺は終状態での運動エネルギーです。これを解いて, がわかります。
(2)系全体に対して運動量保存則を使うと, となり, がわかります。
力学的エネルギー保存則とHamilton力学
実は運動方程式ではなく,力学的エネルギー保存則を主役にした理論を構築することができます。この理論は,創始した物理学者の名前にちなみ,Hamilton力学と呼ばれています。実は,運動方程式を主役にしたNewton力学と力学的エネルギー保存則を主役にしたHamilton力学は,物理的には同値なのですが,量子力学との接続という観点から見ると後者の方が都合がいい場合があります。これが力学的エネルギー保存則を考える2つ目の理由です。
エネルギー保存を破る現象は,いまだに1つも見つかっていません。











