【解答・解説】東大物理2025 第1問 -力学-
本記事中の図は全て,2025年度東京大学入試問題物理第1問を参考に,ライターが作成したものです。
図1-1のように,3個のおもりと3本の棒を互いに固定した物体の運動を考える。
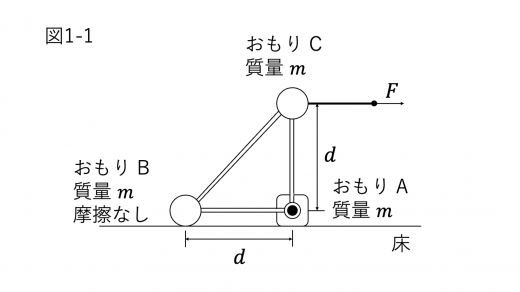
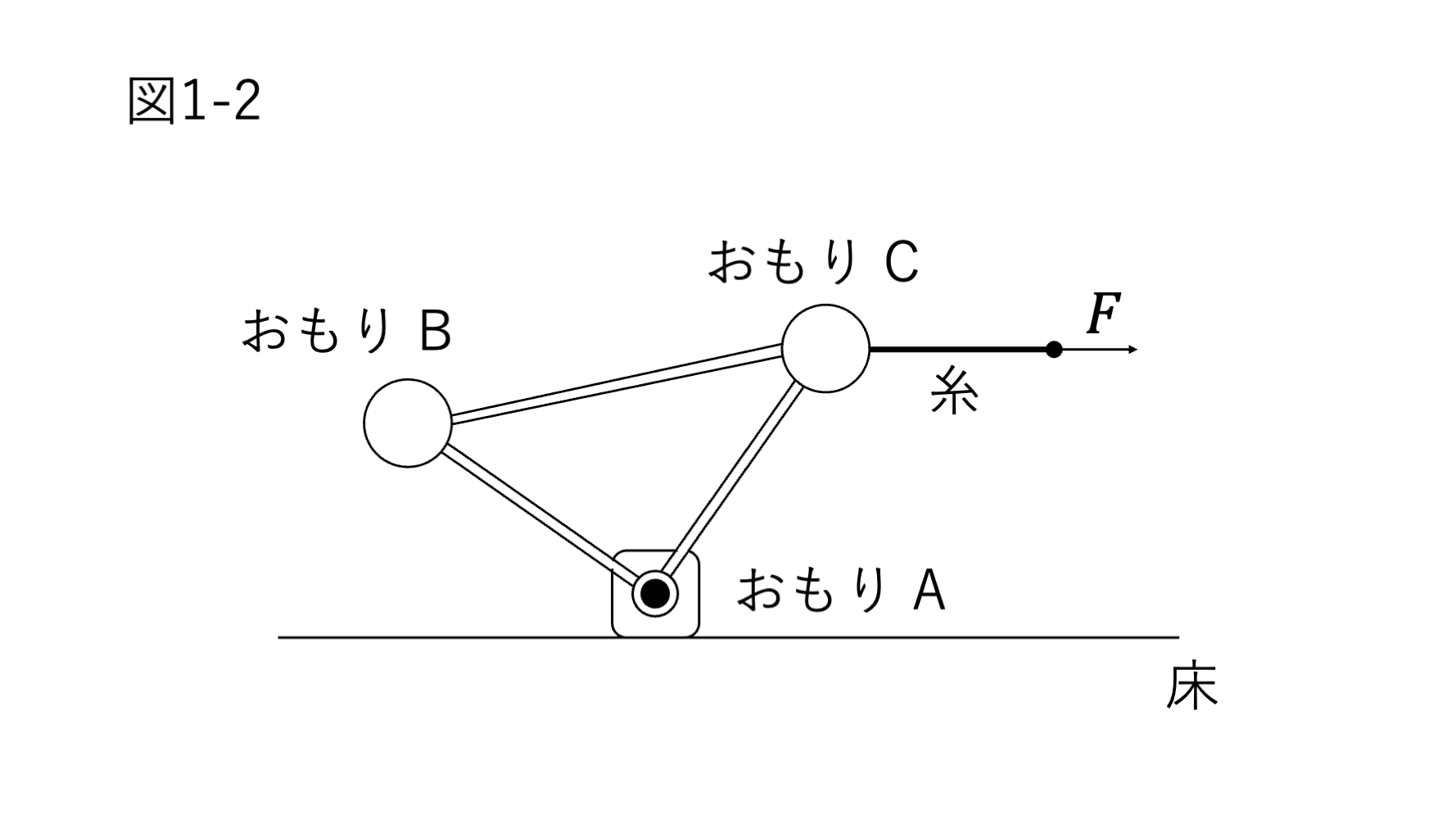
ただし,図1-2のように,おもり A に対して2本の棒はなめらかに回転できる。
はじめ物体は,図1-1のように,おもり A とおもり B が水平な床に接するように置かれており,おもり C はおもり A の真上にある。おもり C には水平に張られた糸がつながれており,糸を図の右方向に引く力の大きさを とする。3個のおもりの質量はいずれも であり,棒と糸の質量は考えなくてよい。おもり A からおもり C までの距離はいずれも であり,おもりの大きさは考えなくてよい。また,重力加速度の大きさを とする。
I まず,おもり A が床に固定されている場合を考える。
(1)図1-1の状態において, を徐々に大きくしていったところ, がある大きさに達したときにおもり B が床から離れた。このときの を求めよ。
(2)糸を引き続けて,図1-2のように物体を傾けていくことを考える。おもり B が床から離れてから糸を引く力がした仕事の大きさを とする。 がある大きさ を超えると,物体は倒れて,おもり C は床に衝突する。 を求めよ。
II 次に,おもり A が床に固定されていない場合を考える。図1-1のようにおもり A とおもり B は床に接している。おもり A と床との間の静止摩擦係数は であり,おもり B と床の間には摩擦はない。
(1) が小さく,物体が静止しているとき,おもり B が床から受ける垂直抗力の大きさを, を含む式で表せ。
(2)前問 II(1) のとき,おもり A が床から受ける垂直抗力の大きさを, を含む式で表せ。
(3) を徐々に大きくしていったところ, がある大きさに達したとき,おもり B が床に接したまま物体が右に動き始めた。このときの を求めよ。
III 最後に,おもり A とおもり B が床に接したまま,物体が右に傾いている場合を考える。おもり A と床との間の動摩擦係数は であり,おもり B と床との間には摩擦はない。
(1)図1-3のように,物体が等速直線運動をしているときの を求めよ。
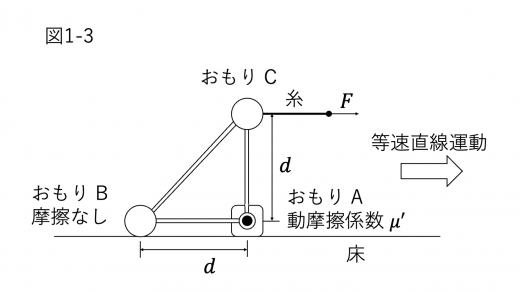
(2)糸を引くのをやめて にすると,物体は等加速度で運動する。このとき,図1-4に示すように,加速度は速度と逆向きであり,その大きさを とする。おもり B が床から受ける垂直抗力の大きさを, を含む式で表せ。
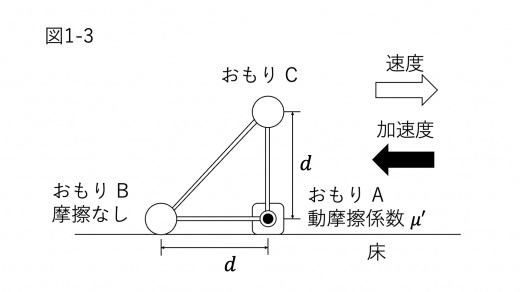
(3)前問 III(2) の を求めよ。
東大物理第1問を解説します。力学の基本的事項が問われる良問となっています。
解答例
解答例
愚直な解答例(力のつりあい)
この問題は全て,基本的に各物体の力のつりあい (力のつりあい・作用反作用との違い) や運動方程式 (運動方程式〜ニュートンの第2法則〜) を考えることで解くことができます。ここで紹介する愚直な解法では時間内に解き切るのは難しいかもしれないですが,この解法でも解けるということは理解しておいてほしいです。
I(1)
各物体の力のつりあいを考えます。ここで,Aは(明記されていない人工的な力によって)固定されていることから,BとCの力のつりあいを考えます。
まず C について,力のつりあいを考えます。
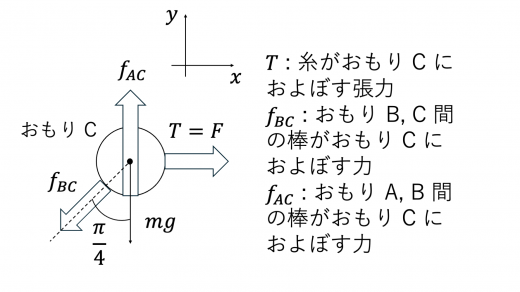
Cは図の 軸正の方向に張力 (張力の性質と種々の例題) を受けているので, 軸方向での力のつりあいのために,BC間の棒がCに加える力は上図のような向きになります。Cが糸から受ける力は,糸に対する力のつりあいと作用・反作用の法則により, となることに注意します。 軸方向の力のつりあいより
次に,B について力のつりあいを考えましょう。
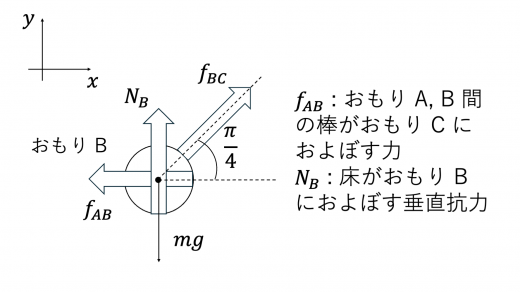
BC間の棒がBに加える力の向きは,BC間の棒の力のつりあいと作用・反作用の法則より,上図のようになります。 軸方向の力のつりあいより
おもり B が床から離れるとき,おもり B が床から受ける垂直抗力 が0となります。したがってこのときの は
I(2)
おもり B が床を離れてからさらに物体を傾けていくとどのように動くか,考えてみましょう。
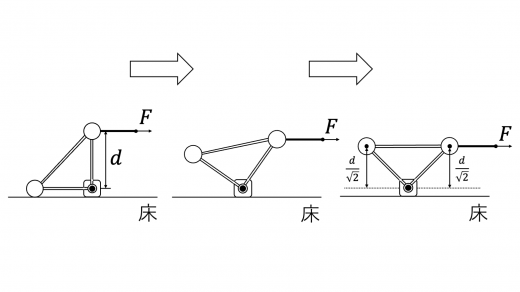
上図のように物体は傾いていき,やがて上最右図のようにおもり B と C の高さが一致します。そして,さらに糸を引いておもり B の高さが C のそれを上回るとき,物体が倒れると考えられます。
したがって, は,おもり B と C の高さが一致しているときの系全体の位置エネルギー (位置エネルギーの定義と例(重力・弾性力・クーロン力)) から,おもり B が床を離れ始めるときの系全体の位置エネルギーを引くことで求められます。各おもりの質量は全て なので
と求められます。
II(1)
I同様に,各物体の力のつりあいを考えます。
まず C について考えます。

力のつりあいより
(2-2)より
次に,B について考えます。
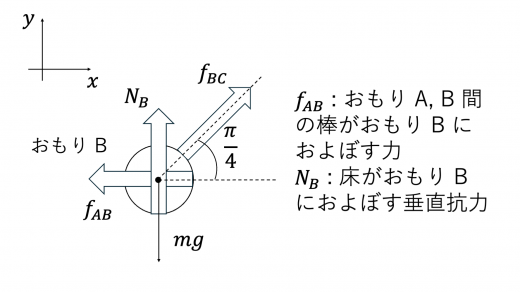
力のつりあいより
(2-4)より
と求められます。
II(2)
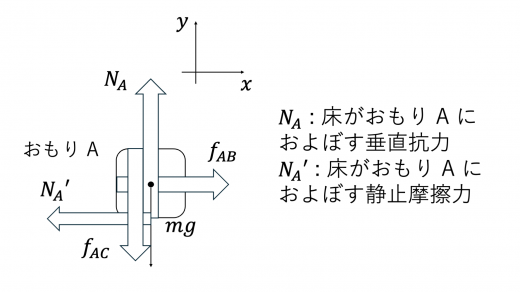
さらに A についても力のつりあいを考えます。
静止摩擦力については: 摩擦力の定義|動摩擦力・静止摩擦力・摩擦係数の解説
の向きはおもり A,B 間の棒の力のつりあいおよび作用・反作用の法則より, 軸正の向きにはたらきます。したがって,床がおもり A におよぼす力は図のように 軸負の向きにはたらきます。よって,力のつりあいより
(2-2)より
したがって,(2-6)より
となります。
II(3)
おもり B が床に接したまま物体が右に動き始めるとき,おもり A にはたらく静止摩擦力 が最大値 となります。
(2-3),(2-5)より となるので
より が保証されているので, で割る計算は許されます。
III(1)
系が等速直線運動で動いているとき,系全体および各物体の加速度は0であり,系全体および各物体で力のつりあいが成り立っています。さらに,おもり A と床との間には動摩擦力 がはたらいています。 および の表式はII(3)の場合と変わらないので,このときの はII(3)の解で とすればよく
と求められます。
III(2)
系および各物体は加速度 で減速運動します。系および各物体は 軸正の向きに運動しているので,おもり A には 軸負の向きに動摩擦力がはたらいていることに注意してください。
ここで,系と同じ加速度 で動く慣性系 (慣性系と非慣性系の定義|相対性原理と物理法則) を考えます。このとき各物体は力のつりあいが成り立っています。
まず,C について考えてみます。
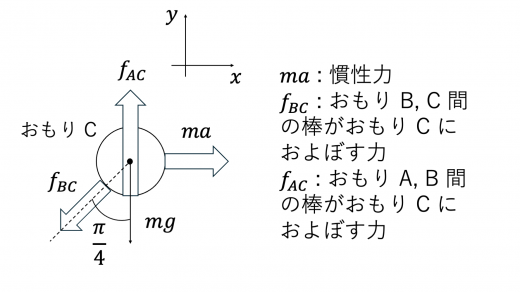
軸方向で力のつりあいが成り立つことより, は上図の方向にはたらきます。Cについて力のつりあいを考えて
次に B について考えてみます。
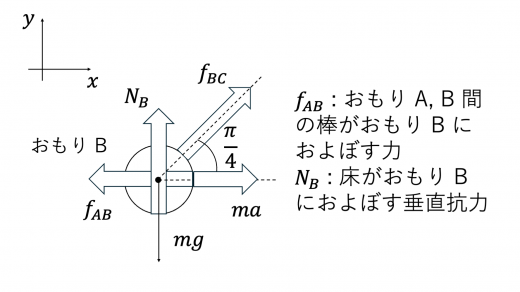
力のつりあいおよび作用・反作用の法則より, の向きが決まります。そして,B について,慣性力まで含めた力のつりあいが成り立つことより, の方向が 軸負の向きに決まります。B について力のつりあいを考えて
さらに A についても力のつりあいを考えます。
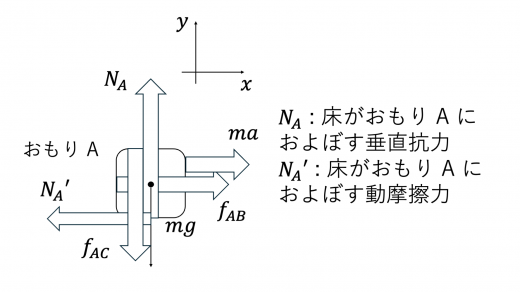
いま,A 含め系が図の 軸正の向きに運動していることより,A には 軸負の向きに動摩擦力がはたらくことに注意してください。
(3-1)より
よって,(3-4)より
と求まります。
(注)おもり B が床に接したままであることより, が要請されます。これより, が要請されます。
III(3)
(3-1)から(3-6)を連立方程式と考えます。未知数は の6つであり,方程式の数も6つなので,過不足なく全ての未知数を求められることがわかります。
前問の結果 も利用して,残りの未知数を求めていきましょう。
まず,(3-2)より
(3-3)より
(3-5)より
(3-6)より
これらより を消去して
(検算) より,まず がわかります。さらに より
したがって, が満たされていることもわかります。
よりスマートな解答例
全物体を1つの系とみなすことにより,いくつかの問題は楽に解くことができます。こちらも基本的な発想から思いつくことができます。この場合,剛体についての静止(あるいは回転運動)を考えることになるので,力のモーメント (力のモーメントと角運動量の関係) について考える必要が出てきます。
問題のいくつかについて,解答例を記載します。
I(1)
おもり,おもり間の棒および糸を合わせた系を考えます。このとき,系は大きさが無視できないので,剛体としての扱いが必要になります。
剛体が静止しているとき,(i)力のつりあいおよび(ii)力のモーメントのつりあいの両方が成り立っています。おもり A が床に固定されている状態でおもり B が床から離れるとき,この系がちょうど回転運動を始めるので,この直前まで力のモーメントのつりあいが成り立っていることになります。
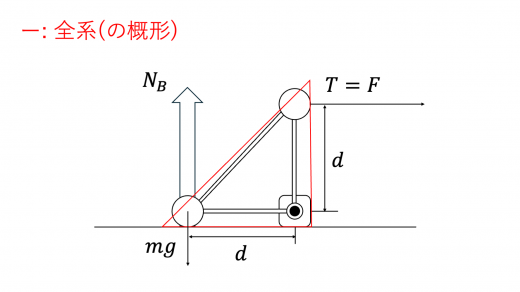
力のモーメントの始点を A(の重心) に定めると,このまわりの力のモーメントに寄与するのは,糸がおもり C を引く張力と,おもり B に加わる重力・垂直抗力の3つです。おもり B が床を離れるときには垂直抗力 が0となっているので,力のモーメントのつりあいより
と求められます。
II(1)
これも,おもり A を始点としたときの全系の力のモーメントのつりあいを考えます。この力のモーメントに寄与するのはおもり C にはたらく張力とおもり B にはたらく重力・垂直抗力です。したがって
II(2), (3)
全系にはたらく力のつりあいを考えます。
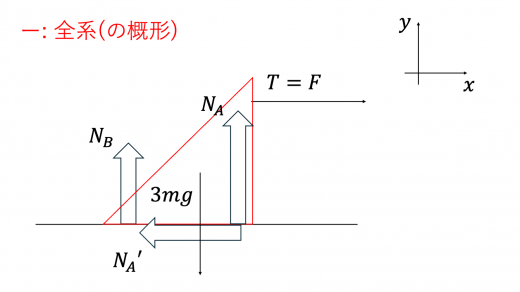
図の 軸方向について力のつりあいを考えて
さらに上図の 軸方向についても力のつりあいを考えて
物体が右に動き始める瞬間,静止摩擦力は最大値 になります。したがって
と求められます。
III(2), (3)
全系の慣性系を考えます。このとき,全系には慣性力まで含めた力のモーメントのつりあいおよび力のつりあいが成り立ちます。
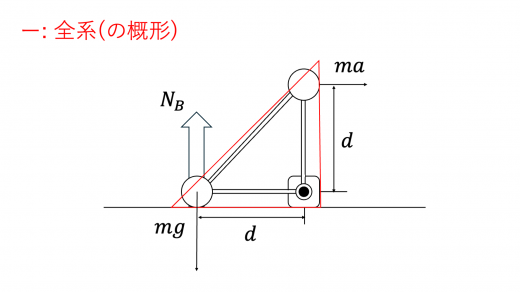
おもり A まわりでの力のモーメントのつりあいより
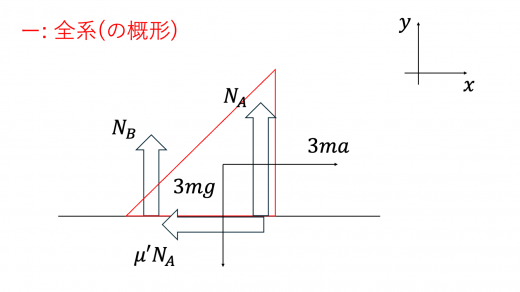
さらに,上図の 軸方向で力のつりあいより
これらを について解いて
力学の基本的な概念である,力のつりあいや力のモーメント,作用・反作用の法則などの理解を問うてくる,非常に良い問題だと感じます。何度も解き直す価値のある1問ではないでしょうか。











