【解答・解説】京大物理2025 第3問 -熱力学-
2025年度の京大物理第3問を解説します。熱力学の単元です。
この記事に関連するQ&A
問題
問題
以下の問題は,2025年度京都大学入試問題物理第3問から引用しています(一部修正しています)。
なお,本記事中の図は全て,2025年度京都大学入試問題物理第3問を参考に,ライターが作成したものです(一部見やすさ等のためライターが変更した部分があります)。
次の文章を読んで, に適した式または数値を,{ } からは適切なものを一つ選びその番号を,それぞれの解答欄に記入せよ。なお, はすでに で与えられたものと同じものを表す。また,問1,問2では,指示にしたがって,解答をそれぞれの解答欄に記入せよ。
(1) 1モルの単原子理想気体の状態変化について考える。絶対温度 におけるこの気体の内部エネルギーは, を気体定数とすると である。また,ゆっくりとした断熱変化では,この気体の圧力 と体積 の間にはポアソンの式 が成り立つ。以下,重力加速度の大きさを とする。
図1(a)に示すように,この理想気体を断面積が の円筒状の容器に入れ,蓋で封じる。
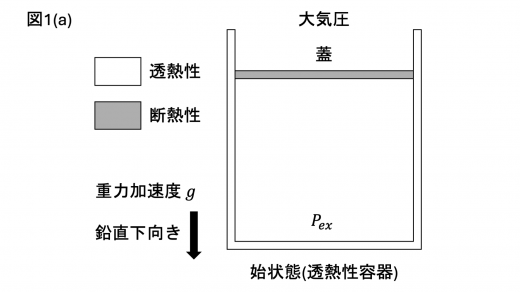
蓋は断熱性であり,気密性を失わずに鉛直方向に滑らかに動くことができる。容器は透熱性と断熱性に切り替えることができ,はじめ透熱性である。また,容器は十分に深く蓋が外れることはない。蓋にかかる重力による圧力と大気圧とを合わせた圧力を とする。 と理想気体の圧力が釣り合い,蓋は静止している。容器は透熱性のため外部と熱とのやり取りが十分速く行われ,理想気体の温度は周囲の大気と同じである。この状態を始状態と呼ぶ。
始状態において蓋に質量 のおもり O を静かに載せ,ゆっくりと気体を圧縮すると,気体の圧力と体積がそれぞれ で蓋は静止した。この状態を状態 X とする (図1(b))。 である。
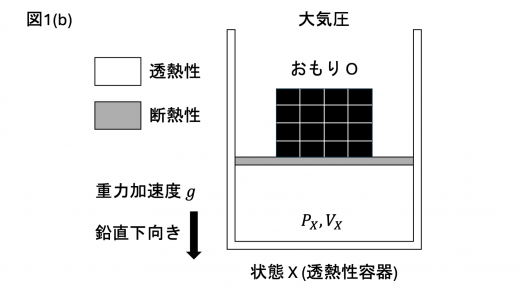
次に,状態 X における容器を断熱性に切り替え,外界との熱の出入りができないようにした (図1©)。
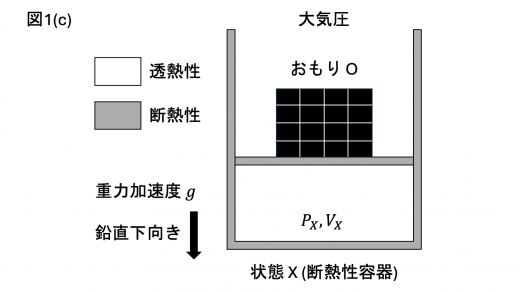
また,おもり O は 個の等価な小さなおもり c からなり,おもり c を1個ずつ取り除くことで気体にかかる圧力を変えることができる。ここで, は十分大きな正の整数で,おもり c を1個取り除くことによる外部から気体にかかる圧力の変化量は小さく,また気体の膨張による体積の変化量も小さい。以下の操作 を繰り返し,おもり c を1個ずつ取り除いていく。
- 操作 :おもり c を1個素早く取り除き,蓋が静止するまで膨張させる。
操作 を 回繰り返した後の理想気体の圧力と体積をそれぞれ とする。ここで, は 〜 の整数であり, は状態 X に対応している。 を用いると である。操作 を 回行った後にさらに操作 を1回行う。このとき気体がする仕事は, が十分大きいので, と近似できる。また,内部エネルギー変化は, を用いると, と表される。これらを用いることで, の関係式を得る。操作ごとの圧力変化と体積変化をそれぞれ とおくと
の関係式が得られる。 が大きくなると と は 0 に近づくので,操作 の繰り返しは,気体の圧力と体積が連続的に変化するものとみなすことができ,ポアソンの式が得られる。
状態 X から操作 を 回繰り返すと,全てのおもり c が取り除かれる。図1©の状態から開始して,断熱的におもり c を 個取り除いた場合の最終的な気体の圧力と体積を とする。一方,図1(b)の場合から開始して,等温的におもり c を 個取り除いた場合の最終的な気体の圧力と体積は であるとする。 と を比較すると {か:① ,② ,③ } である。
問1 {か} の大小関係について,理想気体の膨張による仕事と内部エネルギー変化をもとに説明せよ。
(2) 単原子分子理想気体とは異なる状態方程式や内部エネルギーの式に従う気体 F の状態変化について考える。ただし,この気体 F は考えている温度や圧力の範囲で気体として振る舞う。また,熱力学第一法則に従い,理想気体と同様に加熱すると圧力が上昇し,気体がする仕事は理想気体と同様に表される。この気体の圧力,体積,内部エネルギーをそれぞれ とすると,気体 F について であることがわかっている。
気体 F の断熱膨張を考える。気体の体積が から に微小変化するとき,圧力は から に,内部エネルギーは から に,それぞれ微小変化するとする。ここで, である。また,以下では などの微小量どうしの積は無視してよい。この微小変化により気体がする仕事を, から必要なものを用いて表すと となる。したがって
が得られる。これより,気体 F のゆっくりとした断熱変化において ) の関係が成り立つことが示される。
単位体積あたりの内部エネルギーはエネルギー密度と呼ばれる。気体 F のエネルギー密度を とすると である。気体 F のエネルギー密度は,絶対温度 のみに依存し と表されることがわかっている。ここで, と は正の定数である。気体 F を作業物質とするサイクルを考えることで を求めてみよう。このサイクルでは,図2に示すように,気体は状態 A → 状態 B → 状態 C → 状態 D → 状態 A のように変化し,もとに戻る。
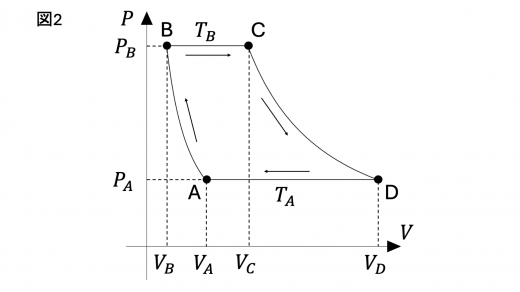
各変化は,
- 状態 A → 状態 B:気体を断熱壁で覆った断熱変化
- 状態 B → 状態 C:絶対温度 の熱源に気体を接触させた等温変化
- 状態 C → 状態 D:気体を断熱壁で覆った断熱変化
- 状態 D → 状態 A:絶対温度 の熱源に気体を接触させた等温変化
である。ここで,各変化はゆっくりと進行し,また各状態での気体の体積と圧力は図2に示す通りである。以下では,状態 i から状態 j への変化で気体が得た熱を と表す。ここで,i と j は A ~ D のいずれかを指す。
状態 B の体積 は, と を用いると となる。気体 F の は だけでなく にも依存することに注意すると, は, を用いて と表される。また, を を用いて表すと となる。
ゆっくりと進む等温変化と断熱変化からなるサイクルについて,一般に次の事実が知られている。高温 (絶対温度 ) の熱源から得た熱を ,低温 (絶対温度 ) の熱源から得た熱を とすると, の関係が成り立つ。これを気体 F のサイクルにあてはめると
が得られる (ただし, と は を用いて表せ)。この式が任意の と について成り立つことから となる。
問2 気体 F の定圧モル比熱は定義することができない。その理由を述べよ。
大きく二つのパートに分かれます。前半は通常の断熱変化の公式 (断熱変化におけるポアソンの式の導出) を導出する問題です。後半は,通常とは異なる状態方程式にしたがう気体の振る舞いについて考察する問題です。
解答例
解答例
(1)
まず,図1(a) から 図1(b) (状態 X) への気体の状態変化を追います。
大気圧を ,蓋の質量を とします。図1(b) に関して,蓋に関する力のつりあいより
問題文より であるから,
次に,図1© のように容器を断熱性のものに替えてから,操作 を行っていきます。操作 を 回行った後の気体の状態について考えてみます。このときの気体の圧力・体積を とします。
このときの圧力 は
と書けます。
このあと,さらに操作 をもう一度行います (この状態変化を と呼びます)。このとき気体の圧力・体積を とします。
この操作で気体がした仕事 を考えます。 が十分大きいとき,圧力の変化は非常に小さいと考えることができます。したがって,問題文に与えられているように,
と書くことができます。
また,操作 を 回行った後の気体の温度をそれぞれ とすると,理想気体の状態方程式 (ボイル・シャルルの法則と状態方程式) より
したがって, における内部エネルギーの変化 は
は断熱変化なので,この状態変化により気体が受け取った熱量は です。したがって,熱力学第一法則 (熱力学第一法則|仕事と内部エネルギーの関係) より
代入して整理すると
と表されます (え:)。
もう一段階変形すると
となります。
を用いて, を消去します。問題文の形から, が現れるように変形します。
まず を消去します。
次に を消去します。
問題文に合うように整理して
となります (お:)。
を十分大きくすると は 0 に近づくので,操作 の繰り返しは,気体の圧力と体積が連続的に変化するとみなすことができ,ポアソンの公式が得られます。
(補足) 気体の圧力と体積が連続的に変化するとみなせることから,気体の圧力 および は
は十分小さく と書き直すことができます:
両辺を積分して
と,ポアソンの公式が得られます。
状態 X を 回繰り返し,全てのおもりを取り除く (この 状態変化を と呼びます) ことを考えます。
まず,図1© から を経た気体の状態を Y とし,圧力・体積をそれぞれ とします。 であり,ポアソンの公式より
一方,図1(b) から により等温変化した後の気体の状態を Z とし,圧力・体積を とします。 であり,ボイルの法則 (ボイル・シャルルの法則と状態方程式) より
これより, と を比較すると,か:① () であることがわかります。
問1
図1© から状態 Y への変化は断熱変化であるから,この間に気体が外部にした仕事および内部エネルギー変化をそれぞれ とすると
より は図1© の状態から下がります。
一方図1(b) から状態 Z への変化は等熱変化であり,図1(b)(および図1©) と状態 Z の温度は一定です。状態 Y と状態 Z の圧力は同じであることから,理想気体の状態方程式より, の方が より小さいことがわかります。
(2)
単原子分子理想気体とは異なる状態方程式や内部エネルギーの式に従う気体 F を考えます。F の圧力,体積がそれぞれ であるとき,F の内部エネルギー は であることがわかっています。
いま,気体 F が断熱変化により膨張し,気体と圧力がそれぞれ に微小変化したとします。 が微小量であることより,この変化中に気体がする仕事 は,F の圧力が常に であるとして求めることができ,
と求めることができます。
(補足) 仮に,変化中の F の圧力が常に だとしても,問題文より微小量の積は無視できることから と求められます。
また,この変化による内部エネルギーの変化 は,同様にして
と求められます。したがって,この変化が断熱変化であることより
(1)での議論と同様にして,断熱変化における F の圧力と体積の関係として
という関係が得られます。 (く) です。
ここで,F のエネルギー密度 は, と,温度 にのみ依存することがわかっているとします (これより, が にのみ依存し, であることもわかります)。問題文に与えられたサイクルにより を求めましょう。
まず,状態 A → 状態 B の変化を考えます。断熱変化であることから
となります (け:)。
状態 B → 状態 C の変化では圧力は で一定なので,熱力学第一法則より, は
と求められます。
同様に を求めると
となります。
より, であることがわかるので,問題文に与えられた式より
となります。
問題文の形に合わせるために,まずは を で表すことを考えます。 については,けより で表されています。同様に, についても考えます。状態 C → 状態 D の断熱変化より
これらより を消去して
問題文の形に合うように整理して
となります (し:,す:)。
この式が任意の について成り立つことから,しおよびすの各項が常に0となることがわかります。つまり
いずれの式も,A の物理量と B の物理量について整理すると
これより
したがって,せ: となります。
問2
上記の議論より,内部エネルギーは温度にのみ依存し,また F の圧力は温度にのみ依存することがわかっています。
一方,定圧モル比熱 (気体の状態変化とモル比熱(断熱変化,等温変化,定圧変化など)) は,圧力を一定として温度を変化させたとき,内部エネルギーを温度変化で割ることで得られていました。しかし,気体 F の場合は,圧力を一定とすると温度は一つに定まってしまい,変化させることができません。
したがって,気体 F の定圧モル比熱は定義できないということになります。
問2のような問題は,入試問題ではあまり見られないタイプの問題かもしれません。
問題文中のサイクル内の等圧変化のグラフがヒントになっています。











