【解答・解説】京大物理2025 第2問 -電磁気-
2025年度の京大物理第2問を解説します。電磁気の単元です。
この記事に関連するQ&A
問題
問題
以下の問題は,2025年度京都大学入試問題物理第2問から引用しています(一部修正しています)。
なお,本記事中の図は全て,2025年度京都大学入試問題物理第2問を参考に,ライターが作成したものです(一部見やすさ等のためライターが変更した部分があります)。
次の文章を読んで, に適した式または数値を,{ } からは適切なものを一つ選びその番号を,それぞれの解答欄に記入せよ。なお, はすでに で与えられたものと同じものを表す。また,問1〜問3では,指示にしたがって,解答をそれぞれの解答欄に記入せよ。ただし,円周率を とし,以下に登場する物質や気体の透磁率はすべて とする。
(1)図1のように,長さ ,半径 の円周に抵抗の無視できる導線を一様に 回巻き付けて作ったソレノイド(以下コイルとよぶ)がある。
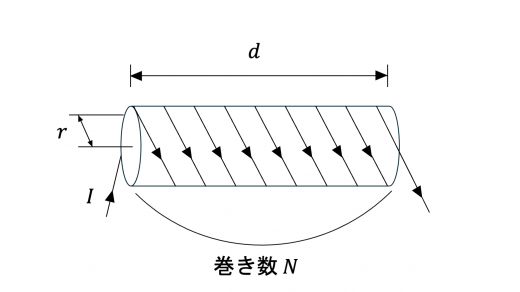
円筒内部は気体で満たされており,コイルの長さ は と比べて十分長く,このコイルに電流を流すと円筒内部には一様な磁束密度ができる。このコイルに外部電源を接続して電流 を流したときに円筒内部に発生する磁束密度の大きさは である。
次に,微小時間 の間に電流を から にゆっくりと変化させると,コイルには誘導起電力 が発生する ( は微小量であり,起電力の符号は電流の上流側の電位が高い場合を正とする)。このことから,このコイルの自己インダクタンスは である。また,時間 の間に外部電源がコイルにした仕事は である。
図1のコイルに電流 が流れているとき,コイルにはエネルギー が蓄えられている。コイルを流れている電流が から に変化する際のこのエネルギーの増加は, を満たす十分小さな に対して成立する近似式
を使うと となり,外部電源がコイルにした仕事と一致する。つまり,外部電源が行った仕事がコイルのエネルギーとして蓄積される。
(2)図2のように,バルーンアート用の風船のような細長い円筒形状をした伸縮自在の閉じた膜に,伸縮自在で抵抗の無視できる導線を巻き数密度 (円筒軸方向の単位長さ当たりの導線の本数) が一様となるように 回巻き付けて作ったソレノイド (以下コイルとよぶ) がある。
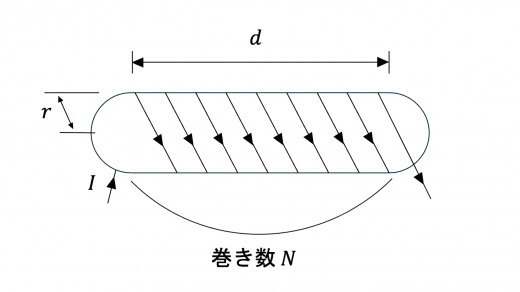
膜内部の気体の量は調節でき,このとき膜は円筒形状を保ったまま半径や長さが変わる。導線は膜に接着されており,膜の半径や長さが変化するとき導線は膜に接したままむらなく伸び縮みし,巻き数密度は一様に保たれるものとする。また,膜は厚みの無視できる絶縁体でできており,膜と導線は容易に伸縮するものとし,膜の面積,導線の長さおよび形状の変化に要する仕事は十分小さく無視できるものとする。
なお,以下では必要に応じて近似式 (1) を使って を無視し,解答欄には を使わずに解答を記入せよ。
まず,コイルの両端を固定装置で固定して動かないようにし,膜の長さが に保たれるようにした。この状態でコイルに電流 を流し,膜内部の気体の量を調節して,図2のようにコイルの半径が となる状態を作った。このとき,コイル内部には一様な磁束密度 が発生した。この状態から,電流 を一定に保ったまま膜内部の気体の量をゆっくり増加させたところ,コイルの半径は速さ で大きくなり,微小時間 ののちに になった。このとき,コイル一巻きを貫く磁束は の間に だけ増加するので,コイルには誘導起電力 が発生する (起電力の符号は電流の上流側の電位が高いときを正とする)。また,時間 の間に外部電源がコイルに対して行う仕事は である。
一方,コイルに蓄えられるエネルギー () は,コイル半径が大きくなったことにより時間 の間に だけ増加する。このエネルギーの変化は,外部電源が行った仕事 と,膜内外の気体の圧力差が膜に対して行った仕事の和に等しい。時間 の間にコイルの体積は だけ増加するので,膜内部の気体の圧力差を
とすると,膜内外の気体の圧力差が時間 の間に膜に対して行う仕事は を使って と書ける。以上のことから膜内外の気体の圧力差 を求めることができ, と で求めたコイル内部の磁束密度 のみを用いて表すと と書ける。
いま,膜には膜内外の気体がもたらす圧力差に加え,電流 が作り出す圧力が働いている。これらの圧力がつり合いの条件を満たすことから,電流 が作り出す圧力は,{ワ:①コイルを膨らませる方向に働いている,②コイルを収縮させる方向に働いている,③働いていない}。
(3)コイルを図2の状態に戻してから,コイルの半径を に固定したうえでコイルの円筒軸方向の長さを自由に変化させられるようにした。コイルの円筒軸方向の長さが の状態から,電流 を一定に保ったまま膜の内部の気体量を変化させたところ,円筒軸方向の長さが速さ でゆっくりと大きくなり,微小時間 ののちに になった。このとき, を満たす十分小さな に対して成り立つ近似式
を使って の2次以上の項を無視すると,微小時間 の間に外部電源がコイルに対して行う仕事は であることがわかる。このとき問1〜問3に答えよ。
問1 膜内外の圧力差を
とするとき, を求めよ。ただし,近似式 (ii) を使って の2次以上の項を無視し,解答には と で求めたコイル内部の磁束密度 のみを用いよ。
問2 電流 がコイルの両端面に作り出す圧力の向きについて,適切なものを以下から選んで番号を解答欄に記入せよ。
-
① コイルが円筒軸方向に伸びようとする圧力が働いている。
-
② コイルが円筒軸方向に縮もうとする圧力が働いている。
-
③ 圧力が働いていない。
問3 問2の結果を,コイルを形成する各一巻きの導線を流れる電流が相互におよぼす力に基づいて簡潔に説明せよ。
近似を用いながらソレノイドに働く誘導起電力について考察する問題です。
以下では問題文に倣い,ソレノイドのことをコイルと呼びます。
解答例
解答例
(1)
コイル中心にはたらく磁束密度は,公式 (電流と磁束密度の関係) より
と求められます。
微小時間 の間に電流が から にゆっくり変化したとき,磁束密度の変化を とすると
いま,円筒内部には一様な磁束密度が働いていることにより,微小時間 でのコイル内の磁束の変化 は
だけ変化します。
いま, が正の量とすると,コイル内の磁束は図1の水平右向きに変化するので,誘導起電力はコイル内の磁束を図1の水平左向きに増やす方向に働きます。右ねじの法則 (電流と磁束密度の関係) より,この起電力は電流を下流から上流に流す方向に働き,したがってこの誘導起電力は正となります。ファラデーの電磁誘導の法則 (電磁誘導とレンツの法則) より,誘導起電力は
と求められます (ロ:)。
一方,コイルに流れている電流が時間変化するとき,コイルにはたらく誘導起電力 は,自己インダクタンスを とすると (自己誘導と自己インダクタンス|回路に生じる逆起電力の導出),向きまで含めて
したがって,自己インダクタンス は
と表されます。
また,電流の変化がゆっくりであることから,微小時間 の間に外部電源がした仕事 は,電荷 を 電圧 だけ運ぶ仕事に等しく
と求められます (ニ:)。
また,エネルギー保存則から,外部電源が行った仕事がコイルのエネルギーの変化 となるとして を求めることができます。
自己インダクタンス に電流 が流れているとき,コイルが蓄えるエネルギー は (コイルのエネルギーとエネルギー密度の解説)
いま電流が から に変化したときのエネルギーの変化を とすると,近似式 (1) より
(ハ) より
となり,これはたしかに と一致しています。
(2)
膜は「円筒状」であることに注意します。
コイルの半径が微小時間 の間に から へとゆっくり大きくなったとします。
このとき,コイル内の磁束密度は変化しませんが,磁束密度が貫く面積 は変化します。この変化を とすると,近似式 (1) より
これより磁束の変化 は
となります (ヘ:)。
したがって,コイルにはたらく誘導起電力 は,向きを含めて
となります (ト:)。
設問 (1) と同様に,外部電源がコイルに対して行う仕事 は
と求められます (チ:)。
一方,このときコイルが蓄えるエネルギーの変化を とすると, より
と求められます (リ:)。
このエネルギー変化は,外部電源が行った仕事 と,膜内外の気体の圧力差が膜に対して行った仕事 の和に等しいとして,膜内外の気体の圧力差を求めます。
コイルの半径が のとき,コイルの体積 は
なので,半径変化に対するコイルの体積の変化 は
となります (ヌ:)。
いま, の定義より, は
と書けます (ル:)。
より
ここで, より なので
と書けます。
膜には膜内外の気体がもたらす圧力差に加え,電流 が作り出す圧力 が働いています。 より,膜外の気体の圧力のほうが膜内のそれより大きいので,膜に働く圧力のつりあいより, の方向はワ:① (コイルを膨らませる方向に働いている) となります。
(3)
今度は円筒の半径ではなく長さが変化します。外部電源がコイルに対して行う仕事を求めるために,誘導起電力を求めましょう。
まず,磁束の変化を考えます。コイル内の磁束密度 は
と表されていました。いま から へと変化するときの磁束密度の変化 は
磁束が貫く面積 はこの時間変化で不変なので,生じる誘導起電力は,向きまで含めて
外部電源が行う仕事 は,この誘導起電力に逆らって電荷を運ぶであり
と求められます (カ:)。
問1
(2)と同様にして,膜内外の気体の圧力差 を求めましょう。やはり,エネルギー保存則
を使います。
について考えます。コイルの自己インダクタンス の変化 は
したがって,コイルが蓄える内部エネルギーの変化 は
続いて膜内外の圧力差による仕事 について考えます。円筒の長さ変化に対する円筒の体積変化 は
したがって, は
より, は
と求められます。
問2
問1より, であることがわかります。(2)のヲ,ワでの議論と同様に考えて,電流 がコイルの両端面に作り出す圧力の向きは ② (コイルが円筒軸方向に縮もうとする向き) となります。
問3
コイルを形成する各一巻きの導線には,向きが同じ平行な電流が流れています。平行電流は互いに引き合う方向に力がはたらく (フレミングの左手の法則の復習・理論的解説|電磁力の定義|中学から高校まで) ために,問2では②の方向に電流による圧力が生じると考えられます。
近似を用いて2次以上の微小項を無視するのは,大学物理でも頻出の変形です。











