コイルのエネルギーとエネルギー密度の解説
この記事ではコイルのエネルギーについて解説します。コイルに密接に関係する概念として自己誘導と相互誘導があります。これに加え,コイルの逆起電力などの基本的な知識は以下の記事で解説してあるので,本記事を理解するための助けになると思います。
自己誘導と自己インダクタンス|回路に生じる逆起電力の導出
相互誘導と相互インダクタンスの定義|変圧器の回路の例題
この記事に関連するQ&A
コイルの磁気エネルギー(電磁エネルギー)の導出
コイルの磁気エネルギー(電磁エネルギー)の導出
エネルギーという概念は本来,系に変化を起こすために外部から行う仕事の逆符号として定義されるものです。この考え方をコイルにも適応して,コイルのエネルギーを求めてみましょう。
 上の図はコイルの模式図です。コイルに流れる電流が の状態から, になるまでに外部からする仕事を求めてみます。
上の図はコイルの模式図です。コイルに流れる電流が の状態から, になるまでに外部からする仕事を求めてみます。
微小時間 の間にコイルに流れる電流 を に外部から仕事を加えて変化させたとします。このとき,コイルに生じる逆起電力は でした。これに逆らって,電荷 を運ぶので,このとき外部から行う仕事は となります。 を と微分の形にして にわたって積分しましょう。 以上よりコイルに蓄えられるエネルギーを求めることができました。このエネルギーを一般に磁気エネルギー(電磁エネルギー)と言います。
回路方程式に現れる磁気エネルギー
回路方程式に現れる磁気エネルギー
上で得た結論を,回路の式を立てることで眺めてみましょう。
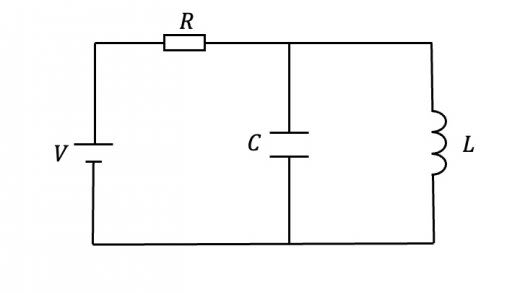 上のような回路があったとします。
上のような回路があったとします。
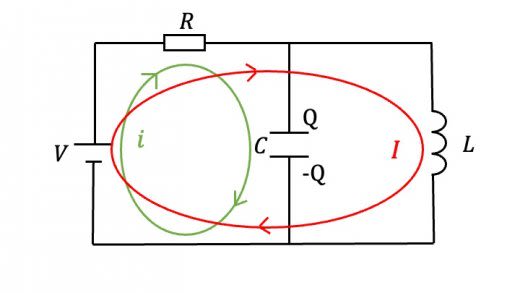 このように電流と電荷を設定して,キルヒホッフの法則に従って回路方程式を立ててみます。
また,関係式 が成り立ちます。この3式を用いて を計算し, を代入すると
となります。この式をよく観察してみると,左辺第1項は電池の仕事率,右辺第1項はコイルの単位時間あたりの磁気エネルギー,左辺第2項は抵抗で生じるジュール熱,左辺第3項はコンデンサーの単位時間あたりの静電エネルギーとなっていることがわかります! 以上より,上で求めた磁気エネルギーの表式を確認できました。
このように電流と電荷を設定して,キルヒホッフの法則に従って回路方程式を立ててみます。
また,関係式 が成り立ちます。この3式を用いて を計算し, を代入すると
となります。この式をよく観察してみると,左辺第1項は電池の仕事率,右辺第1項はコイルの単位時間あたりの磁気エネルギー,左辺第2項は抵抗で生じるジュール熱,左辺第3項はコンデンサーの単位時間あたりの静電エネルギーとなっていることがわかります! 以上より,上で求めた磁気エネルギーの表式を確認できました。
ソレノイドコイルと磁気エネルギー密度
ソレノイドコイルと磁気エネルギー密度
以下の例題を通して,磁気エネルギーにおいて重要な概念である,磁気エネルギー密度を学びましょう。
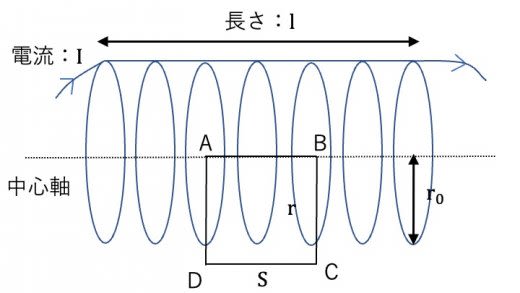 上に示すように,同線を半径 の円形上に一様に 回巻いたソレノイドコイルがある。真空の透磁率を として,以下の問いに答えよ。
上に示すように,同線を半径 の円形上に一様に 回巻いたソレノイドコイルがある。真空の透磁率を として,以下の問いに答えよ。
(1)図に示す長方形 にAmpereの法則を用いることで,ソレノイドコイルの中心軸上の磁場 を求めよ。
(2)ここで巻き数 のソレノイドコイルを貫く全磁束 は,ソレノイドコイルに流れる電流 と自己インダクタンス を用いて, とかける。 を を用いて表せ。
(3)コイルに蓄えられる磁気エネルギーを, のうち,必要なものを用いて表せ。
(1)
長方形 にAmpereの法則を適用してみましょう。長方形 を貫く電流は, なので,Ampereの法則より,
となります。よって
が得られます。
(2)
は磁場の強さであり,磁束密度 は, となります。よってソレノイドコイルを貫く全体の磁束 は,
となることがわかります。 に上の結果を代入して,
となります。
自己インダクタンスの定義は,磁束と電流を結ぶ比例係数であったので, と比較して,
が得られます。
(3)
(1)より,,(2)より, がわかっています。よって磁気エネルギーは
がわかります。ここで はソレノイドコイルの「体積」に相当する部分です。よってこの表式は
とみなすことができます。よって を磁場のエネルギー密度とよびます。
回路方程式を変形すると種々のエネルギーが勢揃いすることに,筆者は高校時代非常に感動しました。











