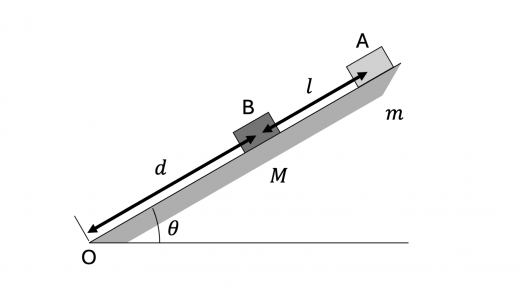
問1
(1)
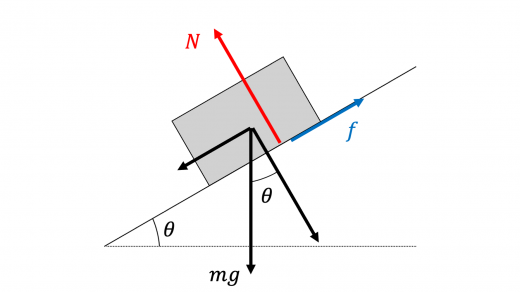
物体 A が静止しているときに,物体 A にはたらいている力を図示してみます。
物体 A が斜面から受ける垂直抗力 (摩擦力の定義|動摩擦力・静止摩擦力・摩擦係数の解説 ) の大きさを N A N_A N A 力のつりあい・作用反作用との違い )より
N A = m g cos θ
N_A = mg \cos{\theta}
N A = m g cos θ
と表すことができます。
(2)
静止摩擦力,動摩擦力の大きさをそれぞれ f A , f A ′ f_A, f_A' f A , f A ′
f A = m g sin θ
f_A = mg \sin{\theta}
f A = m g sin θ
と求められます。
(3)
物体 A が運動している場合は,動摩擦力と垂直抗力の関係より
f A ′ = μ 2 N A = μ 2 m g cos θ
\begin{aligned}
f_A' &= \dfrac{\mu}{2} N_A \\
&= \dfrac{\mu}{2} mg \cos{\theta}
\end{aligned}
f A ′ = 2 μ N A = 2 μ m g cos θ
と求められます。
問2
問2,問3では θ = π 6 \theta = \dfrac{\pi}{6} θ = 6 π
(4)
無視できるほど小さな力を加えて物体 A が斜面をすべり下り始めたことより,静止しているときには静止摩擦力が最大静止摩擦力と等しくなっていると考えられます。ゆえに,最大静止摩擦力の公式より
1 2 m g = μ 3 2 m g
\dfrac{1}{2} mg = \mu \dfrac{\sqrt{3}}{2} mg
2 1 m g = μ 2 3 m g
∴ μ = 1 3
\therefore \mu = \dfrac{1}{\sqrt{3}}
∴ μ = 3 1
と求められます。
(5)
斜面下側を運動の正の向きとします。A が運動しているときの斜面に水平な向きの加速度を a A a_A a A 運動方程式〜ニュートンの第2法則〜 ) より
m a A = 1 2 m g − μ 2 3 2 m g = 1 2 m g − 1 2 3 3 2 m g = 1 4 m g
\begin{aligned}
m a_A &= \dfrac{1}{2} mg - \dfrac{\mu}{2} \dfrac{\sqrt{3}}{2} mg \\
&= \dfrac{1}{2} mg - \dfrac{1}{2 \sqrt{3}} \dfrac{\sqrt{3}}{2} mg \\
&= \dfrac{1}{4} mg
\end{aligned}
m a A = 2 1 m g − 2 μ 2 3 m g = 2 1 m g − 2 3 1 2 3 m g = 4 1 m g
∴ a A = 1 4 g
\therefore a_A = \dfrac{1}{4} g
∴ a A = 4 1 g
よって,初めの位置を座標の原点とすると,時刻 t t t v A ( t ) v_A (t) v A ( t ) x A ( t ) x_A (t) x A ( t ) 等加速度運動・等加速度直線運動の公式 ) の公式より
v A ( t ) = a A t = 1 4 g t
v_A (t) = a_A t = \dfrac{1}{4} g t
v A ( t ) = a A t = 4 1 g t
x A ( t ) = 1 2 a A t 2 = 1 8 g t 2
x_A (t) = \dfrac{1}{2} a_A t^2 = \dfrac{1}{8} g t^2
x A ( t ) = 2 1 a A t 2 = 8 1 g t 2
時刻 t = t 1 t = t_1 t = t 1
x A ( t 1 ) = 1 8 g t 1 2 = l
x_A (t_1) = \dfrac{1}{8} g t_1^2 = l
x A ( t 1 ) = 8 1 g t 1 2 = l
∴ t 1 = 2 2 l g
\therefore t_1 = 2 \sqrt{2} \sqrt{\dfrac{l}{g}}
∴ t 1 = 2 2 g l
と求められます。
(6)
時刻 t = t 1 t = t_1 t = t 1 v A ( t 1 ) v_A (t_1) v A ( t 1 )
v A ( t 1 ) = 1 4 g t 1 = 1 4 g 2 2 l g = 1 2 g l
\begin{aligned}
v_A (t_1) &= \dfrac{1}{4} g t_1 \\
&= \dfrac{1}{4} g 2 \sqrt{2} \sqrt{\dfrac{l}{g}} \\
&= \dfrac{1}{\sqrt{2}} \sqrt{g l}
\end{aligned}
v A ( t 1 ) = 4 1 g t 1 = 4 1 g 2 2 g l = 2 1 g l
となります。
(7)
物体 A・B の系で考えます。物体 A と B の衝突によりお互いが与え合う力は,この系では内力となるため,衝突前後では運動量が保存されます (運動量保存則とエネルギー保存則の導出 )。
したがって,衝突直後の物体 B の速度を v B 0 v_B^0 v B 0
m v A ( t 1 ) + M ⋅ 0 = m ⋅ 0 + M v B 0
m v_A (t_1) + M \cdot 0 = m \cdot 0 + M v_B^0
m v A ( t 1 ) + M ⋅ 0 = m ⋅ 0 + M v B 0
∴ v B 0 = m M v A ( t 1 ) = 1 2 m M g l
\therefore v_B^0 = \dfrac{m}{M} v_A (t_1) = \dfrac{1}{\sqrt{2}} \dfrac{m}{M} \sqrt{g l}
∴ v B 0 = M m v A ( t 1 ) = 2 1 M m g l
のように求められます。
(8)
物体 B が動き出したあと,等速直線運動をすることより,斜面に水平な方向でも力のつりあいが成り立つことがわかります。
物体 B に加わる垂直抗力および動摩擦力を f B ′ , N B f_B', N_B f B ′ , N B
{ 水平: M g sin π 6 = 1 2 M g = f B ′ 鉛直: N B = m g cos π 6 = 3 2 M g
\begin{cases}
\text{水平}:Mg \sin{\dfrac{\pi}{6}} = \dfrac{1}{2} Mg = f_B' \\
\text{鉛直}:N_B = mg \cos{\dfrac{\pi}{6}} = \dfrac{\sqrt{3}}{2} Mg
\end{cases}
⎩ ⎨ ⎧ 水平 : M g sin 6 π = 2 1 M g = f B ′ 鉛直 : N B = m g cos 6 π = 2 3 M g
斜面と物体 B との間の動摩擦係数を μ B ′ \mu_B' μ B ′ f B ′ = μ B ′ N B f_B' = \mu_B' N_B f B ′ = μ B ′ N B
1 2 M g = μ B ′ 3 2 M g
\dfrac{1}{2} Mg = \mu_B' \dfrac{\sqrt{3}}{2} Mg
2 1 M g = μ B ′ 2 3 M g
∴ μ B ′ = 1 3
\therefore \mu_B' = \dfrac{1}{\sqrt{3}}
∴ μ B ′ = 3 1
と求められます。
問3
(9)
物体 A が物体 B と衝突してからの時刻を t ′ t' t ′
時刻 t ′ t' t ′ x B ( t ′ ) x_B (t') x B ( t ′ )
x B ( t ′ ) = v B 0 t ′ = 1 2 m M g l t ′
x_B (t') = v_B^0 t' = \dfrac{1}{\sqrt{2}} \dfrac{m}{M} \sqrt{g l} t'
x B ( t ′ ) = v B 0 t ′ = 2 1 M m g l t ′
物体 B が斜面の下端点 O に達するまでの時間 t ′ = t 1 ′ t' = t'_1 t ′ = t 1 ′
d = 1 2 m M g l t 1 ′
d = \dfrac{1}{\sqrt{2}} \dfrac{m}{M} \sqrt{g l} t'_1
d = 2 1 M m g l t 1 ′
∴ t 1 ′ = 2 M m d g l
\therefore t'_1 = \sqrt{2} \dfrac{M}{m} \dfrac{d}{\sqrt{g l}}
∴ t 1 ′ = 2 m M g l d
これより,物体 A がすべり始めてから物体 B が斜面の下端点 O に達するまでに要する時間 T T T
T = t 1 + t 1 ′ = 2 2 l g + 2 M m d g l = 2 l g ( 2 + M m d l )
\begin{aligned}
T &= t_1 + t'_1 \\
&= 2 \sqrt{2} \sqrt{\dfrac{l}{g}} + \sqrt{2} \dfrac{M}{m} \dfrac{d}{\sqrt{g l}} = \sqrt{2} \sqrt{\dfrac{l}{g}} \left( 2 + \dfrac{M}{m} \dfrac{d}{l} \right)
\end{aligned}
T = t 1 + t 1 ′ = 2 2 g l + 2 m M g l d = 2 g l ( 2 + m M l d )
と求められます。
(10)
この運動で失った力学的エネルギー Δ E \Delta E Δ E E ( 0 ) E (0) E ( 0 ) E ( T ) E (T) E ( T )
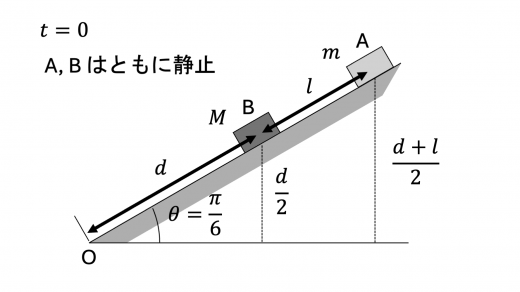
上図より,E ( 0 ) E (0) E ( 0 )
E ( 0 ) = m g ( d + l ) sin π 6 + M g d sin π 6 = 1 2 [ m g ( d + l ) + M g d ]
E(0) = mg (d + l) \sin{\dfrac{\pi}{6}} + Mg d \sin{\dfrac{\pi}{6}} = \dfrac{1}{2} [mg (d + l) + Mg d]
E ( 0 ) = m g ( d + l ) sin 6 π + M g d sin 6 π = 2 1 [ m g ( d + l ) + M g d ]
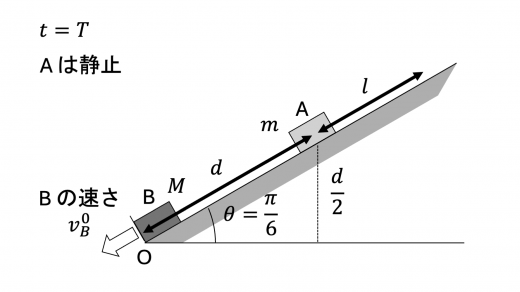
また上図より E ( T ) E (T) E ( T )
E ( T ) = m g d sin π 6 + 1 2 M ( v B 0 ) 2 = 1 2 m g d + 1 4 ( m M ) 2 M g l
\begin{aligned}
E (T) &= mg d \sin{\dfrac{\pi}{6}} + \dfrac{1}{2} M (v_B^0)^2 \\
&= \dfrac{1}{2 } mg d + \dfrac{1}{4} \left( \dfrac{m}{M} \right)^2 Mgl
\end{aligned}
E ( T ) = m g d sin 6 π + 2 1 M ( v B 0 ) 2 = 2 1 m g d + 4 1 ( M m ) 2 M g l
したがって,Δ E \Delta E Δ E
Δ E = E ( 0 ) − E ( T ) = 1 2 M g d + 1 4 ( 2 − m M ) m g l
\begin{aligned}
\Delta E &= E(0) - E (T) \\
&= \dfrac{1}{2} Mg d + \dfrac{1}{4} \left( 2 - \dfrac{m}{M} \right) mgl
\end{aligned}
Δ E = E ( 0 ) − E ( T ) = 2 1 M g d + 4 1 ( 2 − M m ) m g l
のように表されます。
(11)
この失われたエネルギーは,物体 A の運動で失われたエネルギー Δ E A \Delta E_A Δ E A Δ E B \Delta E_B Δ E B Δ E c \Delta E_c Δ E c
まず,E A ( 0 ) E_A (0) E A ( 0 ) f A ′ f_A' f A ′ l l l Δ E A \Delta E_A Δ E A
Δ E A = f A ′ l = μ 2 N A l = 1 2 3 m g 3 2 l = 1 4 m g l
\begin{aligned}
\Delta E_A &= f_A' l \\
&= \dfrac{\mu}{2} N_A l \\
&= \dfrac{1}{2 \sqrt{3}} mg \dfrac{\sqrt{3}}{2} l \\
&= \dfrac{1}{4} mgl
\end{aligned}
Δ E A = f A ′ l = 2 μ N A l = 2 3 1 m g 2 3 l = 4 1 m g l
と求められます。
(12)
次に,Δ E B \Delta E_B Δ E B f B ′ = μ B ′ N B f_B' = \mu_B' N_B f B ′ = μ B ′ N B d d d
Δ E B = μ B ′ N B d = 1 3 M g 3 2 d = 1 2 M g d
\begin{aligned}
\Delta E_B &= \mu_B' N_B d \\
&= \dfrac{1}{\sqrt{3}} Mg \dfrac{\sqrt{3}}{2} d \\
&= \dfrac{1}{2} Mg d
\end{aligned}
Δ E B = μ B ′ N B d = 3 1 M g 2 3 d = 2 1 M g d
(13)
(11)での議論により,物体 A・B の衝突により失われたエネルギー Δ E c \Delta E_c Δ E c
Δ E c = Δ E − Δ E A − Δ E B
\Delta E_c = \Delta E - \Delta E_A - \Delta E_B
Δ E c = Δ E − Δ E A − Δ E B
により求められます。
(10)・(11)・(12)の結果を代入して
Δ E c = 1 2 M g d + 1 4 ( 2 − m M ) m g l − 1 4 m g l − 1 2 M g d = 1 4 ( 1 − m M ) m g l
\begin{aligned}
\Delta E_c &= \dfrac{1}{2} Mg d + \dfrac{1}{4} \left( 2 - \dfrac{m}{M} \right) mgl - \dfrac{1}{4} mgl - \dfrac{1}{2} Mg d \\
&= \dfrac{1}{4} \left( 1 - \dfrac{m}{M} \right) mgl
\end{aligned}
Δ E c = 2 1 M g d + 4 1 ( 2 − M m ) m g l − 4 1 m g l − 2 1 M g d = 4 1 ( 1 − M m ) m g l
と求められます。
(13)の補足
(13)の結果より,物体 A・B の衝突でエネルギーが失われない条件は,Δ E c = 0 \Delta E_c = 0 Δ E c = 0 m = M m = M m = M
一方,物体 A・B の衝突でエネルギーが失われない条件 (v A , v B v_A, v_B v A , v B
m v A + M ⋅ 0 = m ⋅ 0 + M v B
m v_A + M \cdot 0= m \cdot 0 + M v_B
m v A + M ⋅ 0 = m ⋅ 0 + M v B
さらに弾性衝突をすることより
v B − 0 = − 1 ( 0 − v A )
v_B - 0 = -1 (0 - v_A)
v B − 0 = − 1 ( 0 − v A )
∴ v B = v A ( ≠ 0 )
\therefore v_B = v_A (\neq 0)
∴ v B = v A ( = 0 )
運動量保存則の条件より,結局物体 A・B の衝突でエネルギーが失われない条件として
m = M
m = M
m = M
が得られます。
失われたエネルギーからの導出はこの議論の結果と一致しています。
終盤は d d d l l l