【解答・解説】東工大物理2025 第1問 -力学-
2025年度の東科大物理第1問を解説します。力学の単元です。
この記事に関連するQ&A
問題
問題
以下の問題文および図は,2025年度東京科学大学入試問題物理第1問から引用しています(一部見やすさ等のためライターが修正・変更した部分があります)。
図1に示すような円錐状にくり抜かれた台の上における物体の運動について考える。
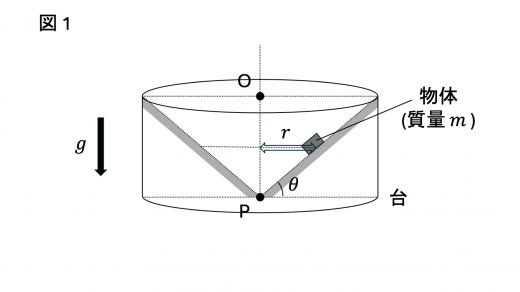
円錐の底面の中心を点 O,頂点を点 P とし,線分 OP は鉛直方向に沿っているとする。また,円錐の母線が線分 OP に垂直な面となす角を とする。物体は質量 の質点とみなせるものとする。台と物体との間には摩擦があり,静止摩擦係数を ,動摩擦係数を とする。台は線分 OP を軸として回転することができるが,並進はしないものとする。鉛直下向きの重力加速度の大きさを とする。以下の設問に答えよ。
[A] 台が回転していない状況を考える。はじめ,物体は線分 OP から だけ離れた台上の点で静止している。
(a) 物体にはたらく摩擦力の大きさ を求めよ。
物体に対して点 P へ向けて指で少しずつ力を加えたところ,物体は指を離れて台に対して初速度 で点 P に向かって滑り出し,やがて点 P に到達した。
(b) 物体が点 P に到達した際の速さ を求めよ。
© 物体が指を離れてから点 P に到達するまでに摩擦力が物体に対してした仕事 を, のうち必要なものを用いて表せ。
[B] 物体が線分 OP から だけ離れた台上の点で静止している状態で,図2に示すように,台を真上から見て反時計回りにゆっくりと回転させ始めた。
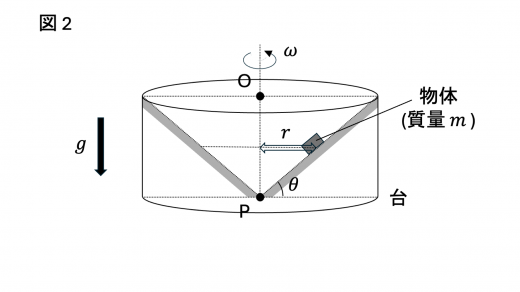
回転の角速度 を から少しずつ大きくしたところ,ある角速度 に達した時点で物体は台に対して滑り出した。角速度の時間変化は無視できるものとする。
(d) 角速度 で台を回転させている間に,物体にはたらく垂直抗力の大きさ を求めよ。
(e) 台上の観測者から見て物体が滑り出す向きとして,最も適当なものを図3の ①〜⑧ から 1 つ選べ。なお,②,④,⑥,⑧ はそれぞれ,① と ③,③ と ⑤,⑤ と ⑦,⑦ と ① に挟まれた任意の向きを示す。
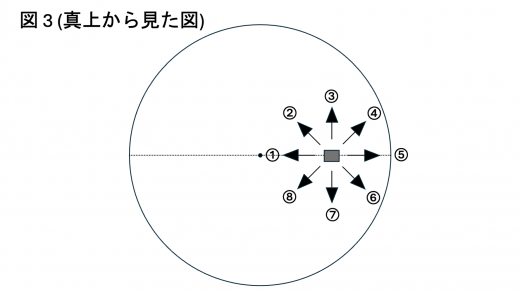
(f) 物体が台に対して滑り出した時点における台の回転の角速度 を求めよ。
[C] 物体が線分 OP から だけ離れた台上の点で静止している。微小な時間 に対し の割合で回転の角速度 を から大きくしながら台を真上から見て反時計回りに回転させ始めたところ,回転させ始めると同時に物体は台に対して滑り始めた。
(g) 微小な時間 における,線分 OP から だけ離れた台上の速さの変化 を求めよ。
(h) 台上の観測者から見て物体が滑り出す向きとして,最も適切なものを図3の ①〜⑧ より 1 つ選べ。なお,②,④,⑥,⑧ はそれぞれ,① と ③,③ と ⑤,⑤ と ⑦,⑦ と ① に挟まれた任意の向きを示す。
(i) 回転させ始めると同時に物体が台に対して滑り出すために, が満たすべき条件を不等式で示せ。
円運動 (円運動とは|円運動における加速度・向心力・遠心力) に関する問題です。[A],[B] は通常の円運動に関する標準的な問題ですが,[C] は角振動数が等加速度で変化する場合の問題であり,あまり見慣れない問題かもしれません。
解答例
解答例
以下では,物体にはたらく力を図示した図が出てきますが,見やすさのため,力の作用点などはずらして書かれていることがあります。
A
(a)
物体にはたらく力を図示してみます。
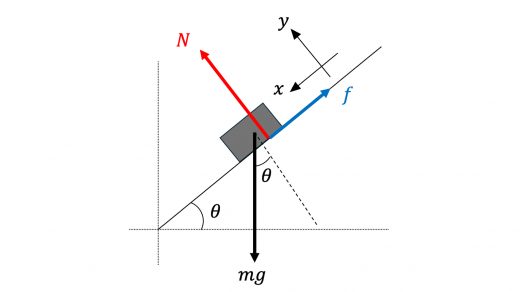
上図のように 軸をとると,各方向に対して力のつりあいより
これより
と求められます。
また,垂直抗力に関しては と求められます。
(b)
物体が運動しているときの運動方程式を考えます。 軸方向には物体は静止したままなので,物体にはたらく垂直抗力は前問で求めた となります。 軸方向の加速度を とすると
初速度 ,初期位置を原点とすると,時刻 での物体の速度 および位置 は,等加速度運動の公式 (等加速度運動・等加速度直線運動の公式) より
時刻 で物体が点 O に到達するとします。図1より なので
時刻 での物体の速さが求める速さ であり
となります。
(別解) 等加速度運動の公式
を用います。 物体が点 P に到達したときの速さは ,位置は なので,
と求められます。
©
物体が点 P に到達するまでの間,摩擦力の大きさは で一定です。摩擦力の運動に対する向きを考えて,求める仕事 は
と求められます。
(別解) エネルギー保存則 (熱力学第一法則|仕事と内部エネルギーの関係) より,物体の力学的エネルギーの変化が,摩擦力のした仕事 となります。したがって,点 P を位置エネルギーの基準として
と求められます。
B
(d)
角速度 のとき,台と同時に回転運動する系からみたときの,物体にはたらく力を図示します。遠心力がはたらくことに注意してください。
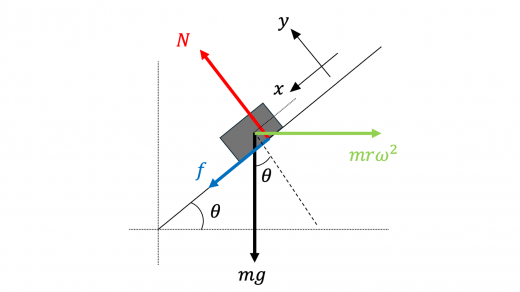
軸方向での力のつりあいより
と求められます。
(e)
摩擦力の向きについて考えます。角速度 を上げていくと,遠心力も大きくなっていき,ある角速度 で物体が滑り出すことから,摩擦力は 軸正の向きにはたらくことがわかります。
これより台上の観測者から見て物体が滑り出す向きとして適切な方向は ⑤ とわかります。
(f)
物体が台に対して静止しているときの静止摩擦力の大きさ を求めます。これは,力のつりあいより
のとき, が成り立ちます (摩擦力の定義|動摩擦力・静止摩擦力・摩擦係数の解説)。すなわち
のように求められます。
C
(g)
時刻 で物体の速さが に変化したとします。このとき,OP から だけ離れた点の速さは,円運動の速さの公式より
となります。
(h)
回転座標における一般の円運動では,遠心力のほかにコリオリ力とオイラーの力がはたらきます (コリオリの力の導出)。
回転させ始めた瞬間,台の角速度および物体の速度は なので,この3つの力のうち,遠心力とコリオリ力ははたらかず,オイラーの力のみがはたらきます。このオイラー力の向きは回転と逆向きにはたらきます。
したがって,台上の観測者から見たとき,物体にはたらく力は重力,垂直抗力,摩擦力,オイラーの力となります。
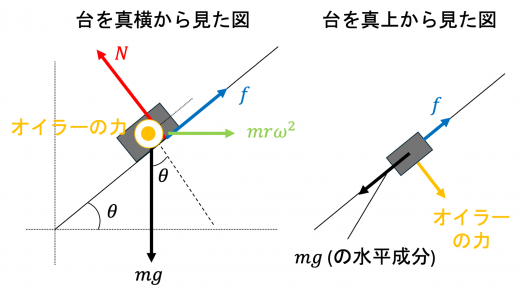
したがって,台上の観測者から見て物体が滑り出す向きは,重力の水平方向の成分 (と摩擦力) とオイラーの力の合力の向きとなるので,⑧ となります。
(i)
物体が静止しているときの静止摩擦力の大きさ が最大静止摩擦力 より大きければ,台が回転し始めると同時に物体が台に対して滑り出します。
まず, について求めます。オイラーの力の大きさは として与えられるので, は
と求められます。
次に,垂直抗力の大きさ は,これまで用いてきたように となります。
より
より両辺正としてよいから,結果として
を得ることができます。
[A],[B] は完答したい問題です。











