【解答・解説】京大物理2024 第3問 -波動-
2024年度の京大物理第3問を解説します。波動の単元です。
この記事に関連するQ&A
問題
問題
以下の問題文および図は,2024年度京都大学入試問題物理第3問から引用しています(一部見やすさ等のためライターが修正・変更した部分があります)。
次の文章を読んで, に適した式または数値を,{ } からは適切なものを一つ選びその番号を,それぞれの解答欄に記入せよ。なお, はすでに で与えられたものと同じものを表す。また,問1では,指示にしたがって,解答を解答欄に記入せよ。ただし,円周率を とする。
物質中を光が進むときのふるまいを考え,それを応用した光ファイバーなどについて考察しよう。以下では空気の屈折率を1とする。
(1) 図1のように屈折率が の物質 A と屈折率が の物質 B が平らな面で接しており, とする。A から B へ光が入射したとき,境界面の法線に対する角度として,入射角 ,反射角 ,屈折角 を定める。
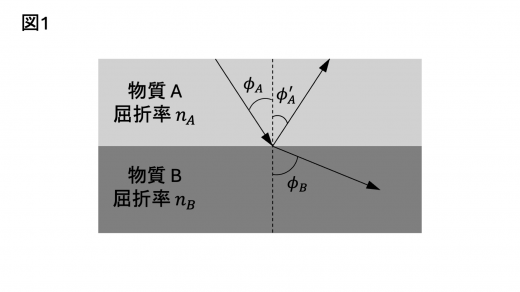
であり, の関係は となる。 がある値 より大きいとき,光は境界面で全反射される。 と の関係は である。
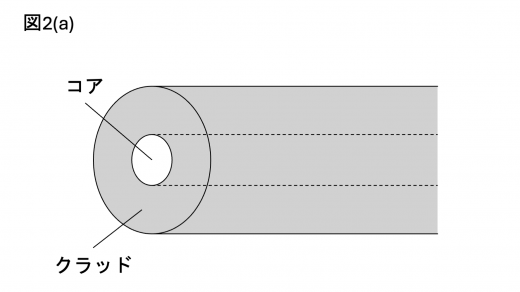
(2) 光ファイバーは,図2(a)のように屈折率の異なるガラスを同軸状の細線にしたものである。中心部分をコア,外側部分をクラッドと呼ぶ。コアとクラッドの屈折率をそれぞれ とする。また,コアの軸を含む平面内を進む光を考える。
屈折率の関係が {え:① ,② ,③ } で,さらにコア内で光の進む方向と光ファイバーの軸方向のなす角度 がある角度 より小さければ,図2(b)のように光はコアとクラッドの境界で全反射される。
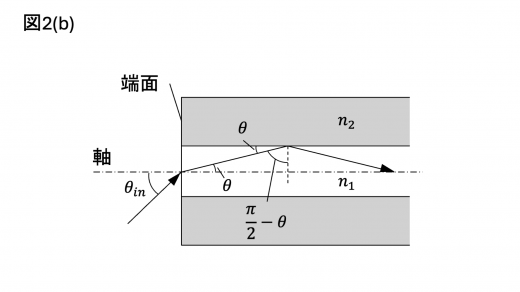
(1)での議論をふまえると, と および の関係は となる。このように光がコアとクラッドの境界面で全反射されるためには,光ファイバーの端面において空気中からコアに光が入射する際に,軸方向に対する光の入射角 がある条件を満たす必要がある。その条件を, を用いて表すと, となる。ただし,光ファイバーの端面はその軸方向に対して垂直であるとし,端面においてコアの軸上から入射する光を考えよ。
(3) 入射した光が光ファイバー内を進むためには,(2)の条件だけでは不十分である。それを考察しよう。
コアの軸を含む平面内を進む光を考える。図3のように,コア中の光の波長を とし,光の進行方向とコアの軸方向のなす角度を とする。
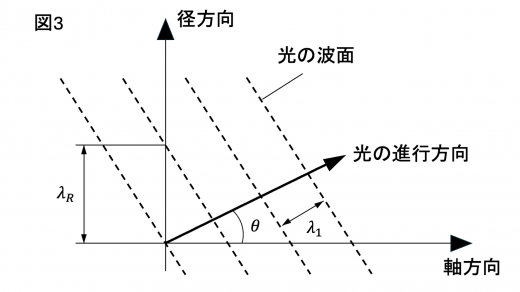
このとき,径方向の波面間の距離を とすると, となっている。したがって,径方向には波長が の波が生じているとみなせる。
半径 のコア内で光が弱まらずに進んでいくとき,径方向には定在波が形成されている。ここでは,議論を簡単にするため,自然数 に対し,コアの直径が の 倍であればそのような定在波が形成されるとする。このとき, を用いて, と表される。
実際に光ファイバーを使う際には,空気中での波長が の光をレンズ等で集光してコアに入射させるため,光はさまざまな で入射し,入射直後の は連続的な値を持ち得る。そのうち を満たすとびとびの値の を持つ光だけがコア内を進むことができる。 で特徴づけられるこの光をモードとよぶ。一方,ある のモードについて, がある値 より大きいとき,このモードはコアとクラッドの境界で全反射できず伝わらなくなる。 を を用いて表すと, となる。ここで, の関係を用いよ。 が を満たすとき,コア内を伝わる光は のモードのみとなる。下限 はカットオフ波長とよばれ, を用いて と表せる。
(4) 以下では, のモードだけが伝わる場合を考える。コア内の波長が の光は,図4のような波の合成の結果,軸方向と垂直な波面をもつ波とみなせる。また, が小さい場合を考え,合成された光の波長は と等しいとする。
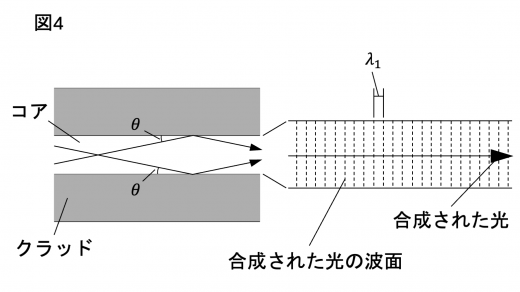
図5のように,光ファイバーのコアに,光を散乱する構造を周期的に軸方向に導入したものを考える。これをファイバー・ブラッグ・グレーティング (FBG) という。この構造の周期を とすると,FBG は間隔 の回折格子のようにはたらく。すなわち,入射した光のごく一部が散乱されて入射側へと返っていくが,たがいに 離れた位置からの散乱光が強め合うとき強い光が返っていき,図5の検出器で検出することができる。
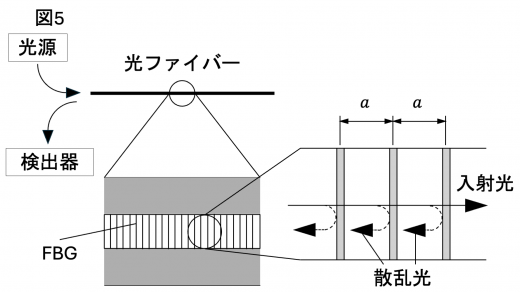
軸方向に返っていく光が強め合う条件から,検出できる光の最も長い波長は, を用いて と表すことができる。検出器が検出するのは空気中の波長であることに注意せよ。以下では強め合って返っていく光のうち波長が の光を考え,これを反射光とよぶ。
(5) FBG を含む光ファイバーの一部分を考える。これが長さ の状態から とくらべて十分に小さい量 だけ一様に変化し,長さが になると,FBG の周期も から に変化する。この場合, の関係は である。また,この周期の変化により,FBG からの反射光の波長も から に変化する。光の波長は高感度に計測できるため,FBG は微小な伸縮を検出するセンサーとして利用できる。ここで, を定数として, とおく。 は,伸縮にともなう FBG 内のコアの屈折率の微小な変化の影響などを含んだ係数である。
を決定するため, の光ファイバーに波長が 1500 nm 付近の連続スペクトルの光を導入し,FBG を含む部分の長さを 10.00 mm から変化させながら,FBG からの反射光の強度と波長の関係を空気中で測定した。すると,図6の結果が得られた。
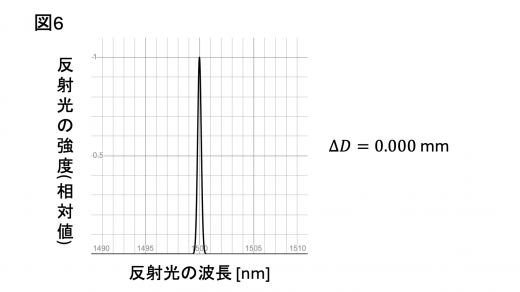
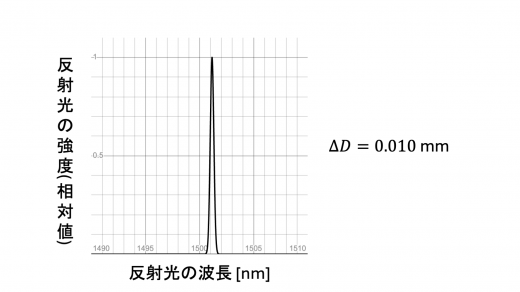

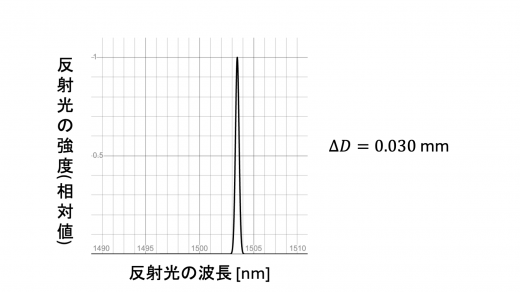
この結果から係数 は有効数字1桁で と求めることができる。
FBG の応用例の一つに,熱膨張測定がある。固体物質の長さを ,絶対温度を とすると,多くの物質は室温付近において という関係を示す。係数 は線膨張率, は室温に近い基準温度, は での長さである。
上述の FBG を,長さ 20.0 mm の固体物質 X の試料に図7(a)のように貼り付けた。X は一様に熱膨張し,光ファイバーは X の熱膨張に完全に追随して伸縮すると仮定する。また,温度変化による の変化は微小である。FBG に空気中での波長が 1500 nm 付近の連続スペクトルの光を導入すると,基準温度において 1500.00 nm の光が反射され,温度を変えながら反射光の空気中での波長の変化を測定した結果,図7(b)が得られた。ただし,試料の熱膨張以外に起因する波長の変化は差し引いてある。
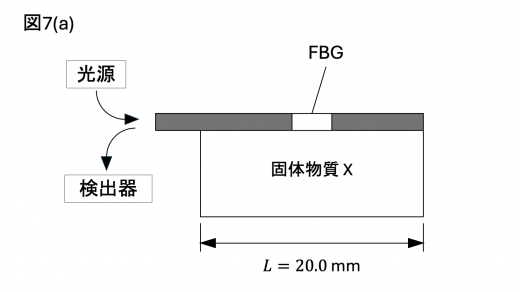
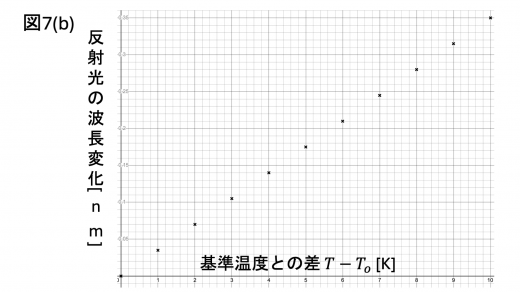
表1は X の候補物質とそれらの線膨張率である。
表1
| 物質名 | 線膨張率 [ / K] |
|---|---|
| 白金 | 8.8 |
| 銀 | 18.9 |
| 亜鉛 | 30.2 |
問1 実験結果と の値を用い,X が表1のどの物質かを推定せよ。議論の過程も示せ。
光の全反射の性質を用いて物質の同定を行う実験について,考察する問題です。
解答例
解答例
(1)
入射角 と反射角 との間には,反射の法則 (反射の法則・屈折の法則) より
という関係が成り立ちます (あ:)。
また,物質 A から物質 B に光が入射していくとき,入射角 ,屈折角 およびそれぞれの物質の屈折率 との間には,屈折の法則より
が成り立ちます (い:)。
となるとき, となり,光が境界面で全反射 (全反射の要点と, 臨界角の計算方法) されます。このような は,屈折の法則より
と表されます (う:)。
(2)
の取り方に注意してください。
コアからクアッドに入射する光が全反射されるような入射角 は,(1)での議論より
このような角度 が存在する条件は,
と求められます (え:①)。
と考えてよいので,上式より, は
と表されます (お:)。
空気中からコアに入射した光が,コアとクラッドの境界面で全反射されるための,空気中からコアに入射する光の入射角 の条件を求めます。屈折の法則より
コアとクラッドの境界面で全反射されるための条件は であったので, より
となります (か:)。
(注)空気中からコアに入射した光が全反射しないことも,条件としては必要です。空気中からコアに入射した光が全反射するような入射角を とすると,(1)での議論より
となります。一方, より,条件 を満たす角度 について
が成り立っています。いま であるので, が成り立ちます。したがって,条件 が成り立っていれば,全反射も起こりません。
(3)
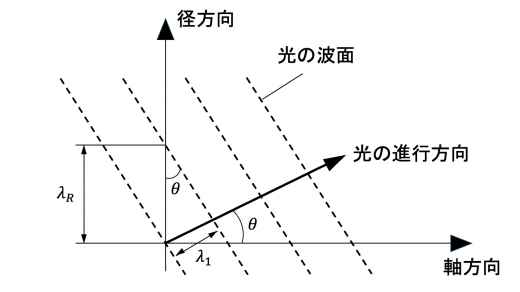
上図のように,光の進行方向とコアの軸方向のなす角度が であるとき,コア中の光の波長 と径方向の光の波面間の距離 との間には
という関係が成り立っています (き:)。
径方向に定在波 (あるいは定常波 (定常波・合成波・重ね合わせの原理)) が存在していると考えます。問題文より光の強め合いの条件は
となります (く:)。
空気中の光の波長 とコア内の光の波長 との間には,屈折の法則より
という関係があることを用いると,この条件はさらに
と表されます。
このように,強め合う光について, で特徴づけられるモードについて考えます。
ある のモードについて, となると,この光はコアとクラッドの境界で全反射できなくなってしまいます。これは, のとき, となっていると考えられます。したがって
と求められます (け:)。
さらに, の具体的な値を代入すると
と表すこともできます。
カットオフ波長 は,上式に を代入して
と表されます (こ:)。
(4)
FBG を間隔 の回折格子とみなし,この回折格子での光の散乱を考えます。たがいに だけ離れた位置からの散乱光が強め合う条件を考えます。
図5右図において,たがいに だけ離れた光の経路差は であるとわかります。この距離がコア内の波長の整数倍のとき,これらの光は強め合います (波の干渉・回折)。
したがって,強め合いの条件は,整数 を用いて
検出できる光の最も長い (空気中の) 波長は のときの波長で
となります (さ:)。
以下では問題文に倣って,この波長の光を反射光と呼びます。
(5)
FBG の長さと周期が変化しても,周期の繰り返しの回数は変化しません。したがって, の間には
という関係が成り立ちます (し:)。
この周期の変化により反射光の波長も から に変化します。このとき波長の変化と周期の変化に
という関係が成り立つとして,図6の実験データから係数 を決定します。しより
であることに注意します。
4つのプロットのうち最下段のものに着目します。このとき 0.030 mm,またプロットより 3.5 nm と読み取れるので,上式に代入して
有効数字1桁では と求められます (す:0.8)。
問1
熱膨張の公式より,温度による試料の長さの変化を とすると
光ファイバーは試料 X の熱膨張に完全に追随して伸縮することより
と考えてよいので,FBG の反射光の波長変化の公式より,反射光の波長変化と試料の長さの変化との間には
という関係があることがわかります。
図7(b)のプロットはこれに従う直線となっていることが確かめられます。この直線の傾きを求めます。プロットの原点および 10[K] の点で 0.35 nm であることより
この結果より,試料 X は 亜鉛 であると推定されます。
問題文をよく読みながら,丁寧に解答しましょう。物理の実験の面白さを味わえる問題になっています。











