【解答・解説】京大物理2024 第2問 -電磁気-
2024年度の京大物理第2問を解説します。電磁気の単元です。
この記事に関連するQ&A
問題
問題
以下の問題は,2024年度京都大学入試問題物理第2問から引用しています(一部修正しています)。
なお,本記事中の図は全て,2024年度京都大学入試問題物理第2問を参考に,ライターが作成したものです(一部見やすさ等のためライターが変更した部分があります)。
次の文章を読んで, に適した式または数値を,{ } からは適切なものを一つ選びその番号を,それぞれの解答欄に記入せよ。なお, はすでに で与えられたものと同じものを表す。また,問1〜問3 では,指示にしたがって,解答をそれぞれの解答欄に記入せよ。ただし,円周率を とする。
(1) 図1のように, 軸上に置かれた十分に長い直線状の導線に, 軸正の向きに強さ の定常電流が流れている場合を考える。
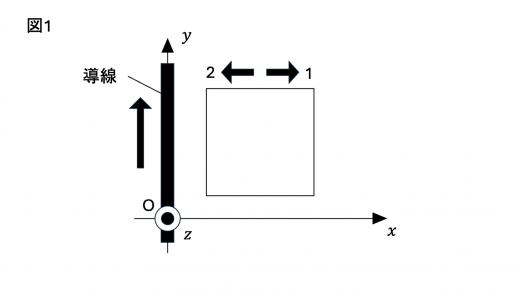
真空の透磁率を とすると,この電流がつくる磁束密度の大きさは, 軸から距離 離れた点で となる。 平面上の の領域に,正方形の1巻きコイルを置く。図1に示すように,各辺は 軸あるいは 軸に平行である。ただし,コイルの自己インダクタンスは無視できるものとする。コイルが 軸の正の向きに一定の速さで動くとき,誘導電流は {ロ:①図の 1 の向きに流れる,②図の 2 の向きに流れる,③流れない}。また,コイルが 軸の正の向きに一定の速さで動くとき,誘導電流は {ハ:①図の 1 の向きに流れる,②図の 2 の向きに流れる,③流れない}。
(2)次に,非一様な磁場中での荷電粒子の運動を考えよう。荷電粒子の大きさは無視でき,その質量は ,電荷は とする。簡単のため,図2に示すようなモデルで考える。
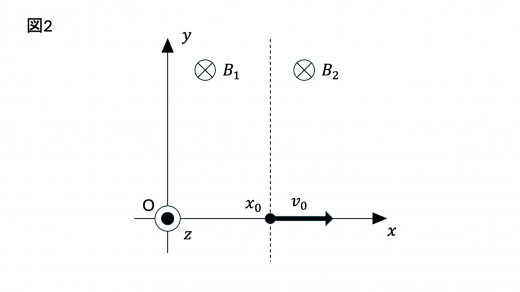
磁場は 軸負の向きにかかっており,その磁束密度の大きさは,ある に対して, で , で とする。ただし と は正の定数で, である。また,粒子が で定められる平面を通過するとき,その軌道は滑らかにつながり,速さは変化しないとする。
時刻 で にある荷電粒子が, 軸正の向きに速さ で運動をはじめた。荷電粒子はまず, の領域においてローレンツ力により 平面内で等速円運動する。 での円軌道の半径は となる。荷電粒子が ではじめて に到達するまでかかる時間 は, のうち必要なものを用いて と書ける。その後,粒子は においても等速円運動する。 からふたたび に到達するまでの時間を とし, を運動の周期とする。
問1 時刻 から時刻 までの荷電粒子の 平面内での起動を描き,時刻 における位置を示せ。また,時刻 での位置を始点とし, での位置を終点とするベクトルについて,その大きさを答えよ。このベクトルで表される移動をドリフトと呼ぶ。
問1で考察したドリフトについて,その平均の速さを求めよう。磁束密度の大きさを正の定数 および を用いて と与える。運動の周期 を のうち必要なものを用いて書くと となる。ドリフトの平均の速さは,ドリフトを表すベクトルの大きさを周期で割ることによって求められ, のうち必要なものを用いて と書ける,一般に,一様でない磁場がある場合にこのようなドリフトが生じ,これは磁場勾配ベクトルとよばれる。
次に,図3のように,粒子が時刻 で にあり, 平面内で 軸に対する角度が の方向に速さ で運動をはじめる場合を考える。
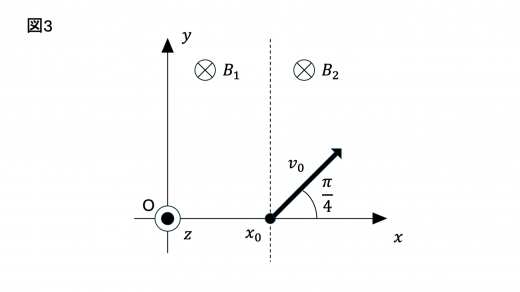
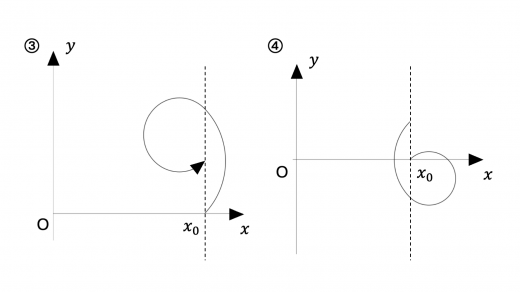
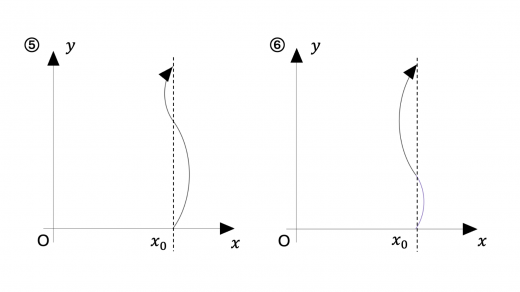
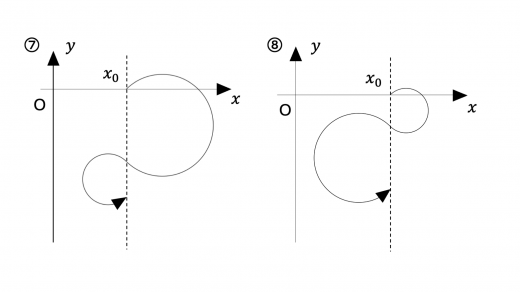
問2 から, で2回目の に達するときまでの粒子の軌道として最も適切なものを図4の①〜⑧から選び,番号を答えよ。
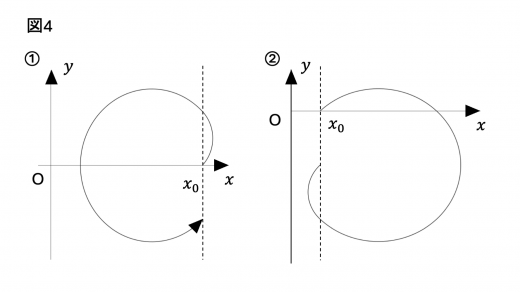
(3) 次に,一様な磁場のもとで,ローレンツ力に加えて外力が荷電粒子にはたらく場合を考えよう。荷電粒子は質量 ,電荷 をもち,磁束密度の大きさを正の定数 とする。さらに,粒子には 軸の正の向きに大きさ の一様な保存力である外力が作用する。磁場および外力はいずれも時間変動しない。
このとき,荷電粒子は 軸方向には一定の範囲で周期的に振動する。運動中にある時刻で粒子が, が最小値 となる位置にあり速さ をもっていたとすると, が最大値 となる位置まで移動したときの速さ は,この間に外力がした仕事 が正であるため より大きくなる。その後 にもどったとき,粒子の速さは に比べて {チ:①大きくなる,②小さくなる,③変化しない}。
ローレンツ力に対して外力が十分に弱いとき,荷電粒子の運動の等速円運動からのずれはわずかである。以下では,図6のように,(2)と同様に の領域と の領域に分け,この粒子の運動を, 平面内のそれぞれの領域で,異なる速さで等速円運動するモデルで考察する。
荷電粒子は磁場によるローレンツ力をうけ, で速さ , で速さ の等速円運動を行うとする。ここで, である。外力により と の差が生じ,それ以外には外力による運動への影響はないと仮定する。また, で粒子の軌道は滑らかにつながるとする。ただし,解答に および は,用いないこと。
時刻 で にある荷電粒子が 軸の正の向きに速さ で等速円運動をはじめた。 における等速円運動の円の半径は となり,時刻 で2回目に に達するまでの時間 は となる。時刻 での粒子の位置を始点, での位置を終点とするベクトルがこの場合のドラフトを表す。このベクトルの向きから, 軸の負の向きの磁場および 軸正の向きの外力によって {ル:① 軸正,② 軸の正,③ 軸の負,④ 軸の負} の向きにドリフトを生じることがわかる。このドリフトの平均の速さは,そのベクトルの大きさを周期 で割り, を用いずに と求められる。このモデルでは, と の各領域における円軌道の半径をそれぞれ とすると,粒子が 軸方向に と の間を移動する。 と の違いによる運動エネルギーの差が と等しいとすると, は, のうち必要なものを用いて と表すことができる。
問3 一様な外力が強さ の電場による力の場合, として, のドリフトの平均の速さを求めよ。また,時刻 から までの荷電粒子の 平面内での軌道を描け。さらに,同じグラフに電荷が の場合の軌道を2周期ぶん描け。ただし,どちらも において上の条件で運動をはじめるものとする。それぞれの軌道に電荷の値を明示し,始点と終点の違いがわかるように描くこと。
ここでは簡単なモデルによって考察したが,正確なドリフトの速さは の定数倍であり,このような簡単なモデルでも,ドリフトの特性を得ることができる。
ドリフトとよばれる現象について考察する問題です。
解答例
解答例
(1)
軸の導線を強さ の電流が流れているとき, 軸から距離 だけ離れた点での磁束密度の大きさ は,磁束密度の公式 (電流と磁束密度の関係) より
となります。
平面の第1象限に正方形状のコイルを置き,そのコイルを通る磁束について考えます。まず,コイルが 軸正の向きに一定の速さで運動するときを考えます。このとき,コイルとその内部の各点と 軸 との距離は不変なので,コイルを通る磁束の大きさは変わりません。したがって,ファラデーの電磁誘導の法則 (電磁誘導とレンツの法則) より,このコイルに誘導電流は流れません (ロ:③)。
次に,コイルが 軸正の向きに一定の速さで運動するときを考えます。このとき,時間変化に対してコイルとその内部の各点と 軸 との距離は変化するので,コイルを通る磁束の大きさは時間変化することになります。したがって,ファラデーの電磁誘導の法則により,このコイルには誘導電流が流れることになります。この誘導電流の向きについて考えます。いま, 平面の第1象限には 軸負の方向に磁場が発生しています。その大きさは (イ) で表されるため,コイルが 軸正の向きに一定の速さで運動するとき,コイルとその内部の各点における磁束密度の大きさは減少します。したがって,レンツの法則 (電磁誘導とレンツの法則) より, 軸負の方向の磁束を増やす方向に誘導電流が流れるので,誘導電流は図1の1の向きに流れるとわかります (ハ:①)。
正方形コイルのうち原点 O に最も近い点の座標を A,各辺の長さを とします。
このときコイルを通る磁束 ( 軸負の向きを正とする) は
いま, 平面内においては, となるので
この多重積分は ごと, ごとに計算することができるので
すなわち, は点 A の 座標 と辺の長さ に依存し,点 A の 座標 には依存しないことがわかります。また, は に対して単調に減少することより, は が大きくなると小さくなることがわかります。
コイルが一定の速さ で 軸正の向きに時刻 だけ進むと,A の座標は と変化します。したがってこのコイルの移動に対して は変化しません。一方コイルが一定の速さ で 軸正の向きに時刻 だけ進むと,A の座標は となります。したがって, は に対して単調に減少することがわかります。
(2) ニ・ホ
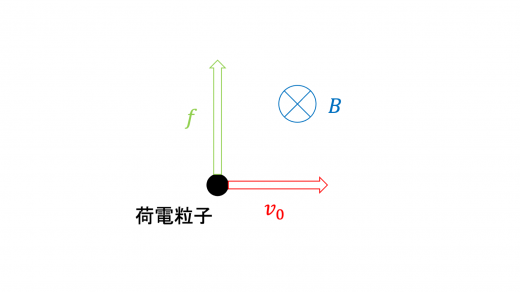
では,速さ で運動する荷電粒子にはたらくローレンツ力 (ローレンツ力の意味と式|磁場中の荷電粒子の運動) の大きさは となり,力の向きは上図のようになります。この等速円運動の半径を とすると,等速円運動の運動方程式 (円運動とは|円運動における加速度・向心力・遠心力) より
となります。
この等速円運動の角振動数 は, より
ではじめて に到達するまでにかかる時間 は,角振動数 の1周期の半分に等しく
となります。
問1
B とします。 から での荷電粒子の運動を考えます。 では,荷電粒子にはローレンツ力 がはたらきます。この等速円運動の半径 は,運動方程式より
角振動数 は
再び に達するまでの時間 は
での軌道と での軌道とは滑らかにつながることより, での等速円運動の始点は時刻 での荷電粒子の位置であるとしてよく,時刻 から までの運動の軌道は下図のようになります。
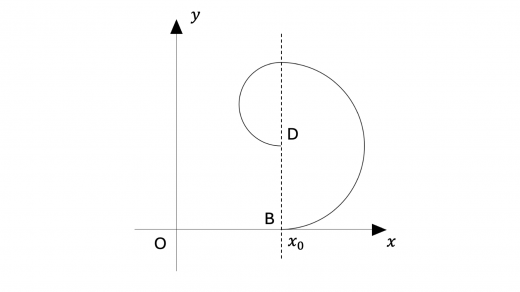
上図より時刻 での荷電粒子の位置を D とすると, がベクトル の大きさに等しく
と求められます。
(2) ヘ・ト
のとき,運動の周期 は,ホおよび問1の結果より
と求められます (ヘ:)。
また, は
問題文よりドリフトの平均の速さ は,
と求められます (ト;)。
問2
で1,2回目に に到達する時刻をそれぞれ とします。
まず, から までの運動を考えます。ローレンツ力により,この運動の軌道は下図黒実線のような円弧になります。
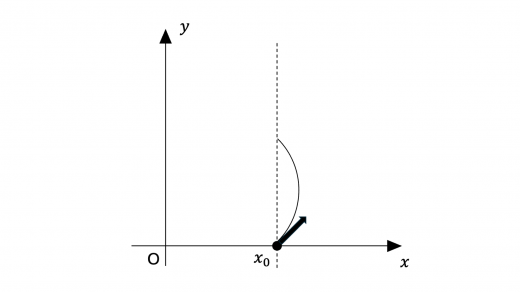
したがって,解答は①,③,⑤,⑥のいずれかとなります。
次に, から までの運動の軌道も,問1と同様に考えることができます。 での荷電粒子の速度およびローレンツ力の向きより,軌道は①か③となります。
いま, での円運動の軌道 は,それぞれ
と表されます。 より であることから,軌道は ③ であることがわかります。
(3)
外力が保存力であることより,力学的エネルギー保存則 (力学的エネルギー保存則の導出と例題) が成り立ちます。外力の向きより, 座標が等しい位置では荷電粒子の速さは等しくなると考えられるので,荷電粒子の 座標が最小値 にあるときから再び の位置に戻ってきたとき,粒子の速さは で変わらない (チ:③) であることがわかります。
での荷電粒子の等速円運動の半径 を求めます。外力 はローレンツ力に比べて十分小さいとき,運動方程式においては外力 は無視できて,
この等速円運動の角振動数 は
となります。
でも荷電粒子は同様に等速円運動を行います。 での議論から,半径 および角振動数 は,それぞれ
であるとわかります。
したがって,時刻 で2回目に に達するまでの時刻 は
となります (ヌ:)。
より であるから,この1周期の運動の軌道は問1と同様になるので,ドリフトのベクトルの向きは 軸正の向きであることがわかり (ル:②),そのベクトルの大きさ は
このドリフトの平均の速さ は
となります (ヲ:)。
問題文より, と の違いによる運動エネルギーの差が外力による仕事 に等しいと考えることができます。ここで は
であるので,
したがってドリフトの平均の速さ は, を用いて
と表すことができます。
問3
をワの結果に代入して,求めるドリフトの平均の速さ は
と求められます。 は粒子が帯びる電荷量に依存しないことに注意してください。
で1・2回目に に到達する時刻をそれぞれ とします。
での等速円運動の半径は,それぞれ上の で与えられます。
一方,電荷が となった場合の での等速円運動の半径および周期を および とすると,
が成り立ちます。 は電荷によらないので,電荷が の場合の2周期分のドリフトの距離と,電荷が の場合の1周期分のドリフトの距離は変わらないことに注意すると,求める答えは下図のような軌道になります。
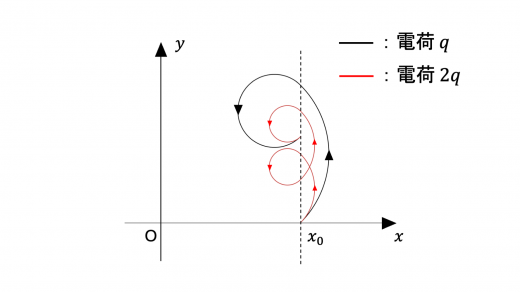
(3)の設定が少し特殊です。しっかり問題を読み,どのような条件で考えるべきか正しく読み取ることが大切です。











