(1) ア〜オ
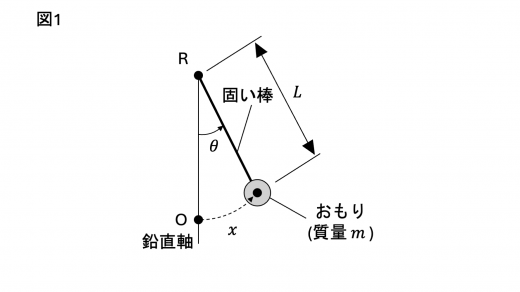
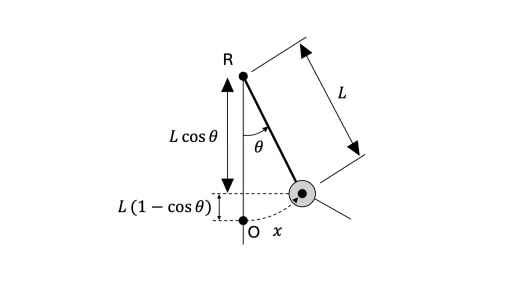
振り子の変位 x x x θ \theta θ
x = L θ
x = L \theta
x = L θ
という関係があります。
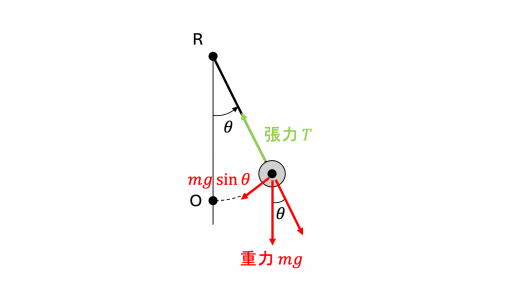
振り子の円周方向の運動方程式を考えるために,振り子にはたらく力について考えます。
このように,振り子にはたらく力のうち,円周方向に寄与するのは,重力の円周方向の成分のみです。この成分は向きまで含めて − m g sin θ - mg \sin{\theta} − m g sin θ ∣ θ ∣ |\theta| ∣ θ ∣ sin θ ∼ θ \sin{\theta} \sim \theta sin θ ∼ θ a a a
m a = − m g θ = − m g L x
ma = - mg \theta = - \dfrac{mg}{L}x
ma = − m g θ = − L m g x
となります (ア :− m g L - \dfrac{mg}{L} − L m g
これより振り子は単振動 (単振動のまとめ ) し,その角振動数は イ :g L \sqrt{\dfrac{g}{L}} L g
振動中のある時刻でのおもりの円周方向の速度 v = v 0 v = v_0 v = v 0 x = x 0 x = x_0 x = x 0 運動量保存則とエネルギー保存則の導出 ) を考えます。このときの棒の回転角を θ 0 \theta_0 θ 0 x 0 = L θ 0 x_0 = L \theta_0 x 0 = L θ 0
運動エネルギー K K K
K = 1 2 m v 0 2
K = \dfrac{1}{2} m v_0^2
K = 2 1 m v 0 2
と求められます。
x = 0 x = 0 x = 0 U U U
上図より,回転角が θ 0 \theta_0 θ 0 U U U
U = m g ( L − L cos θ 0 ) = m g L ( 1 − cos θ 0 ) = 1 2 m g L θ 0 2 = 1 2 m g L x 0 2
\begin{aligned}
U &= m g (L - L \cos{\theta_0}) \\
&= mgL (1 -\cos{\theta_0}) \\
&= \dfrac{1}{2} mg L \theta_0^2 = \dfrac{1}{2} \dfrac{mg}{L} x_0^2
\end{aligned}
U = m g ( L − L cos θ 0 ) = m gL ( 1 − cos θ 0 ) = 2 1 m gL θ 0 2 = 2 1 L m g x 0 2
したがって,x = 0 x = 0 x = 0 E E E
E = K + U = 1 2 m v 0 2 + 1 2 m g L x 0 2 (ウ)
\begin{aligned}
E &= K + U \\
&= \dfrac{1}{2} m v_0^2 + \dfrac{1}{2} \dfrac{mg}{L} x_0^2 \tag{ウ}
\end{aligned}
E = K + U = 2 1 m v 0 2 + 2 1 L m g x 0 2 ( ウ )
となります。
x = 0 x = 0 x = 0 V V V
1 2 m V 2 = 1 2 m v 0 2 + 1 2 m g L x 0 2
\dfrac{1}{2} m V^2 = \dfrac{1}{2} m v_0^2 + \dfrac{1}{2} \dfrac{mg}{L} x_0^2
2 1 m V 2 = 2 1 m v 0 2 + 2 1 L m g x 0 2
∴ V = v 0 2 + x 0 2 L (エ)
\therefore V = \sqrt{v_0^2 + \dfrac{x_0^2}{L}} \tag{エ}
∴ V = v 0 2 + L x 0 2 ( エ )
とわかります。
また,この単振動における振幅 l l l v = 0 v =0 v = 0
1 2 m g L l 2 = 1 2 m v 0 2 + 1 2 m g L x 0 2
\dfrac{1}{2} \dfrac{mg}{L} l^2 = \dfrac{1}{2} m v_0^2 + \dfrac{1}{2} \dfrac{mg}{L} x_0^2
2 1 L m g l 2 = 2 1 m v 0 2 + 2 1 L m g x 0 2
∴ l = L g v 0 2 + x 0 2 (オ)
\therefore l = \sqrt{\dfrac{L}{g} v_0^2 + x_0^2} \tag{オ}
∴ l = g L v 0 2 + x 0 2 ( オ )
と求められます。
問1
t > 0 t > 0 t > 0 t 1 , t 2 , t 3 t_1, t_2, t_3 t 1 , t 2 , t 3
2つのおもりは質量が等しく,反発係数が 1 であることより,これらのおもりが衝突すると,互いの速度を交換することがわかります (弾性衝突(完全弾性衝突)の定義と性質 )。
したがって,t = 0 t = 0 t = 0 − v 1 , 0 -v_1, 0 − v 1 , 0
t > 0 t > 0 t > 0
A の単振動の振幅と周期を求めます。まず,角振動数を求めましょう。
上図のように,A が正の方向に運動しているとき,問題文よりばねは x x x
m a = − m g L x − k x = − ( m g L + k ) x
ma = - \dfrac{mg}{L} x - kx = - \left( \dfrac{mg}{L} + k \right) x
ma = − L m g x − k x = − ( L m g + k ) x
したがって,この単振動の角振動数 ω A \omega_A ω A
ω A = g L + k m = g L + 3 g L = 2 g L
\begin{aligned}
\omega_A &= \sqrt{\dfrac{g}{L} + \dfrac{k}{m}} \\
&= \sqrt{\dfrac{g}{L} + \dfrac{3g}{L}} \\
&= 2 \sqrt{\dfrac{g}{L}}
\end{aligned}
ω A = L g + m k = L g + L 3 g = 2 L g
t > 0 t > 0 t > 0 t 1 t_1 t 1
t 1 = π ω A = π 2 L g
t_1 = \dfrac{\pi}{\omega_A} = \dfrac{\pi}{2} \sqrt{\dfrac{L}{g}}
t 1 = ω A π = 2 π g L
となります。
A の単振動の振幅 l A l_A l A x = − l A x = - l_A x = − l A l A l_A l A x = 0 x =0 x = 0
1 2 m g L l A 2 + 1 2 k l A 2 = 2 m g L l A 2 = 1 2 m v 1 2
\dfrac{1}{2} \dfrac{mg}{L} l_A^2 + \dfrac{1}{2} k l_A^2 = 2 \dfrac{mg}{L} l_A^2 = \dfrac{1}{2} m v_1^2
2 1 L m g l A 2 + 2 1 k l A 2 = 2 L m g l A 2 = 2 1 m v 1 2
∴ l A = 1 2 L g v 1
\therefore l_A = \dfrac{1}{2} \sqrt{\dfrac{L}{g}} v_1
∴ l A = 2 1 g L v 1
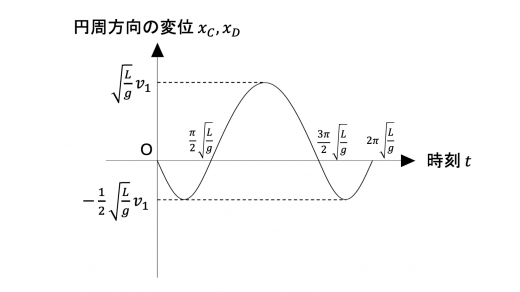
t = t 1 t = t_1 t = t 1 v 1 v_1 v 1 0 , v 1 0, v_1 0 , v 1
t 1 < t < t 2 t_1 < t < t_2 t 1 < t < t 2 ω B = g L ( = 1 2 ω A ) \omega_B = \sqrt{\dfrac{g}{L}} \left( = \dfrac{1}{2} \omega_A \right) ω B = L g ( = 2 1 ω A )
t 2 − t 1 = π ω B = π L g = 2 t 1
\begin{aligned}
t_2 - t_1 &= \dfrac{\pi}{\omega_B} \\
&= \pi \sqrt{\dfrac{L}{g}} = 2 t_1
\end{aligned}
t 2 − t 1 = ω B π = π g L = 2 t 1
となります。
また,この単振動の振幅 l B l_B l B ウ を用いたエネルギー保存則より
l B = L g v 1 ( = 2 l A )
l_B = \sqrt{\dfrac{L}{g}} v_1 ( = 2 l_A)
l B = g L v 1 ( = 2 l A )
と求められます。
t = t 2 t = t_2 t = t 2 0 , − v 1 0, -v_1 0 , − v 1 t = 0 t = 0 t = 0
したがって,t 2 < t < t 3 t_2 < t < t_3 t 2 < t < t 3 x A , x B x_A, x_B x A , x B 0 < t < t 1 0 < t < t_1 0 < t < t 1
これより x A , x B x_A, x_B x A , x B 0 ≤ t ≤ t 3 0 \leq t \leq t_3 0 ≤ t ≤ t 3
(1) カ〜ク
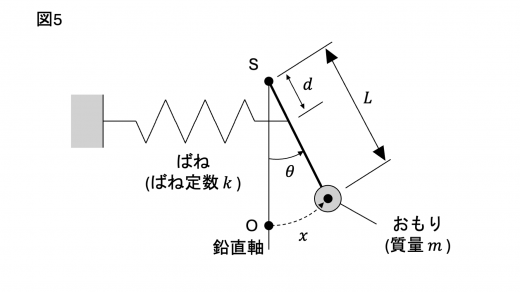
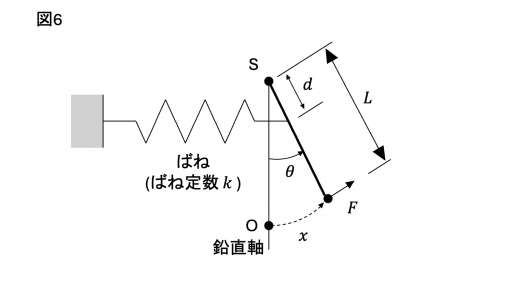
問題文より,ばねの伸び s s s d d d θ \theta θ x = L θ x = L \theta x = L θ
s = d θ = d L x (カ)
\begin{aligned}
s &= d \theta \\
&= \dfrac{d}{L} x \tag{カ}
\end{aligned}
s = d θ = L d x ( カ )
と表すことができます。
振り子の運動中におもりと棒の間にはたらく力について考えます。そのために,おもりから棒にはたらく力 (の円周方向成分) について考えてみます。棒の質量が無視できること,ばねが十分長いこと,棒にはたらく力の点 S まわりのモーメントのつりあい (力のモーメントと角運動量の関係 ) が成り立っていることより
k s ⋅ d = F ⋅ L
ks \cdot d = F \cdot L
k s ⋅ d = F ⋅ L
∴ F = k s d L = ( d L ) 2 k x (キ)
\begin{aligned}
\therefore F &= ks \dfrac{d}{L} \\
&= \left( \dfrac{d}{L} \right)^2 kx \tag{キ}
\end{aligned}
∴ F = k s L d = ( L d ) 2 k x ( キ )
と求められます。
作用・反作用の法則 (作用反作用の法則〜ニュートンの第3法則〜 ) より,棒からおもりへは逆向きの力がはたらきます。したがって,おもりの円周方向の運動方程式は
m a = − m g L x − F = − [ m g L + ( d L ) 2 k ] x
ma = - \dfrac{mg}{L} x - F = - \left[ \dfrac{mg}{L} + \left( \dfrac{d}{L} \right)^2 k \right] x
ma = − L m g x − F = − [ L m g + ( L d ) 2 k ] x
この単振動の角振動数 ω F \omega_F ω F
ω F = g L + ( d L ) 2 k m (ク)
\omega_F = \sqrt{\dfrac{g}{L} + \left( \dfrac{d}{L} \right)^2 \dfrac{k}{m}} \tag{ク}
ω F = L g + ( L d ) 2 m k ( ク )
のように求められます。
(2)
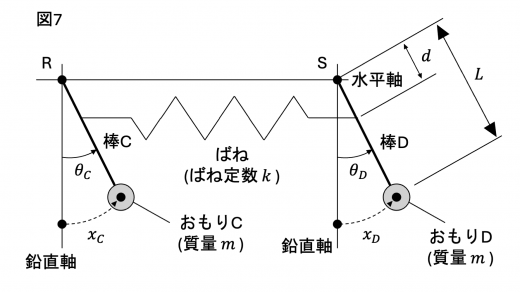
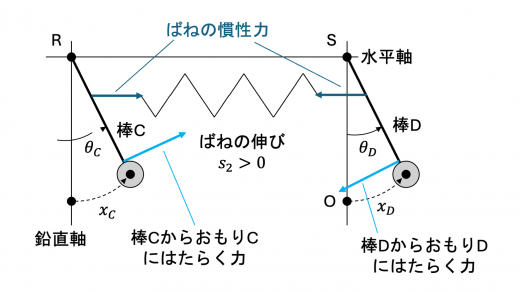
図7 の設定で考えます。
おもり C,D の変位がそれぞれ x C , x D x_C, x_D x C , x D s 2 s_2 s 2 カ と同様に考えて
s 2 = d θ D − d θ C = d L ( x D − x C ) (ケ)
s_2 = d \theta_D - d \theta_C = \dfrac{d}{L} (x_D - x_C) \tag{ケ}
s 2 = d θ D − d θ C = L d ( x D − x C ) ( ケ )
と表されます。
簡単のため s 2 > 0 s_2 > 0 s 2 > 0 図6 と同じ向き,棒 C がおもり C におよぼす力は図6 と逆向きであることがわかります。したがって,おもり C,D の円周方向の運動方程式は
{ m a C = − m g L x C + ( d L ) 2 k ( x D − x C ) m a D = − m g L x D − ( d L ) 2 k ( x D − x C )
\begin{equation}
\left \{
\begin{aligned}
& m a_C = - \dfrac{mg}{L} x_C + \left( \dfrac{d}{L} \right)^2 k (x_D - x_C) \\
& m a_D = - \dfrac{mg}{L} x_D - \left( \dfrac{d}{L} \right)^2 k (x_D - x_C)
\end{aligned}
\right.
\end{equation}
⎩ ⎨ ⎧ m a C = − L m g x C + ( L d ) 2 k ( x D − x C ) m a D = − L m g x D − ( L d ) 2 k ( x D − x C )
と書くことができます
(コ :− m g L x C + ( d L ) 2 k ( x D − x C ) - \dfrac{mg}{L} x_C + \left( \dfrac{d}{L} \right)^2 k (x_D - x_C) − L m g x C + ( L d ) 2 k ( x D − x C ) サ :− m g L x D − ( d L ) 2 k ( x D − x C ) - \dfrac{mg}{L} x_D - \left( \dfrac{d}{L} \right)^2 k (x_D - x_C) − L m g x D − ( L d ) 2 k ( x D − x C )
ここで,2つの振り子が同じ振動数 ω \omega ω a C = − ω 2 x C , a D = − ω 2 x D a_C = - \omega^2 x_C, a_D = - \omega^2 x_D a C = − ω 2 x C , a D = − ω 2 x D
{ ①: a C = − ω 2 x C = − g L x C + ( d L ) 2 k m ( x D − x C ) ②: a D = − ω 2 x D = − g L x D − ( d L ) 2 k m ( x D − x C )
\begin{equation}
\left \{
\begin{aligned}
& ①:a_C = - \omega^2 x_C = - \dfrac{g}{L} x_C + \left( \dfrac{d}{L} \right)^2 \dfrac{k}{m} (x_D - x_C) \\
& ②:a_D = - \omega^2 x_D = - \dfrac{g}{L} x_D - \left( \dfrac{d}{L} \right)^2 \dfrac{k}{m} (x_D - x_C)
\end{aligned}
\right.
\end{equation}
⎩ ⎨ ⎧ ① : a C = − ω 2 x C = − L g x C + ( L d ) 2 m k ( x D − x C ) ② : a D = − ω 2 x D = − L g x D − ( L d ) 2 m k ( x D − x C )
①+② より
− ω 2 ( x C + x D ) = − g L ( x C + x D )
-\omega^2 (x_C + x_D) = - \dfrac{g}{L} (x_C + x_D)
− ω 2 ( x C + x D ) = − L g ( x C + x D )
X 1 = x C + x D 2 X_1 = \dfrac{x_C + x_D}{2} X 1 = 2 x C + x D
( ω 2 − g L ) X 1 = 0
\left( \omega^2 - \dfrac{g}{L} \right) X_1 = 0
( ω 2 − L g ) X 1 = 0
∴ ③: ω = g L or ④: X 1 = 0 ( ∀ t )
\therefore ③:\omega = \sqrt{\dfrac{g}{L}} \, \text{or} \, ④:X_1 = 0 \, (\forall t)
∴ ③ : ω = L g or ④ : X 1 = 0 ( ∀ t )
一方 ①-② より
− ω 2 ( x C − x D ) = − g L ( x C − x D ) − 2 ( d L ) 2 k m ( x C − x D ) = − [ g L + 2 ( d L ) 2 k m ] ( x C − x D )
\begin{aligned}
-\omega^2 (x_C - x_D) &= - \dfrac{g}{L} (x_C - x_D) - 2 \left( \dfrac{d}{L} \right)^2 \dfrac{k}{m} (x_C - x_D) \\
&= - \left[ \dfrac{g}{L} + 2 \left( \dfrac{d}{L} \right)^2 \dfrac{k}{m} \right] (x_C - x_D)
\end{aligned}
− ω 2 ( x C − x D ) = − L g ( x C − x D ) − 2 ( L d ) 2 m k ( x C − x D ) = − [ L g + 2 ( L d ) 2 m k ] ( x C − x D )
X 2 = x C − x D 2 X_2 = \dfrac{x_C - x_D}{2} X 2 = 2 x C − x D
( ω 2 − [ g L + 2 ( d L ) 2 k m ] ) X 2 = 0
\left( \omega^2 - \left[ \dfrac{g}{L} + 2 \left( \dfrac{d}{L} \right)^2 \dfrac{k}{m} \right] \right) X_2 = 0
( ω 2 − [ L g + 2 ( L d ) 2 m k ] ) X 2 = 0
∴ ⑤: ω = g L + 2 ( d L ) 2 k m or ⑥: X 2 = 0 ( ∀ t )
\therefore ⑤:\omega = \sqrt{\dfrac{g}{L} + 2 \left( \dfrac{d}{L} \right)^2 \dfrac{k}{m}} \, \text{or} \, ⑥:X_2 = 0 \, (\forall t)
∴ ⑤ : ω = L g + 2 ( L d ) 2 m k or ⑥ : X 2 = 0 ( ∀ t )
(補足) 解の同値変形
連立方程式の同値変形により
( ① and ② ) ⇔ ( ③ or ④ ) and ( ⑤ or ⑥ )
(① \, \text{and} \, ②) \Leftrightarrow (③ \, \text{or} \, ④) \text{and} (⑤ \, \text{or} \, ⑥)
( ① and ② ) ⇔ ( ③ or ④ ) and ( ⑤ or ⑥ )
さらに分配法則により
( ③ or ④ ) and ( ⑤ or ⑥ ) ⇔ ( ( ③ or ④ ) and⑤ ) or ( ( ③ or ④ ) and⑥ ) ⇔ ( ③ and ⑤ ) or ( ③ and ⑥ ) or ( ④ and ⑤ ) or ( ④ and ⑥ )
\begin{aligned}
(③ \, \text{or} \, ④) \text{and} (⑤ \, \text{or} \, ⑥) & \Leftrightarrow ((③ \, \text{or} \, ④) \, \text{and} ⑤) \, \text{or} \, ((③ \, \text{or} \, ④) \, \text{and} ⑥) \\
& \Leftrightarrow (③ \, \text{and} \, ⑤) \, \text{or} \, (③ \, \text{and} \, ⑥) \\
& \qquad \text{or} \, (④ \, \text{and} \, ⑤) \, \text{or} \, (④ \, \text{and} \, ⑥)
\end{aligned}
( ③ or ④ ) and ( ⑤ or ⑥ ) ⇔ (( ③ or ④ ) and ⑤ ) or (( ③ or ④ ) and ⑥ ) ⇔ ( ③ and ⑤ ) or ( ③ and ⑥ ) or ( ④ and ⑤ ) or ( ④ and ⑥ )
ここで,( ③ and ⑤ ) (③ \, \text{and} \, ⑤) ( ③ and ⑤ ) ( ④ and ⑥ ) (④ \, \text{and} \, ⑥) ( ④ and ⑥ )
( ① and ② ) ⇔ ( ③ and ⑥ ) or ( ④ and ⑤ )
(① \, \text{and} \, ②) \Leftrightarrow (③ \, \text{and} \, ⑥) \, \text{or} \, (④ \, \text{and} \, ⑤)
( ① and ② ) ⇔ ( ③ and ⑥ ) or ( ④ and ⑤ )
が成り立ちます。
したがって,ω \omega ω
ω 1 = g L , ω 2 = g L + 2 ( d L ) 2 k m
\omega_1 = \sqrt{\dfrac{g}{L}}, \omega_2 = \sqrt{\dfrac{g}{L} + 2 \left( \dfrac{d}{L} \right)^2 \dfrac{k}{m}}
ω 1 = L g , ω 2 = L g + 2 ( L d ) 2 m k
が得られます (シ :g L + 2 ( d L ) 2 k m \sqrt{\dfrac{g}{L} + 2 \left( \dfrac{d}{L} \right)^2 \dfrac{k}{m}} L g + 2 ( L d ) 2 m k
ω = ω 1 \omega = \omega_1 ω = ω 1 x C = x D x_C = x_D x C = x D ス :1)。
一方 ω = ω 2 \omega = \omega_2 ω = ω 2 x C = − x D x_C = - x_D x C = − x D セ :-1)。
問2
ω = ω 1 \omega = \omega_1 ω = ω 1
x C = x D = a 1 sin ( ω 1 t + ϕ 1 )
x_C = x_D = a_1 \sin{(\omega_1 t + \phi_1)}
x C = x D = a 1 sin ( ω 1 t + ϕ 1 )
一方,ω = ω 2 \omega = \omega_2 ω = ω 2
x C = − x D = a 2 sin ( ω 2 t + ϕ 2 )
x_C = - x_D = a_2 \sin{(\omega_2 t + \phi_2)}
x C = − x D = a 2 sin ( ω 2 t + ϕ 2 )
と表すことができます。問題文より,一般には変位 x C , x D x_C, x_D x C , x D
x C = A 1 sin ( ω 1 t + ϕ 1 ) + A 2 sin ( ω 2 t + ϕ 2 )
x_C = A_1 \sin{(\omega_1 t + \phi_1)} + A_2 \sin{(\omega_2 t + \phi_2)}
x C = A 1 sin ( ω 1 t + ϕ 1 ) + A 2 sin ( ω 2 t + ϕ 2 )
x D = B 1 sin ( ω 1 t + ϕ 1 ) − B 2 sin ( ω 2 t + ϕ 2 )
x_D = B_1 \sin{(\omega_1 t + \phi_1)} - B_2 \sin{(\omega_2 t + \phi_2)}
x D = B 1 sin ( ω 1 t + ϕ 1 ) − B 2 sin ( ω 2 t + ϕ 2 )
一方ばねの伸びは x D − x C x_D - x_C x D − x C 2 ω 1 2 \omega_1 2 ω 1
ω 2 = 2 ω 1
\omega_2 = 2 \omega_1
ω 2 = 2 ω 1
ω 2 2 = 4 ω 1 2
\omega_2^2 = 4 \omega_1^2
ω 2 2 = 4 ω 1 2
が成り立ちます。
上述した解を代入して
g L + 2 ( d L ) 2 k m = 4 g L
\dfrac{g}{L} + 2 \left( \dfrac{d}{L} \right)^2 \dfrac{k}{m} = 4 \dfrac{g}{L}
L g + 2 ( L d ) 2 m k = 4 L g
k = 6 m g L k = \dfrac{6mg}{L} k = L 6 m g
g L + 2 ( d L ) 2 6 g L = 4 g L
\dfrac{g}{L} + 2 \left( \dfrac{d}{L} \right)^2 \dfrac{6g}{L} = 4 \dfrac{g}{L}
L g + 2 ( L d ) 2 L 6 g = 4 L g
∴ d L = 1 2
\therefore \dfrac{d}{L} = \dfrac{1}{2}
∴ L d = 2 1
と求めることができます。
問題に丁寧にしたがっていけば,方針は立てやすい問題です。この問題のような近似の使い方は一度触れておきたいです。