弾性衝突(完全弾性衝突)の定義と性質
この記事では,弾性衝突について解説します。まず,弾性衝突の定義をしっかりと押さえた後,例題を通して,弾性衝突の重要な性質を学びます。
この記事に関連するQ&A
弾性衝突(完全弾性衝突)の定義
弾性衝突(完全弾性衝突)の定義
まず,弾性衝突を定義するために,反発係数の定義を以下で説明します。
衝突面に垂直な方向の相対速度の大きさが,反応前後で衝突により, 倍になっている時,この を反発係数という。一般に反応前後で相対速度の向きは反転する。
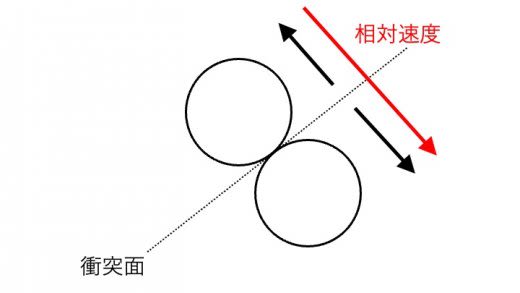
反発係数は,一般に です。( となると,2つの物体の運動エネルギーの和が,急に衝突により増えることになり,力学的エネルギー保存に反します。)以上のことを踏まえて,以下で弾性衝突の定義を紹介します。
を満たす衝突のことを,弾性衝突(完全弾性衝突)という。
ちなみに, を満たす衝突のことを,非弾性衝突と言います。以下で例題を通して,弾性衝突の際に成り立つ重要な性質について見ていきましょう。
例題〜等質量物体の弾性衝突〜
例題〜等質量物体の弾性衝突〜
1次元を動く質点1が,速度 で,静止していた質点2に弾性衝突した。衝突後の質点1,2の速度, をそれぞれ求めよ。ただし,質点1,2の質量は互いに等しいとする。


質点1,2の質量を とする。
この衝突は弾性衝突なので, また,系全体の運動量は保存するので, 2式を解いて, を得る。
衝突前の質点1,2の速度と,衝突後の速度を比較してみると,速度が「交換」していることがわかります。一般に次の公式が成り立ちます。
等質量物体同士の弾性衝突では,速度が交換する。
運動量保存の法則と,反発係数の定義式の2式を連立させる,衝突前後の速度の求め方は,大学入試でも頻出なので,確実に押さえましょう。
例題〜エネルギー保存〜
例題〜エネルギー保存〜
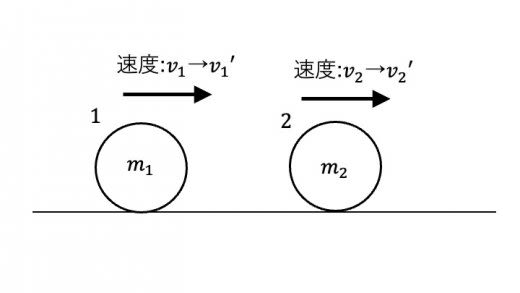
質点同士の弾性衝突において,衝突前後で運動エネルギーが保存することを示せ。
質量がそれぞれ , の質点 , が弾性衝突するとする。衝突前の速度は質点1,2でそれぞれ,,衝突後の速度はそれぞれ, であったとする。
運動量保存と弾性衝突の関係式より,以下が成り立つ。
これらを解いて,
を得る。この結果を用いると,
となり,運動エネルギーは保存する。
一般に衝突の前後では,運動エネルギーは保存しませんが,弾性衝突の時のみ,保存することがわかります。
ここで紹介した,弾性衝突の性質は非常に有名です。











