ホール効果

ホール効果とその仕組み

ホール効果とは，電流が流れている物体(導体，半導体など)に，電流と直交するように磁場をかけると，物体内に電位差(あるいは電場)が発生する現象のことです。

導体を例に取り，ホール効果の仕組みについて考えてみましょう。

下図のように，直方体の導体の $x$ 方向に電流 $I$ が流れているときを考えます。また，磁場 $B$ が $z$ 軸正方向に一様にはたらいているとします。

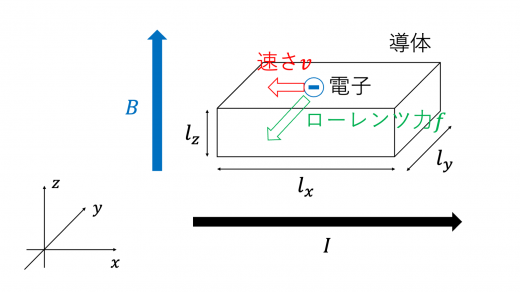
このとき，電流とは逆方向，すなわち $x$ 軸負の方向に電子が速さ $v$ で運動します。いま，電子の速度と磁場とが直交しているため，電子は磁場からローレンツ力

$$f = e v B$$

を受けます。このローレンツ力は $y$ 軸負の方向にはたらいています。(ローレンツ力の大きさと向きの求め方は ローレンツ力の意味と式｜磁場中の荷電粒子の運動 をご覧ください。)

定常状態では，下図のように，直方体の面 $Y_{+}$ と $Y_{-}$ に，それぞれ正および負の電荷が配置します。

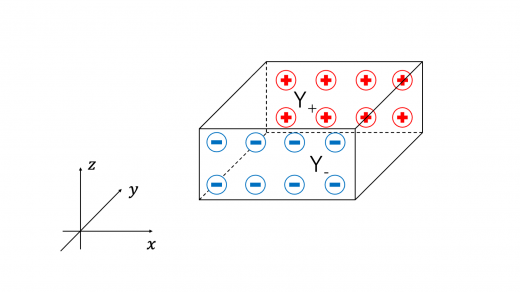
これより，導体内では $y$ 軸負の方向に電場・電圧が発生することになります。

このときの $y$ 軸方向の電位差をホール電圧と呼びます。

ホール電圧の求め方

上の議論にて，電荷分布が定常状態になったときを考えます。このとき，電子にはたらくクーロン力とローレンツ力とが等しくなっています。定常状態では電荷は導体表面にのみ分布するので，導体内の電場は一定となっています。

いま，ホール電圧を $V_H$ とします。上図より，導体内には $y$ 軸負の方向に大きさ $V_H/l_y$ の電場がはたらいています。電子にはたらく力のつりあいより

$$e \dfrac{V_H}{l_y} = e v B$$

$$\therefore V_H = v B l_y \tag{1}$$

また，電流 $I$ を用いても $V_H$ を表すことができます。電流の大きさは，電荷の速さ $v$，導体内の電荷の数密度 $n$ を用いて

$$I = v l_y l_z n e$$

と表すことができます。これを用いると

$$V_H = \dfrac{I B}{l_z n e} \tag{2}$$

とも表すことができます。

(1)・(2)式の右辺の単位が[V]になっていることは，次元解析により確かめることができるので，ぜひ確かめてみてください。

半導体にはn型とp型の2種類が存在します。ホール効果は，半導体がどちらの型なのか判別するのに用いることができます。

電流を担う粒子をキャリアと呼びます。詳しい説明はここでは割愛しますが，半導体を構成する原子をうまく選ぶことで，キャリアが負電荷(電子)/正電荷(正孔)となるように半導体を作ることができます。前者の半導体をn型半導体，後者の半導体をp型半導体と呼びます。nはnegativeの略，pはpositiveの略と考えると覚えやすいかもしれません。

さて，n型半導体に電流を流す場合は，導体の場合とキャリアが同じ(電子)ため，上の導体での議論と同様にホール効果が発生し，半導体内には $y$ 軸負の向きの電場が生じます。

ここで，p型半導体に電流を流す場合を考えます。電流と磁場の設定は上の導体の議論と同様とします。

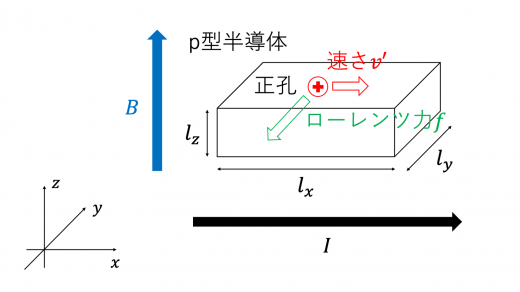
キャリアは正孔であり，これは電流と同じ $x$ 軸正方向に速さ $v'$ で運動しています。このキャリアは上図のように，$y$ 軸負の方向にローレンツ力を受けます。定常状態での電荷分布は以下のように，n型半導体の場合と逆になります。

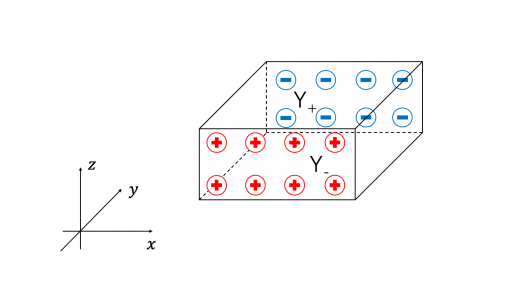
したがって，p型半導体内部には $y$ 軸正の方向に電場・電圧がはたらくことになります。これはn型半導体内部のホール電圧(電場)の向きとは逆になっています。

上の議論で見たように，同じ方向に電流と磁場を設定すると，n型とp型でホール電圧(および電場)の方向が逆となります。したがって，ホール電圧(あるいは電場)の向きを測定することで，使っている半導体がn型とp型のどちらなのかを判別することができます。