慣性力の定義と見かけの重力の例題

更新 2022/02/09

この記事では，慣性力を解説していきます。まず慣性系の定義をあたえ，主に並進運動による慣性系の扱いについて，理論と実践をバランスよく行うのが目標です。

慣性力の定義

まず，慣性力を定義していきます。慣性力を考えるためには，慣性系と非慣性系を区別して，考察していく必要があります。
慣性系において運動方程式は
ma=F
m\boldsymbol a=\boldsymbol{F}
ma=F
とかけるのでした。

では，慣性系以外の座標系での運動方程式はどうなるのでしょうか。一般に，非慣性系における運動方程式は上のような綺麗な形には欠けないことがわかります。このことから，慣性力を以下のように定義します。
慣性力の定義
非慣性系で観測したとき，一般に運動方程式に余分な項が現れる。その余分な項を左辺に移項し，力とみなしたものを慣性力と定義する。
定義だけではピンとこないので，例として，慣性系に対して加速度 a′\boldsymbol{a'}a′ で並進運動している座標系から観測する運動を考えてみましょう。この座標系を RRR とします。

RRR からみた物体が受ける力は F\boldsymbol FF となり，慣性系から見た力と変わりません。また，質量も座標系によって変わりません。(相対論的効果を考えると，F\boldsymbol FF やmmm が不変とはいえませんが，ここでは相対論的効果は無視することにします。)
一方，物体の加速度 はどうでしょうか。相対加速度の考え方を用いると，RRR からみた加速度は a−a′\boldsymbol{a}-\boldsymbol a'a−a′ とかけます。b=a−a′\boldsymbol b=\boldsymbol{a}-\boldsymbol a'b=a−a′ とおくと，a=b+a′\boldsymbol a=\boldsymbol b+\boldsymbol a'a=b+a′なので，これを上の運動方程式に代入すると，
m(b+a′)=F
m(\boldsymbol b+\boldsymbol a')=\boldsymbol F
m(b+a′)=F
となります。RRR における物体の加速度は b\boldsymbol bb だったので，
mb=F−ma′
m\boldsymbol b=\boldsymbol F-m\boldsymbol a'
mb=F−ma′
が RRR における運動方程式となります。
これを慣性系の運動方程式と比べると，左辺に余分な項，−ma-m\boldsymbol a−ma が現れています。この項のことを並進運動による慣性力と呼びます。
他にも非慣性系の運動として回転運動が考えられます。回転運動の慣性力には遠心力やコリオリ力などがあります。これらの導出は，以下の記事で詳しく解説されています。

コリオリの力の導出
この記事でも慣性系や慣性力について解説しましたが，以下の記事でもこれらについて詳しく解説されています。

慣性の法則〜ニュートンの第1法則〜

この問題の(1)番のDHを求める問題で、三角形DMAを切り出して、直線AMに垂直になるように、DHを降ろしていますが、 2

2022年慶応志木の問題です。大問▪️3の(2)番で、このような問題がありました。ここで図を書くと、添付図のようにな 3

問あなたの今の気持ちを伝える文を書こう。という問題に下記の様に答えを書きました。 ●Im glad that giv 4

エタノール（C2H5OH）の量論比での酸化反応式と理論空燃比を求めよ A) 化学反応式 B) 理論空燃比 5

慣性力の注意点

見かけの力慣性力は，本来は座標変換に起因する項なのですが，その名の通り，見かけの力としての性質を持たせます。
mb=F−ma′
m\boldsymbol b=\boldsymbol F-m\boldsymbol a'
mb=F−ma′
の左辺において，−ma′-m\boldsymbol a'−ma′ を力と同一視して，F′=F−ma′\boldsymbol F'=\boldsymbol F-m\boldsymbol a'F′=F−ma′ と置いてしまえば，上の運動方程式は
mb=F′
m\boldsymbol b=\boldsymbol F'
mb=F′
となり，慣性系における運動方程式と全く同じ形にかけるじゃないか！ということです。
このように，物理学では，物理法則がどの座標系でも同じにかけるようにしたいという強いモチベーションがあります。
慣性力を使って問題を解くここまではやや抽象的な解説をしましたが，これからは慣性力を実際に系に適用する練習をしてみます。意識すべき流れは以下です。
楽に運動方程式が書けるような加速度をもった座標系を考える。
その座標系に立っているつもりで，運動方程式を書く。
最後に，その座標系の加速度 aaa を用いて，運動方程式の左辺に −ma-m\boldsymbol a−ma を追加する。
それでは，具体的な問題を考えて計算をおこなってみましょう。

慣性力の例題1〜エレベーター〜

例題

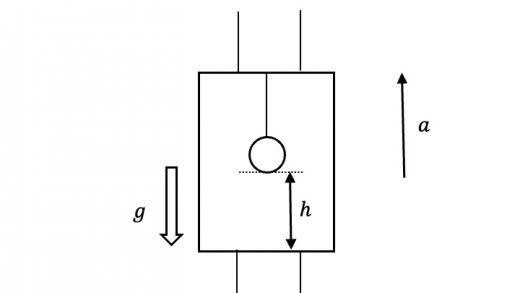エレベーターの天井から球が吊り下げられており，球の下端と床の距離は $h$ であったとする。また，エレベーターは加速度の大きさ $a$ の等加速度で上昇している。重力加速度を $g(\geq a)$ とし，球は鉛直方向にのみ運動するとする。

(1)今，突然球を吊り下げた糸が切れ，球は落下した。糸が切れた瞬間を $t=0$ とした時，球が床についた時の $t$ を求めよ。無重力

(2)エレベーターを加速度の大きさ $g$ で等加速度で下降している時，糸が切れた。エレベーターと共に運動する座標系でみた時，球はどのような運動をするか。

(1)まず「1.楽に運動方程式が書けるような加速度をもった座標系を考える。」に従ってみます。このような座標系は一般に，系の最も大きい物体と共に運動する座標系をとると，うまくいくことが多いです。この場合はエレベーターになります。

次に「2.その座標系に立っているつもりで，運動方程式を書く。」を行います。エレベーターと共に運動する座標系で，球の運動方程式は，球の質量を $m$ ，加速度を $a'$ とすると， $ma'=mg$ と書きたくなります。
しかしこの座標系は慣性系ではないので，「3. その座標系の加速度 $a$ を用いて，運動方程式の左辺に $-m\boldsymbol a$ を追加する。」を行います。すると結局，運動方程式は $ma'=m(g+a)$ とかけます。これはあたかも見かけの重力 $g+a$ がはたらいているようです。
あとは等加速度運動の公式を用いると， $h=\dfrac{1}{2}(g+a)t^2$ となるので， $t=\sqrt{\dfrac{2h}{g+a}}$ が求まります。

(2)(1)と同様に見かけの重力を考えると，見かけの重力は $g-g=0$ となることがわかります。つまりエレベーター中ではなんと局所的に無重力状態が実現していることがわかります！球は鉛直方向のみに運動するので，結局エレベーターと共に運動する座標系で見ると，球は静止することがわかります。
次の問題も，同様の見方で解いてみてください。

慣性力の例題2〜電車〜

例題

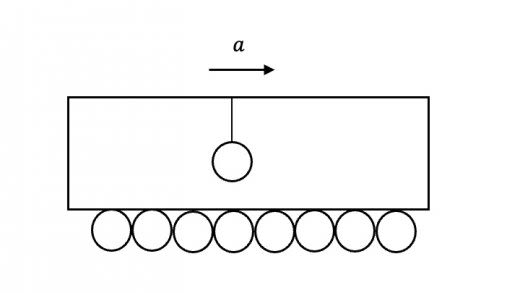電車の中で前問と同じ球を吊るした。電車が加速度 $a$ で右向きに進む時，球と糸のつりあいの状態を図示せよ。

解答

以下の図のようになる。見かけの重力とつりあい張力と見かけの重力がつり合うため，斜め方向に引っ張られる。

見かけの重力によって，物体が斜め方向に落ちていくなど，直感に反する現象が起きるのは面白いです。