• 解決済み

    @Rarara

    2023/10/29 3:00

    1 回答

    数学的センス、直感力に長けている人に聞きたいのですが、以下の領域が直感的に理解できません。

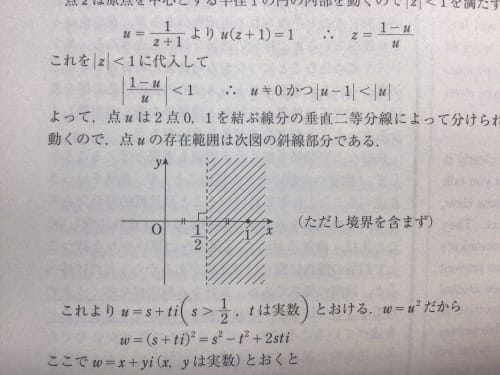
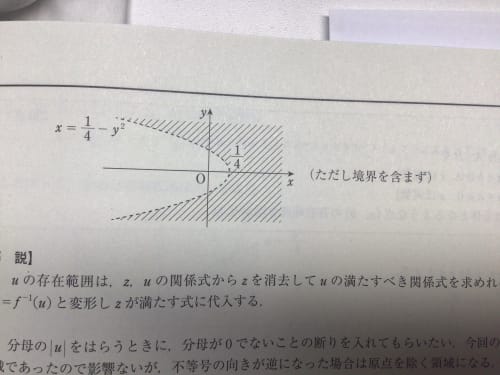
    問題は、左写真がuの存在範囲で、それに対してw=u^2の範囲を図示せよ、です。(答えは右写真)

    数式処理をした結果、私もこの結果に至りましたが、あれでもこれ間違ってないか？となってしまいました。

    理由は、uの領域の、実数部分が1/2付近で、虚数部分が無限大のuに対して、w=u^2を施すと、uの回転角はほぼ90度でwはその2倍で180度、大きさはuがでかいのでwもでかい。だから、この時のwは、x軸よりもちょっと上側で、x軸負のずっと向こう側にあると思ったのですが、この点は右写真の領域には含まれてないように見えます。なにか勘違いをしていますか？


    変な質問ですがお願いします🤲🤲


    1. 高校生
    2. 数学
    3. 数学Ⅲ

    ベストアンサー

    ベストアンサー

    @sHlcNRe46

    2023/10/30 5:02

    直感的にはたしかにそうなりますね。

    もし自分なら、以下の 33 点を考えて納得します。


    ・uu の偏角が π2\frac{\pi}{2} に近いとはいえ、π2\frac{\pi}{2} よりは小さい。つまり、w=u2w=u^2 の偏角は π\pi に近いとはいえ、π\pi よりはそこそこ小さい。

    ・uu の絶対値はかなり大きい。つまり、w=u2w=u^2 の絶対値はその 22 乗となってかなり大きい。


    まず、以上の 22 点から xx 軸との距離はかなり大きい、という事実に納得します。


    そして、

    ・放物線 x=14−y2x=\dfrac{1}{4}-y^2 は xx が十分に小さくなると傾きは 00 に近づく。


    以上の点から、いま考えている uu に対して変換した w=u2w=u^2 は、放物線より上に存在しそうだ、という事実に納得します。



    これらはすべてイメージの話なので、これに加えてやはり数式の処理にミスがないかを確認し、出てきた数式に納得するのがよいと思います。

    質問者からのお礼コメント

    質問者からのお礼コメント

    納得しました。x軸から少し上、といってもそれがずっと左に行けばいずれは無限大にだってなりえる、ということですね。無限大はもっと慎重に考えることにします。ありがとうございました。

    そのほかの回答（0件）

    関連する質問

    もっとみる