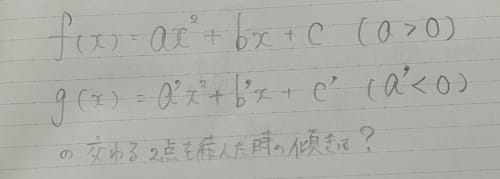答えできるだけ早くお願いいたします

この問題は数学Ⅰ・Aのみの知識で解いています。もしその先を習っているなら解きやすいように工夫してもらって構いません。

文字が多くて煩雑になりますが、解法はいたって簡単です。交点が重要なので$f(x)=g(x)$を求めてあげれば何とかなります。

$$f(x)-g(x)=(a-a')x^2+(b-b')x+c-c'=0$$

ここで、出てくる2解をA,Bとかにします。求めたいのは傾きなので、

$$(2点間の傾き)=\dfrac{f(A)-f(B)}{A-B}　こうなりますよね、もう少し分解して$$

$$\dfrac{a(A^2-B^2)+b(A-B)}{A-B}=a(A+B)+b$$

あとは少し代入するだけなので面倒ですが解を出します。

$$x=\dfrac{-(b-b')±\sqrt{(b-b')^2-4(a-a')(c-c')}}{2(a-a')}$$

これからわかる通り、$A+B=-\dfrac{b-b'}{a-a'}$なので答えは、

$$∴　\dfrac{ab'-a'b}{a-a'}$$

意外な結果になったと思います。$c,c'$がどうでもいいということになりますね

誤植などあれば教えてください