問1
問 1 は入射波と反射波の合成の問題です。
(1)
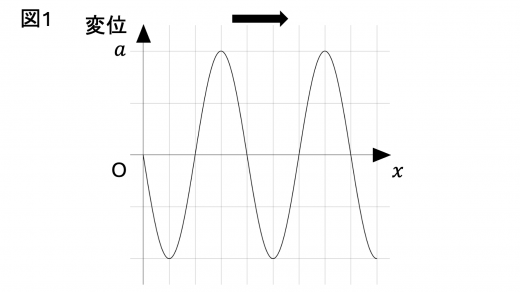
時刻 t t t x x x f i n ( t , x ) f_{in} (t, x) f in ( t , x )
x = 0 x = 0 x = 0
上図の黒線は t = 0 t =0 t = 0 t t t x = 0 x = 0 x = 0 t = 0 t = 0 t = 0 f i n ( t , 0 ) f_{in} (t, 0) f in ( t , 0 ) sin \sin sin a a a T T T ω \omega ω 正弦波の意味,特徴と基本公式 )
ω = 2 π T
\omega = \dfrac{2 \pi}{T}
ω = T 2 π
したがって,x = 0 x = 0 x = 0
f i n ( t , 0 ) = a sin ( ω t ) = a sin ( 2 π t T )
f_{in} (t, 0) = a \sin{(\omega t)}
= a \sin{\left(2 \pi \dfrac{t}{T} \right)}
f in ( t , 0 ) = a sin ( ω t ) = a sin ( 2 π T t )
と表されます。
(2)
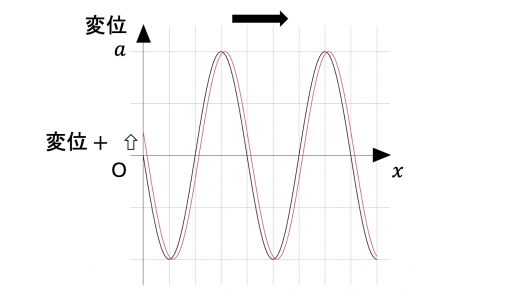
原点での変位が位置 x x x t 0 t_0 t 0 T T T λ \lambda λ v v v
v = λ T
v = \dfrac{\lambda}{T}
v = T λ
ゆえに求める時間 t 0 t_0 t 0
t 0 = x v = x λ T
t_0 = \dfrac{x}{v} = \dfrac{x}{\lambda} T
t 0 = v x = λ x T
となります。
(3)
(1)・(2) より,時刻 t t t x x x f i n ( t , x ) f_{in} (t, x) f in ( t , x )
f i n ( t , x ) = f i n ( t − t 0 , 0 ) = a sin { 2 π ( t T − x λ ) }
\begin{aligned}
f_{in} (t, x) &= f_{in} (t - t_0, 0) \\
&= a \sin{\left\{2 \pi \left( \dfrac{t}{T} - \dfrac{x}{\lambda} \right) \right\}}
\end{aligned}
f in ( t , x ) = f in ( t − t 0 , 0 ) = a sin { 2 π ( T t − λ x ) }
と表すことができます。
(あ)
固定端反射では,反射波の位相は入射波と比べて (ウ) π \pi π 入射波と反射波(固定端反射・自由端反射) )。
一方,自由端反射では,反射波の位相と入射波の位相にずれはありません。
(4)
図 2 より OH = 7 4 λ \text{OH} = \dfrac{7}{4} \lambda OH = 4 7 λ t 0 ′ t_0' t 0 ′
t 0 ′ = OH − OX v = 7 4 λ − x λ T = ( 7 4 − x λ ) T
t_0' =\dfrac{\text{OH} - \text{OX}}{v} = \dfrac{\dfrac{7}{4} \lambda - x}{\lambda} T = \left( \dfrac{7}{4} - \dfrac{x}{\lambda} \right) T
t 0 ′ = v OH − OX = λ 4 7 λ − x T = ( 4 7 − λ x ) T
と求められます。
(5)
時刻 t t t x x x f r e ( t , x ) f_{re} (t, x) f re ( t , x )
まず,時刻 t t t x = x H = 7 4 λ x = x_H = \dfrac{7}{4} \lambda x = x H = 4 7 λ f r e ( t , x H ) f_{re} (t, x_H) f re ( t , x H )
まず,時刻 t t t x H x_H x H
f i n ( t , x H ) = a sin { 2 π ( t T − 7 4 ) } = a sin ( 2 π t T − 7 2 π ) = a sin ( 2 π t T + π 2 ) = a cos ( 2 π t T )
\begin{aligned}
f_{in} (t, x_H) &= a \sin{\left\{2 \pi \left( \dfrac{t}{T} - \dfrac{7}{4} \right) \right\}} \\
&= a \sin{\left( 2 \pi \dfrac{t}{T} - \dfrac{7}{2} \pi \right)} \\
&= a \sin{\left( 2 \pi \dfrac{t}{T} + \dfrac{\pi}{2} \right)} \\
&= a \cos{\left( 2 \pi \dfrac{t}{T} \right)}
\end{aligned}
f in ( t , x H ) = a sin { 2 π ( T t − 4 7 ) } = a sin ( 2 π T t − 2 7 π ) = a sin ( 2 π T t + 2 π ) = a cos ( 2 π T t )
時刻 t t t x H x_H x H π \pi π
f r e ( t , x H ) = a cos ( 2 π t T + π ) = − a cos ( 2 π t T )
f_{re} (t, x_H) = a \cos{\left( 2 \pi \dfrac{t}{T} + \pi \right)} = - a \cos{\left( 2 \pi \dfrac{t}{T} \right)}
f re ( t , x H ) = a cos ( 2 π T t + π ) = − a cos ( 2 π T t )
さらに,(4) より,時刻 t t t x H x_H x H
f r e ( t , x ) = f r e ( t − t 0 ′ , x H ) = − a cos { 2 π ( t T + x λ − 7 4 ) } = − a cos { 2 π ( t T + x λ ) + π 2 } = a sin { 2 π ( t T + x λ ) }
\begin{aligned}
f_{re} (t, x) &= f_{re} (t - t_0', x_H) \\
&= - a \cos{\left\{2 \pi \left( \dfrac{t}{T} + \dfrac{x}{\lambda} - \dfrac{7}{4} \right) \right\}} \\
&= - a \cos{\left\{2 \pi \left( \dfrac{t}{T} + \dfrac{x}{\lambda} \right) + \dfrac{\pi}{2} \right\}} \\
&= a \sin{\left\{2 \pi \left( \dfrac{t}{T} + \dfrac{x}{\lambda} \right) \right\}}
\end{aligned}
f re ( t , x ) = f re ( t − t 0 ′ , x H ) = − a cos { 2 π ( T t + λ x − 4 7 ) } = − a cos { 2 π ( T t + λ x ) + 2 π } = a sin { 2 π ( T t + λ x ) }
(6)
時刻 t t t x x x g ( t , x ) g (t, x) g ( t , x )
g ( t , x ) = f i n ( t , x ) + f r e ( t , x ) = a sin { 2 π ( t T − x λ ) } + a sin { 2 π ( t T + x λ ) }
\begin{aligned}
g (t, x) &= f_{in} (t, x) + f_{re} (t, x) \\
&= a \sin{\left\{2 \pi \left( \dfrac{t}{T} - \dfrac{x}{\lambda} \right) \right\}} + a \sin{\left\{2 \pi \left( \dfrac{t}{T} + \dfrac{x}{\lambda} \right) \right\}} \\
\end{aligned}
g ( t , x ) = f in ( t , x ) + f re ( t , x ) = a sin { 2 π ( T t − λ x ) } + a sin { 2 π ( T t + λ x ) }
簡単のため 2 π t T = θ t , 2 π x λ = θ x 2 \pi \dfrac{t}{T} = \theta_t, 2 \pi \dfrac{x}{\lambda} = \theta_x 2 π T t = θ t , 2 π λ x = θ x
g ( t , x ) = a sin ( θ t + θ x ) + a sin ( θ t − θ x ) = 2 a sin θ t cos θ x
\begin{aligned}
g (t, x) &= a \sin{(\theta_t + \theta_x)} + a \sin{(\theta_t - \theta_x)} \\
&= 2 a \sin{\theta_t} \cos{\theta_x}
\end{aligned}
g ( t , x ) = a sin ( θ t + θ x ) + a sin ( θ t − θ x ) = 2 a sin θ t cos θ x
ゆえに,合成波の振幅の最大値は 2 a 2a 2 a
(い)
合成波の振幅が時刻 t t t 0 0 0
cos θ x = cos ( 2 π x λ ) = 0
\cos{\theta_x} = \cos{\left( 2 \pi \dfrac{x}{\lambda} \right)} = 0
cos θ x = cos ( 2 π λ x ) = 0
点 A 〜 G,すなわち 0 ≤ x λ ≤ 3 2 0 \leq \dfrac{x}{\lambda} \leq \dfrac{3}{2} 0 ≤ λ x ≤ 2 3 x x x
x λ = 1 4 , 3 4 , 5 4
\dfrac{x}{\lambda} = \dfrac{1}{4}, \dfrac{3}{4}, \dfrac{5}{4}
λ x = 4 1 , 4 3 , 4 5
点 A 〜 G で表現すると,点 B,D,F
(注)点 H も合成波の振幅が常に 0 となります。
問題文の指定では除かれているため注意してください。
問 2
問 2 は光の干渉の問題です。
(7)
屈折の法則 (反射の法則・屈折の法則 ) より,図 3 の入射角 i i i r r r
1 sin ( i ) = n sin ( r ) ∴ sin ( i ) = n sin ( r )
1 \sin{(i)} = n \sin{(r)} \quad \therefore \sin{(i)} = n \sin{(r)}
1 sin ( i ) = n sin ( r ) ∴ sin ( i ) = n sin ( r )
が成り立ちます。
(8)
薄膜の表面で反射した光と薄膜の底面で反射した光が強め合う条件を考えます。
ここで,光が屈折率の異なる2つの媒質 A・B (屈折率 n a , n b n_a, n_b n a , n b
ことに注意します。
上図より,薄膜の表面で反射した光は入射波と反射波の位相が π \pi π
ここで,図 3 より,これらの光の経路差 Δ \Delta Δ λ ′ \lambda' λ ′
1 ⋅ λ = n ⋅ λ ′ ∴ λ ′ = λ n
1 \cdot \lambda = n \cdot \lambda' \quad \therefore \lambda' = \dfrac{\lambda}{n}
1 ⋅ λ = n ⋅ λ ′ ∴ λ ′ = n λ
ゆえに光が強め合う条件は,0 0 0 m m m
Δ λ ′ = n Δ λ = m + 1 2
\dfrac{\Delta}{\lambda'} = n \dfrac{\Delta}{\lambda} = m + \dfrac{1}{2}
λ ′ Δ = n λ Δ = m + 2 1
図 3 より
Δ = 2 d cos ( r ) = 2 d 1 − sin 2 ( r ) = 2 d 1 − 1 n 2 sin 2 ( i )
\begin{aligned}
\Delta &= 2d \cos{(r)} \\
&= 2d \sqrt{1 - \sin^2{(r)}} \\
&= 2d \sqrt{1 - \dfrac{1}{n^2} \sin^2{(i)}}
\end{aligned}
Δ = 2 d cos ( r ) = 2 d 1 − sin 2 ( r ) = 2 d 1 − n 2 1 sin 2 ( i )
となるので,代入・整理して
2 d λ n 2 − sin 2 ( i ) = m + 1 2
\dfrac{2d}{\lambda} \sqrt{n^2 - \sin^2{(i)}} = m + \dfrac{1}{2}
λ 2 d n 2 − sin 2 ( i ) = m + 2 1
となります。
(9)
2 つの反射光が弱め合う条件は,(8) と同様に考えることで,2つの光の経路差が整数 × 波長となるときとなります。(8)と同じように式で表現すると
2 d λ n 2 − sin 2 ( i ) = m
\dfrac{2d}{\lambda} \sqrt{n^2 - \sin^2{(i)}} = m
λ 2 d n 2 − sin 2 ( i ) = m
と表されます。
(10)
λ = 720 \lambda = 720 λ = 720 k k k
2 d 720 [ n m ] n 2 − sin 2 ( i ) = k + 1 2 (1)
\dfrac{2d}{720 [nm]} \sqrt{n^2 - \sin^2{(i)}} = k + \dfrac{1}{2} \tag{1}
720 [ nm ] 2 d n 2 − sin 2 ( i ) = k + 2 1 ( 1 )
と表されます。
波長を徐々に短くして λ = 540 \lambda = 540 λ = 540
2 d 540 [ n m ] n 2 − sin 2 ( i ) = k + 1 (2)
\dfrac{2d}{540 [nm]} \sqrt{n^2 - \sin^2{(i)}} = k + 1 \tag{2}
540 [ nm ] 2 d n 2 − sin 2 ( i ) = k + 1 ( 2 )
さらに波長を短くしていき,次に光が強め合うような光の波長を λ 1 \lambda_1 λ 1 k k k
2 d λ 1 [ n m ] n 2 − sin 2 ( i ) = k + 3 2 (3)
\dfrac{2d}{\lambda_1 [nm]} \sqrt{n^2 - \sin^2{(i)}} = k + \dfrac{3}{2} \tag{3}
λ 1 [ nm ] 2 d n 2 − sin 2 ( i ) = k + 2 3 ( 3 )
これらを n , k , λ n, k, \lambda n , k , λ
まず,λ 1 \lambda_1 λ 1
2 d 540 × 720 2 d = 720 540 = 4 3 = k + 1 k + 1 2 = 2 k + 2 2 k + 1
\dfrac{2d}{540} \times \dfrac{720}{2d} = \dfrac{720}{540} = \dfrac{4}{3} = \dfrac{k + 1}{k + \dfrac{1}{2}} = \dfrac{2k + 2}{2k + 1}
540 2 d × 2 d 720 = 540 720 = 3 4 = k + 2 1 k + 1 = 2 k + 1 2 k + 2
∴ k = 1 (4)
\therefore k = 1 \tag{4}
∴ k = 1 ( 4 )
一方 (1) 式 ÷(3) 式より
2 d 720 × λ 1 2 d = λ 1 720 = k + 3 2 k + 1 2 = 2 k + 3 2 k + 1
\dfrac{2d}{720} \times \dfrac{\lambda_1}{2d} = \dfrac{\lambda_1}{720} = \dfrac{k + \dfrac{3}{2}}{k + \dfrac{1}{2}} = \dfrac{2k + 3}{2k + 1}
720 2 d × 2 d λ 1 = 720 λ 1 = k + 2 1 k + 2 3 = 2 k + 1 2 k + 3
(4) 式を代入して
λ 1 720 = 5 3 ∴ λ 1 = 432 [ nm ]
\dfrac{\lambda_1}{720} = \dfrac{5}{3} \quad \therefore \lambda_1 = 432 [\text{nm}]
720 λ 1 = 3 5 ∴ λ 1 = 432 [ nm ]
有効数字 2 桁で求めると,4.3 × 1 0 2 4.3 \times 10^2 4.3 × 1 0 2
(11)
再び (1) 式に戻ります。問題文より d = 450 d = 450 d = 450
また,角度 i i i tan ( i ) = 13 12 \tan{(i)} = \sqrt{\dfrac{13}{12}} tan ( i ) = 12 13
sin ( i ) = 13 5
\sin{(i)} = \dfrac{\sqrt{13}}{5}
sin ( i ) = 5 13
これらを (1) 式に代入して
900 540 n 2 − ( 13 5 ) 2 = 5 4 n 2 − 12 25 = 1 + 1 2 = 3 2
\dfrac{900}{540} \sqrt{n^2 - (\dfrac{\sqrt{13}}{5})^2} = \dfrac{5}{4} \sqrt{n^2 - \dfrac{12}{25}} = 1 + \dfrac{1}{2} = \dfrac{3}{2}
540 900 n 2 − ( 5 13 ) 2 = 4 5 n 2 − 25 12 = 1 + 2 1 = 2 3
∴ n 2 − 13 25 = 4 5 × 3 2 = 6 5
\therefore \sqrt{n^2 - \dfrac{13}{25}} = \dfrac{4}{5} \times \dfrac{3}{2} = \dfrac{6}{5}
∴ n 2 − 25 13 = 5 4 × 2 3 = 5 6
n > 0 n > 0 n > 0
n = 13 25 + ( 6 5 ) 2 = 49 25 = 7 5 = 1.4
\begin{aligned}
n &= \sqrt{\dfrac{13}{25} + \left( \dfrac{6}{5} \right)^2} \\
&= \sqrt{\dfrac{49}{25}} = \dfrac{7}{5} = 1.4
\end{aligned}
n = 25 13 + ( 5 6 ) 2 = 25 49 = 5 7 = 1.4
有効数字 2 桁で求めると 1.4 1.4 1.4
焦らず丁寧に取り組めば,最後まで解き切ることのできる問題です。
波動の単元の重要知識の確認もできるため,復習にも良いです。