【解答・解説】東大物理2023 第3問 -熱力学-
2023年度の東大物理第3問を解説します。熱力学の単元です。
なお,本記事中の図は全て,2023年度東京大学入試問題物理第3問を参考に,ライターが作成したものです(一部見やすさ等のためライターが変更した部分があります)。
この記事に関連するQ&A
問題
問題
以下の問題は,2023年度東京大学入試問題物理第3問から引用しています(一部修正しています)。
ゴムひもを伸ばすと,元の長さに戻ろうとする復元力がはたらく。一方でゴム膜を伸ばして広げると,その面積を小さくしようとする力がはたらく。この力を膜張力と呼ぶ。十分小さい面積 だけゴム膜を広げるのに必要な仕事 は
で与えられる。ここで は [力/長さ] の次元を持ち,膜張力の大きさを特徴づける正の係数である。ゴム膜でできた風船を膨らませると,膜張力により風船の内圧は外気圧よりも高くなる。外気圧は で常に一定とする。重力を無視し,風船は常に球形を保ち破裂しないものとして,以下の設問に答えよ。
I
図3-1のように半径 の風船とシリンダーが接続されている。
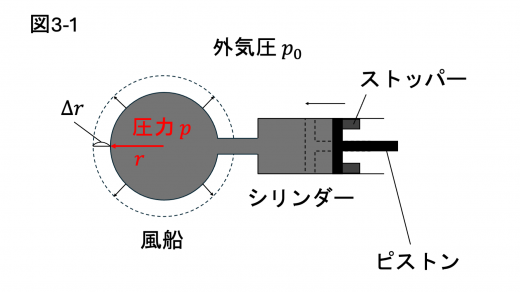
シリンダーには滑らかに動くピストンがついており,はじめピストンはストッパーの位置で静止している。風船とシリンダー内は液体で満たされており,液体の圧力 は一様で,液体の体積は一定とする。ゴム膜の厚みを無視し,係数 は一定とする。
(1)ピストンをゆっくりと動かし風船を膨らませたところ,図3-1のように半径が長さ だけ大きくなった。ピストンを動かすのに要した仕事を を用いて表せ。ただし, は十分小さく, の二次以上の項は無視してよい。
(2)設問 I(1) で風船を膨らませたときに,風船の表面積を大きくするのに要した仕事を を用いて表せ。ただし, は十分小さく, の二次以上の項は無視してよい。
(3) を を用いて表せ。ただし,ピストンを介してなされる仕事は,全て風船の表面積を大きくするのに要する仕事に変換されるものとする。
II
図3-2のように,小さな弁がついた細い管の両端に係数 の風船がついており,中には同じ温度の理想気体が封入され,気体の温度は常に一定に保たれている。
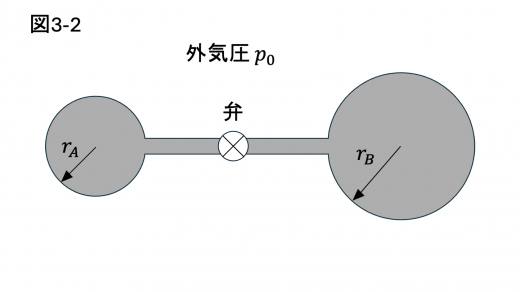
最初,弁は閉じており,風船の半径はそれぞれ である。管内と弁の体積,ゴム膜の厚みを無視し,係数 は一定とする。また,風船がしぼみきった場合,風船の半径は無視できるほど小さくなるものとする。
(1) の場合に弁を開いて起こる変化について,空欄 と に入る最も適切な語句を選択肢①〜④から選べ。また,下線部についての理由を簡潔に答えよ。
—
弁を開くと気体は管を通り,。十分時間が経った後の風船は,片方が半径 で,。
①大きい
②小さい
③他方も半径 になる
④他方はしぼみきっている
—
(2) を および,設問 II(1) で与えられた を用いて表せ。
III
実際の風船では,膜張力の大きさを特徴づける係数 は一定ではなく,半径 の関数として変化する。以下の設問では,風船の係数 は関係式
に従うと仮定する。ここで と は正の定数であり,温度によって変化しないものとする。風船の半径は より大きいものとする。
(1)図3-3のように,理想気体が封入され,風船の半径がどちらも の場合を考える。
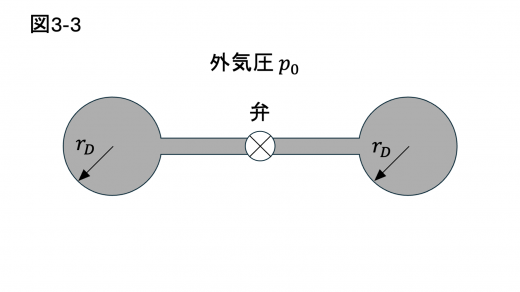
弁を開いて片方の風船を手でわずかにしぼませた後,手を放したところ,風船の大きさは変化し,半径が異なる二つの風船となった。 が満たすべき条件を答えよ。ただし,気体の温度は一定に保たれているものとする。
(2)設問 III(1) で十分時間が経った後,弁を開いたまま,二つの風船内の気体の温度をゆっくりとわずかに上げた。風船の内圧は高くなったか,低くなったか,理由と共に答えよ。必要ならば,図を用いてよい。
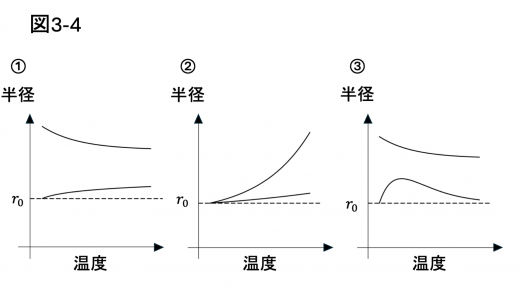
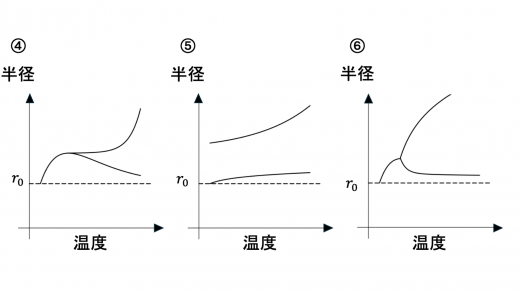
(3)設問 III(2) で十分時間が経った後,今度は風船内の気体の温度をゆっくりと下げた。二つの風船の半径を温度の関数として図示するとき,最も適切なものを図3-4の①〜⑥から一つ選べ。
解答例
解答例
設問 I
(1)
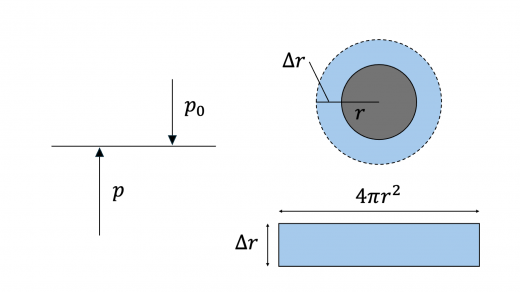
液体の温度および体積は一定であるので,状態方程式 (ボイル・シャルルの法則と状態方程式) より風船を膨らませている間も液体の圧力は で変わりません。 が十分小さいことより,ピストンを動かすのに要した仕事は,圧力 で面積 を距離 だけ動かす仕事と等しいとみることができます。
したがって,求める仕事 は
となります。
(2)
球の半径が と変化したときの球の表面積の変化を とすると, の二次以上の項を無視することより
したがって,与えられた公式より,求める仕事 は
となります。
(3)
問題文より,
であることがわかります。それぞれ代入して
と求められます。
設問 II
(1)
弁を開いた直後の左右の気体の圧力 は,それぞれ,I(3)の結果より
となります。いま より, であるから,気体は左側の風船から右側の風船に移動します。
:②小さい
そのまま時間が経過していっても,常に左側の風船の半径の方が右側の風船より小さく,したがって左側の風船内の気体の圧力の方が右側のそれより大きいため,気体は常に左側から右側へ移動し続けます。したがって,十分時間が経った後の風船は,片側が半径 で,他方はしぼみきっています。
:④他方はしぼみきっている
(2)
弁を開いた直後,半径が のときの左右の風船内の気体の体積をそれぞれ ,粒子数をそれぞれ とします。気体の温度を とすると,このとき各風船内の気体の状態方程式より
また,十分時間が経過したあと,粒子は全て半径 の一つの風船の中にあります。このときの気体の体積を とすると,状態方程式より
上の2式を最後の式に代入することで を消去できます。
球の体積の公式 (球の体積と表面積の公式の覚え方・積分での求め方) より計算すると, は
と求められます。
設問 III
(1)
設問 I では球の半径の変化は微少量で考えていたので,風船の半径 のときの風船の内圧 の公式は設問 III でも成り立つと考えます。すなわち は
と表されます。
とおき, の振る舞いを調べます。 の微分 (商の微分公式をわかりやすく【例題・証明・覚え方】) を求めると
したがって, の増減表 (増減表の書き方) は下図のようになります。
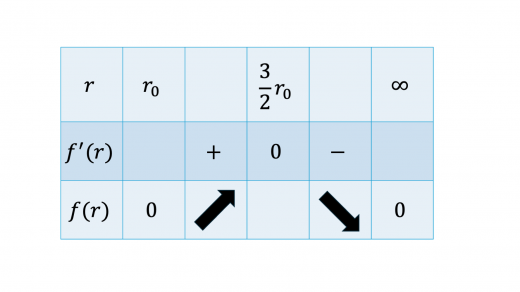
また, では
となります。
これより のグラフの概形を の関数として書くと,下図のようになります。
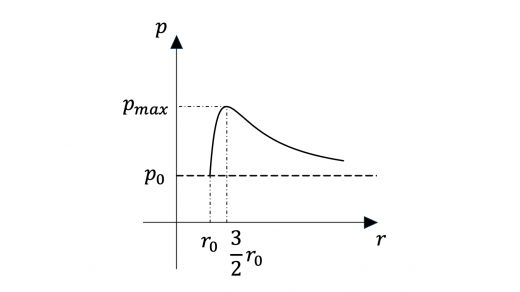
気体の温度は一定であることより,気体の圧力 と体積 について が成り立つことに注意します。弁を開いて片方の風船を手でわずかにしぼませた後手を離すと,両側の風船は上のグラフにしたがい, が等しくなるような異なる大きさの半径になります。
ここで, のときを考えます。
一方の風船をわずかにしぼませると,グラフより,大きい側の風船の圧力は小さい側の風船の圧力より大きくなるため,気体は大きい方の風船から小さい方の風船へと移動します。これより両側の風船の大きさが近づく方向に気体が移動するので,最終的に両側の風船の半径は へと戻ります。
一方, のときを考えます。
一方の風船をわずかにしぼませると,グラフより,大きい側の風船の圧力は小さい側の風船の圧力より小さくなります。したがって,気体は小さい方の風船から大きい方の風船へと移動します。これより両側の風船の大きさが遠ざかる方向に期待が移動するので,最終的に両側の風船の半径が異なる状態で定常状態となります。
したがって,求める条件は となります。
(2)
左右の風船の体積をそれぞれ とおきます。両側の風船内の気体全体の系を考えます。このとき気体の圧力を ,温度を とすると,ボイル・シャルルの法則より
が成り立ちます。
いま,気体の温度をゆっくりわずかに上げると,ボイル・シャルルの法則より も大きくなります。
ここで, なので,全体としてはおおよそ となります。
もし が大きくなるとすると,グラフより二つの風船の大きさは一定値に近づきます。したがって の値も一定値に近づきます。
一方,もし が小さくなるとすると,グラフより二つの風船のうち一方は小さくなり続け,もう一方は大きくなり続けます。したがって はどんどん大きくなります。
これより,風船の内圧 が小さくなる方に変化が進むと考えられます。
(3)
前問での議論より,はじめ両側の気体の圧力は最大値 に近づくように変化していきます。両側の気体の圧力が になったとき,両側の風船の半径はともに になります。
この後さらに気体の温度を下げていっても,気体の圧力は 以上には上がりません。しかし,前問での議論より,グラフにしたがって圧力が下がっていくのは気体の温度が上がるときなので,圧力が下がっていく変化も起こりません。したがって,温度を下げていっても気体の圧力は のまま一定です。
一方,気体全体ではボイル・シャルルの法則が成り立っていることより,温度を下げていくと,両側の風船の半径は同じままで小さくなっていきます。
これらの条件に合致するグラフは⑥です。
考察が難しい問題です。特に設問 III を本番中に正確に考えることは難しいと考えられます。もし本番で出たら,解ける問題を確実に解き,時間をかけすぎないようにする方が良いかもしれません。











