【解答・解説】東大物理2023 第1問 -力学-

以下の問題は，2023年度東京大学入試問題物理第1問から引用しています(一部見やすさのため修正しています)。

一見原子核の問題に見える問題ですが，その実ローレンツ力の概念などを用いる力学の問題です。

大問 I

(1)

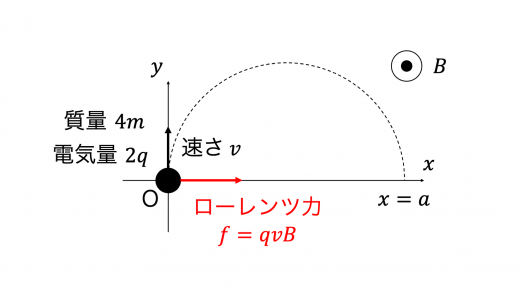
原子核は電荷を持った質点であり，磁場からはローレンツ力 (ローレンツ力の意味と式｜磁場中の荷電粒子の運動) を受けます。このローレンツ力は常に速度と垂直にはたらくので，原子核はローレンツ力を中心力とする等速円運動 (円運動とは｜円運動における加速度・向心力・遠心力を行います。

等速円運動の軌道を考えると，壁面に垂直に小窓を通過する原子核は，初速度が $y$ 軸正の方向を向いている原子核のみとなります。したがって，この円運動の半径 $r$ は

$$r = \dfrac{a}{2}$$

となります。

原子核の速さを $v$ とすると，運動方程式より

$$4 m \dfrac{v^2}{r} = 2 q v B$$

$$\begin{aligned} \therefore v &= \dfrac{1}{2} \dfrac{q B r}{m} \\ &= \dfrac{1}{4} \dfrac{q B a}{m} \end{aligned}$$

したがって，求める運動エネルギー $K$ は

$$\begin{aligned}K&= \dfrac{1}{2} 4m v^2 \\ &= \dfrac{1}{8} \dfrac{q^2 B^2 a^2}{m} \end{aligned}$$

となります。

(2)

(1)の軌道で等速円運動する原子核が小窓に到達する時間 $t$は，円運動の周期 $T_{\text{cir}}$ の1/2であり

$$t = \dfrac{1}{2} T_{\text{cir}}$$

ここで，(1)の円運動の角速度を $\omega$ とすると，$v = \dfrac{1}{2} a \omega$ より

$$\begin{aligned} T_{\text{cir}} &= \dfrac{2 \pi}{\omega} \\ &= \pi \dfrac{a}{v} \\ &= 4 \pi \dfrac{m}{q B} \end{aligned}$$

したがって，

$$t = 2 \pi \dfrac{m}{q B}$$

となります。ここで，X の半減期が $T$ であることより，時刻 $t$ に残っている X の割合は，

$$2^{- \dfrac{t}{T}} = 2^{- 2 \pi \dfrac{m}{q B T}}$$

これが $f$ 以上であることより

$$2^{- 2 \pi \dfrac{m}{q B T}} \geq f$$

$$\therefore -2 \pi \dfrac{m}{q B T} \geq \log_2 f = - \log_2 {\dfrac{1}{f}}$$

$0 < f < 1$ より，$\log_2 {\dfrac{1}{f}} > 0$ であることに注意してください。したがって，求める $B$ の下限値 $B_c$ は

$$B_c = \dfrac{2 \pi}{\log_2 {\dfrac{1}{f}}} \dfrac{m}{q T}$$

(3)

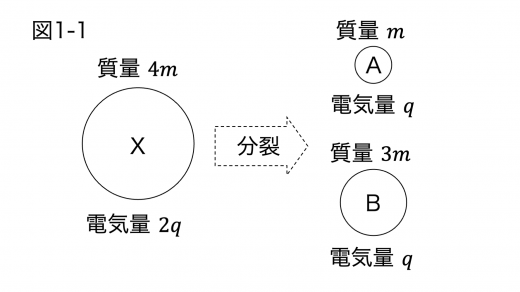
図1-1から，運動量保存則 (運動量保存則とエネルギー保存則の導出)より

$$m v_{\text{A}} = 3m v_{\text{B}}$$

$$\therefore v_{\text{A}} = 3 v_{\text{B}}$$

また，問題文中に，「分裂の際に，…質量欠損に対応するエネルギーが A と B の運動エネルギーとなる」と書いてあることより

$$(\Delta m) c^2 = \dfrac{1}{2} m v_{\text{A}}^2 + \dfrac{3}{2} m v_{\text{B}}^2$$

これらより $v_{\text{A}}, v_{\text{B}}$ について解いて

$$v_{\text{A}} = \sqrt{\dfrac{3}{2} \dfrac{\Delta m}{m}} c, \, v_{\text{B}} = \sqrt{\dfrac{1}{6} \dfrac{\Delta m}{m}} c$$

と求められます。

大問 II

(1)

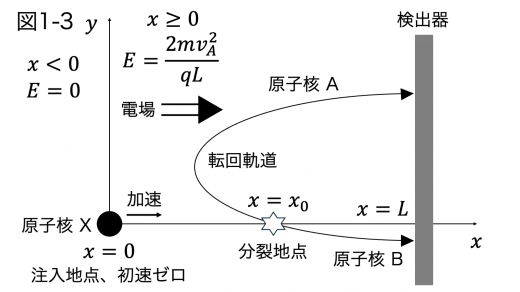
静止系での分裂前までの X の加速度を $a$ とすると，運動方程式より

$$4m a = 2q E = 4 \dfrac{m v_\text{A}^2}{L}$$

$$\therefore a = \dfrac{v_\text{A}^2}{L}$$

これより，時刻 $t$ での検出器に対する X の速さ $v$ および位置 $x$ は (等加速度運動・等加速度直線運動の公式)

$$v = a t, \, x = \dfrac{1}{2} a t^2$$

$x = x_0$ となるときの時刻を $t = t_0$ とすると

$$x_0 = \dfrac{1}{2} a t_0^2$$

$$\therefore t_0 = \sqrt{2 \dfrac{x_0}{a}}$$

このとき $v = \alpha v_\text{A}$ となります。したがって

$$\alpha v_\text{A} = a t_0 = \sqrt{2 a x_0} = \sqrt{2 \dfrac{x_0}{L}} v_\text{A}$$

$$\therefore \alpha = \sqrt{2 \dfrac{x_0}{L}} \tag{ア}$$

これより $x_0$ は，$\alpha$ を用いて

$$x_0 = \dfrac{1}{2} \alpha^2 L$$

と表されるので，$t_0$ は

$$\begin{aligned} t_0 &= \sqrt{\dfrac{\alpha^2 L}{a}} \\ &= \alpha \dfrac{L}{v_\text{A}} \tag{イ} \end{aligned}$$

検出器に対する A の初速度の $x, y$ 成分は，それぞれ

$$x : v_\text{A} \cos{\theta_0} + \alpha v_\text{A} = (\cos{\theta_0} + \alpha) v_\text{A}$$

$$y : v_\text{A} \sin{\theta_0}$$

と表されます。これが負であることより，$\theta_0$ に関する条件として

$$\cos{\theta_0} < - \alpha \tag{ウ}$$

と求められます。

これより，もし $- \alpha < -1$，すなわち $1 < \alpha$ であれば，転回軌道は実現しないことがわかります。(ア)より，$x_0$ に関する条件として

$$x_0 > \dfrac{1}{2} L \tag{エ}$$

が課されることがわかります。

さて，条件 (ウ) が満たされ，A が後方に飛ぶときを考えます。このとき検出器に対する A の運動を考えます。$x$ 軸方向の運動は，運動方程式より

$$m a_{\text{A}} = q E = \dfrac{2 m v_\text{A}^2}{L}$$

$$\therefore a_{\text{A}} = \dfrac{2 v_\text{A}^2}{L}$$

すなわち，この $a_{\text{A}}$ を加速度に持つ，初速度 $(\cos{\theta_0} + \alpha) v_{\text{A}}$ の等加速度運動を行います。検出器に対する A の速度 $V_\text{A}$ および 位置 $X_\text{A}$ は，分裂時を $t' = 0$ とすると，それぞれ

$$V_\text{A} = \dfrac{2 v_\text{A}^2}{L} t' + (\cos{\theta_0} + \alpha) v_{\text{A}}$$

$$X_\text{A} = \dfrac{ v_\text{A}^2}{L} t'^2 + (\cos{\theta_0} + \alpha) v_{\text{A}} t' + x_0$$

A が転回運動で $x < 0$ の領域に入らないための条件は，$X_\text{A}$ を $t'$ の2次方程式とみたときに実解を持たない条件と等しく，判別式に関する条件

$$D = (\cos{\theta_0} + \alpha)^2 v_\text{A}^2 - 4 \dfrac{ v_\text{A}^2}{L} x_0 < 0$$

転回運動が起こるとき $(\cos{\theta_0} + \alpha) < 0$ であることに注意して

$$-2 \sqrt{\dfrac{x_0}{L}} = - \sqrt{2} \alpha < \cos{\theta_0} + \alpha < 0$$

$$\therefore \cos{\theta_0} > - (1 + \sqrt{2}) \alpha \tag{オ}$$

式 (オ) が $\theta_0$ によらず成り立つような $x_0$ の条件は，$-1 > - (1 + \sqrt{2}) \alpha$，すなわち

$$\alpha = \sqrt{2 \dfrac{x_0}{L}} > \dfrac{1}{1 + \sqrt{2}}$$

$$\therefore x_0 > \dfrac{1}{2 (1 + \sqrt{2})^2 } L \tag{カ}$$

と求められます。

(2)

検出器に対する A の $y$ 軸方向の運動は，初速度 $v_{\text{A}} \sin{\theta_0}$ の等速運動となります。検出器の $x$ 軸上の点で観測されるのは，$\sin{\theta_0} = 0$，すなわち $\theta_0 = 0, \pi$ のときです。

• $\theta_0 = 0$ のとき

このとき分裂時の A の $x$ 軸方向の初速度は正なので，A は転回運動を起こさず，加速度 $a_{\text{A}}$ で $x$ 軸方向に等加速度運動を行うことがわかります。

$X_{\text{A}} = L$ となるような $t'$ を求めます。

$$\dfrac{v_\text{A}^2}{L} t'^2 + (1 + \alpha) v_\text{A} t' + x_0 = L$$

$$\therefore v_\text{A}^2 t'^2 + (1 + \alpha) v_\text{A} L t' + L (x_0 - L) = 0$$

$$\begin{aligned} \therefore t' &= \dfrac{- (1 + \alpha) v_\text{A} L + \sqrt{(1 + \alpha)^2 v_\text{A}^2 L^2 - 4 v_\text{A}^2 L (x_0 - L)}}{2 v_\text{A}^2} \, (\because t' > 0) \end{aligned}$$

このときの A の速度 $V_{\text{A}}$ は

$$\begin{aligned} V_{\text{A}} &= 2 \dfrac{v_{\text{A}}^2}{L} t' + V_0 \\ &= \dfrac{- (1 + \alpha) v_\text{A} L \pm \sqrt{(1 + \alpha)^2 v_\text{A}^2 L^2 - 4 v_\text{A}^2 L (x_0 - L)}}{L} + (1 + \alpha) v_{\text{A}} \\ &= \sqrt{(1 + \alpha)^2 - 4 \left( \dfrac{x_0}{L} - 1 \right)} v_\text{A} \\ &= \sqrt{(1 + \alpha)^2 - 4 \left( \dfrac{1}{2} \alpha^2 - 1 \right)} v_\text{A}\\ &= \sqrt{6 - (\alpha - 1)^2} v_\text{A} \end{aligned}$$

いま，転回軌道が起こらないことより，$0< x_0 < L$ であるから，$\alpha$ の範囲は

$$0 < \alpha < \sqrt{2}$$

この範囲で $\alpha$ を動かすと，$V_{\text{A}}$ の範囲は

$$\sqrt{5} v_\text{A} < V_{\text{A}} < \sqrt{6} v_\text{A}$$

したがって，A の運動エネルギー $K_{\text{A}}$ の取りうる範囲は

$$\dfrac{5}{2} m v_\text{A}^2 < K_{\text{A}} < 3 m v_\text{A}^2$$

• $\theta_0 = \pi$ のとき

このとき，分裂時の位置 $x_0$ によって A が転回運動するかが決まりますが，転回軌道が生じるか否かに関わらず，A が検出器に到達できるような $x_0$ の範囲は

$$\dfrac{1}{2 (1 + \sqrt{2})^2 } L < x_0 < L$$

$$\therefore \dfrac{1}{1 + \sqrt{2}} \alpha = \sqrt{2} - 1 < \alpha < \sqrt{2}$$

このときの速さ $V_\text{A}$ は

$$\begin{aligned} V_{\text{A}} &= \sqrt{(-1 + \alpha)^2 - 4 \left( \dfrac{1}{2} \alpha^2 - 1 \right)} v_\text{A} \\ &= \sqrt{6 - (\alpha + 1)^2 } v_\text{A} \end{aligned}$$

上記の範囲で $\alpha$ を動かしたとき，$V_\text{A}$ の範囲は

$$\sqrt{3 - 2 \sqrt{2}} v_\text{A} < V_\text{A} < 2 v_\text{A}$$

したがって，$K_\text{A}$ の範囲は

$$\dfrac{3 - 2 \sqrt{2}}{2} m v_\text{A}^2 < K_\text{A} < 2 m v_\text{A}^2$$

以上を合わせて，求める $K_\text{A}$ の範囲は

$$\dfrac{3 - 2 \sqrt{2}}{2} m v_\text{A}^2 < K_\text{A} < 2 m v_\text{A}^2 , \, \dfrac{5}{2} m v_\text{A}^2 < K_{\text{A}} < 3 m v_\text{A}^2$$

となります。

(3)(2)の結果を用いて考えてみます。$x$ 軸上のみで観測された A のうち，運動エネルギーが $m v_\text{A}^2$ より小さくなるのは，$\dfrac{3 - 2 \sqrt{2}}{2} < 1$ および (2) の議論より，$\theta_0 = \pi$ および $\sqrt{5} -1 < \alpha < \sqrt{2}$ のときとなります。

$x_0 = \dfrac{1}{2} \alpha^2 L$ より，これは $x_0$ が $L$ に近い領域で，A の運動エネルギーが $m v_\text{A}^2$ より小さくなることを意味しています。

検出器全体で考えても，分裂の位置について同様に考えられるので，分裂の位置 $x_0$ が検出器の位置 $L$ に近いほど，分裂後に検出器に到達する A の運動エネルギーは ($m v_\text{A}^2$ より) 小さくなると考えられます。

$\dfrac{L}{v_\text{A}}$ はおおよそ原子核 X が分裂せずに検出器の位置 $L$ に到達する時間だと考えられます。したがって，半減期 $T$ が $\dfrac{L}{v_\text{A}}$ と比べて長いほど，分裂の位置は $L$ に近づくと考えられます。

以上より，X の注入を繰り返し，A を検出したとき，運動エネルギーが $m v_\text{A}^2$ よりも短い原子核の数の割合は，X の半減期 $T$ が $L / v_\text{A}$ と比べてはるかに長い場合の方が，はるかに短い場合より多くなると期待されます。