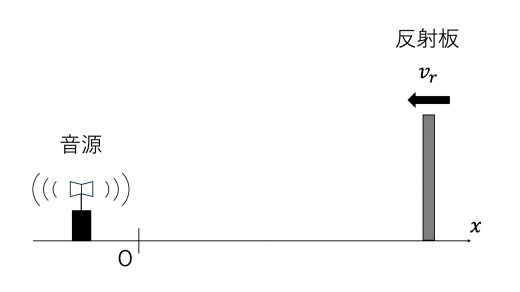【解答・解説】東大物理2024 第3問 -波動-

以下の問題は，2024年度東京大学入試問題物理第3問から引用しています。

ドップラー効果 (ドップラー効果の原理・公式・応用例)に関する問題です。一つ一つの局面で，音源・観測者の役割を持つものをそれぞれ確認しながら，丁寧に立式していきましょう。

設問 I

(1)

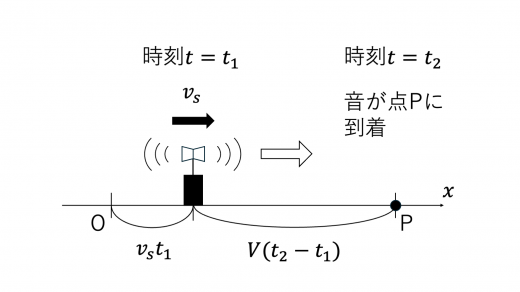
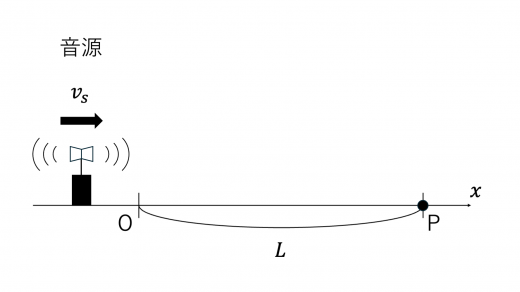
求める時刻を $t_2$ とします。

時刻 $t = t_1$ で音源から発せられた音が位置 $x = L$ に到達することより

$$t_1 = \dfrac{L}{V}$$

時刻 $t = t_1$ で音源は位置 $v_s t_1$ にあります。ここから $t_2 -t_1$ 後に音は音速で位置 $x = L$ に到達するので

$$v_s t_1 + V (t_2 - t_1) = L$$

$$\begin{aligned} \therefore t_2 &= \dfrac{L + (V - v_s)t_1}{V} \\ &= \dfrac{L}{V} + \dfrac{V - v_s}{V} t_1 \\ &= \left( 2 - \dfrac{v_s}{V} \right) \dfrac{L}{V} \end{aligned}$$

(2)

点 P で観測される音波の振動数について考えます。これは，点 P の位置にいる静止した観測者が，速さ $v_s$ で近づいてくる音源が発した振動数 $f_0$ の音波を観測するときの振動数となります。これを $f_0'$ とおくと，ドップラー効果の公式より

$$f_0' = \dfrac{V}{V - v_s} f_0$$

点 P での音波の位相 (位相（位相差・同位相・逆位相）)が $2 \pi$ だけ変化するために要する時間は，この音波の周期 $T$ に等しく，周期と振動数の関係より

$$T = \dfrac{1}{f_0'} = \dfrac{V - v_s}{V} \dfrac{1}{f_0} = \left( 1 - \dfrac{v_s}{V} \right) \dfrac{1}{f_0}$$

と求められます。

(3)

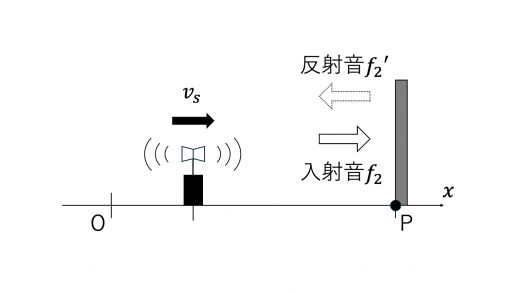
まず，反射板の位置で観測される音波の振動数 $f_2$ について考えます。これは，(2)での議論より

$$f_2 = \dfrac{V}{v - v_s} f_0$$

次に，音源の位置で観測される反射波の振動数 $f_2'$ について考えます。これは，静止した音源(=反射板)から振動数 $f_2$ で発せられる音波を，観測者が速さ $v_s$ で近づきながら観測したときの振動数に等しく

$$\begin{aligned} f_2' &= \dfrac{V + v_s}{V} f_2 \\ & = \dfrac{V + v_s}{V - v_s} f_0 (> f_0) \end{aligned}$$

振動数 $f_0, f_2'$ の2つの音波によるうなりの振動数 $f_h^1$ は，うなりの公式 (うなりの公式と例題)より

$$\begin{aligned} f_h^1 &= |f_2' - f_0| \\ &= f_2' - f_0 \\ &= \left( \dfrac{V + v_s}{V - v_s} - 1 \right) f_0 = \dfrac{2 v_s}{V - v_s} f_0 \end{aligned}$$

と求められます。

(4)

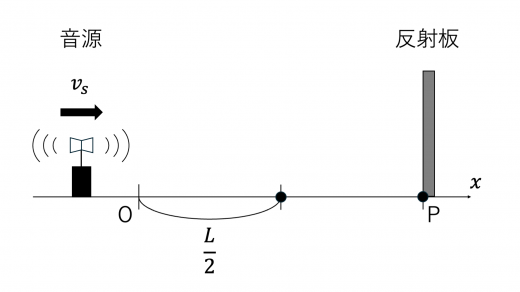
観測者は，音源からの音と反射板からの音を観測します。ここでは反射板は静止しているので，反射板の位置で観測された音をそのまま反射します。したがって，観測者が音源から聞く音と反射板の位置に入射する音が異なるときに，観測者の位置でうなりが観測されます。

ここで，ドップラー効果は音源あるいは観測者が「近づいているか，遠ざかっているか」によって公式が異なることに注意します。$x < \dfrac{L}{2}$ のとき，観測者と反射板いずれにとっても音源が「近づいてくる」状態のため，この範囲では観測者が音源から聞く音と反射板の位置に入射する音が同じであり，観測者はうなりを観測しません。

したがって，うなりが観測されるのは，音源が $x = \dfrac{L}{2}$ に到達した時刻以降となります。これを $t_3$ とすると

$$v_s t_3 = \dfrac{L}{2}$$

$$\therefore t_3 = \dfrac{1}{2} \dfrac{L}{v_s}$$

音源が $\dfrac{L}{2} < x (< L)$ の位置にあるとき，観測者が音源から直接聴く音，反射板に入射する音・反射する音の振動数をそれぞれ $f_3, f_4$ とします。

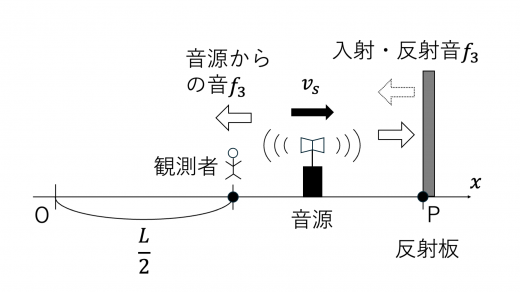
ドップラー効果の公式より，それぞれ

$$f_3 = \dfrac{V}{V + v_s} f_0$$

$$f_4 = \dfrac{V}{V - v_s} f_0$$

$v_s > 0$ より $f_3 < f_4$ であるから，観測されるうなりの振動数 $f_h^2$ は(この2は上付き添え字であり，2乗の意味ではありません)

$$\begin{aligned} f_h^2 &= |f_3 - f_4| \\ &= f_4 - f_3 \\ &= \left( \dfrac{V}{V - v_s} - \dfrac{V}{V + v_s} \right) f_0 \\ &= \dfrac{2 V v_s}{(V - v_s) (V + v_s)} f_0 \end{aligned}$$

と求められます。

設問 II

(1)

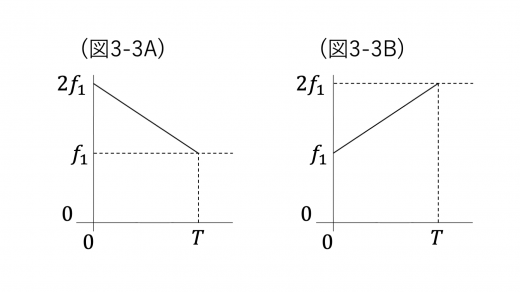
振動数が図 3-3(A) のように時間変化する場合の，時刻 $t$ で音源から発せられる音の振動数を $f_a (t)$ とすると

$$f_a (t) = \left( 2 - \dfrac{t}{T} \right) f_1$$

音速は振動数によらず常に一定で $V$ であることに注意してください。

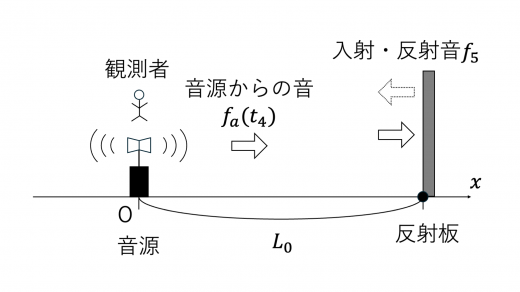
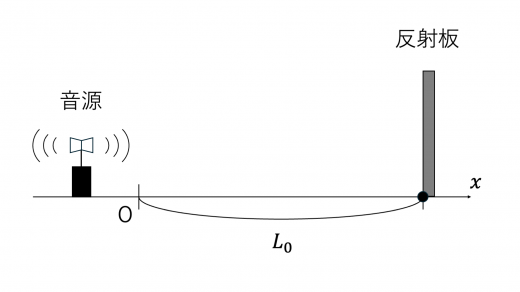
観測者は，時刻 $t = 0$ で音源から発せられた音が反射されて原点に帰ってきたときの音と，音が原点に帰ってきた4ときの時刻 $t = t_4$ で音源から発せられる音 (振動数 $f_a (t_4)$) とのうなりを観測します。

音源と反射板は静止しているので

$$t_4 = \dfrac{2 L_0}{V}$$

です。

時刻 $t = 0$ で音源から発せられた音を反射板の位置で観測するときの振動数・反射音の振動数を $f_5$ とすると，

$$f_5 = f_a (0) = 2 f_0$$

一方

$$f_a (t_4) = \left( 2 - \dfrac{t_4}{T} \right) f_1$$

したがって，観測者が観測するうなりの振動数 $f_h$ は

$$\begin{aligned} f_h &= |f_5 - f_a (t_4)| \\ &= \dfrac{t_4}{T} f_0 \\ &= 2 \dfrac{L_0}{V T} f_0 \end{aligned}$$

ゆえに，$L_0$ は

$$L_0 = \dfrac{1}{2} \dfrac{f_h}{f_0} V T$$

と求められます。

(2)

観測者は，時刻 $t = 0$ で発せられた音が反射板で反射され，時刻 $t = t_{\text{A} 0}$ に原点に帰ってきた音と，その時刻に音源から発せられる音 (振動数 $f_a (t_{\text{A} 0}$)) とのうなりを観測します。

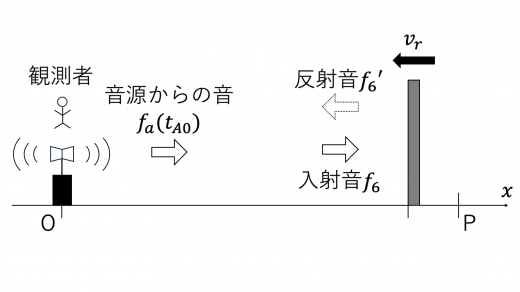
時刻 $t = 0$ で発せられた音を反射板で観測するときおよび反射板で反射された音を原点で観測するときの振動数をそれぞれ $f_6, f_6'$ とします。

まず，時刻 $t_{\text{A} 0}$ は

$$t_{\text{A} 0} = \dfrac{2 L_\text{A}}{V}$$

次に，$f_6, f_6'$ について考えます。反射板は静止している音源に向かって速さ $v_r$ で運動しているので

$$f_6 = \dfrac{V + v_r}{V} f_a (0)$$

$$f_6' = \dfrac{V}{V - v_r} f_6 = \dfrac{V + v_r}{V - v_r} f_a (0) = \dfrac{V + v_r}{V - v_r} 2 f_1$$

また，$f_a (t_{\text{A} 0})$ は

$$f_a (t_{\text{A} 0}) = \left( 2 - \dfrac{t_{\text{A} 0}}{T} \right) f_1 = 2 \left( 1 - \dfrac{L_\text{A}}{V T} \right) f_1$$

式の形より

$$f_6' > 2 f_1 > f_a (t_{\text{A} 0})$$

であることがわかるので，求めるうなりの振動数 $f_h^3$ は

$$\begin{aligned} f_h^3 &= f_6' - f_a (t_{\text{A} 0}) \\ &= 2 \left[ \dfrac{V + v_r}{V - v_r} - \left( 1 - \dfrac{L_\text{A}}{V T} \right) \right] f_1 \\ &= 2 \left( 2 \dfrac{v_r}{V - v_r} + \dfrac{L_\text{A}}{V T} \right) f_1 \end{aligned}$$

となります。

(3)

振動数が図 3-3(B) のように時間変化する場合の，時刻 $t$ で音源から発せられる音の振動数を $f_b (t)$ とすると

$$f_b (t) = \left( 1 + \dfrac{t}{T} \right) f_1$$

と表されます。

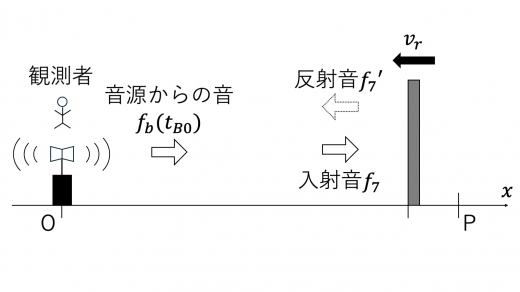
観測者は，時刻 $t = t_s$ で音源から発せられた音が反射板で反射され，原点に帰ってきた音と，そのときの時刻 $t = t_\text{B}$ で音源から発せられる音 (振動数 $f_b (t_\text{B})$) とのうなりを観測します。

上図のように，時刻 $t = t_s$ で発せられた音を反射板で観測するときおよび反射板で反射された音を原点で観測するときの振動数をそれぞれ $f_7, f_7'$ とします。

反射板は静止している音源に向かって速さ $v_r$ で運動しているので

$$f_7 = \dfrac{V + v_r}{V} f_b (t_s)$$

$$f_7' = \dfrac{V}{V - v_r} f_7 = \dfrac{V + v_r}{V - v_r} f_b (t_s) = \dfrac{V + v_r}{V - v_r} \left( 1 + \dfrac{t_s}{T} \right) f_1$$

また，$t_B = t_s + \dfrac{2 L_B}{V}$ に注意して

$$f_b (t_\text{B}) = \left( 1 + \dfrac{t_\text{B}}{T} \right) f_1 = \left( 1 + \dfrac{t_s}{T} + 2 \dfrac{ L_B}{V T}\right)$$

したがって，観測されるうなりの振動数 $f_h^4$ は

$$\begin{aligned} f_h^4 &= |f_b (t_B) - f_7'| \\ &= f_b (t_B) - f_7' \quad (\text{後述}) \\ &= \left( 1 + \dfrac{t_s}{T} + 2 \dfrac{ L_B}{V T} \right) f_1 - \left( 1 + 2 \dfrac{v_r}{V-v_r} \right) \left( 1 + \dfrac{t_s}{T} \right) f_1 \\ &= 2 \left[ \dfrac{ L_B}{V T} - \dfrac{v_r}{V-v_r} \left( 1 + \dfrac{t_s}{T} \right)\right] f_1 \end{aligned}$$

(4)

まず，$f_h^A$ は $f_h^3$ に等しく

$$f_h^A = f_h^3 = 2 \left( 2 \dfrac{v_r}{V - v_r} + \dfrac{L_A}{V T} \right) f_1$$

次に，$f_h^B$ について考えます。$f_h^A$ と $f_h^B$ を同時に観測するので，$f_h^B$ は $f_h^4$ について $t_s = 0$ とすればよいことになります。$t_s = 0$ のとき $L_B = L_A$ に注意して

$$f_h^B = f_h^4 (t_s = 0, L_A = 0) = 2 \left( \dfrac{L_A}{V T} - \dfrac{v_r}{V - v_r} \right) f_1 < f_h^A$$

したがって，求める振動数の差 $\Delta f_h$ は

$$\begin{aligned} \Delta f_h &= |f_h^A - f_h^B| \\ &= f_h^A - f_h^B \\ &= 6 \dfrac{v_r}{V - v_r} f_1 \end{aligned}$$

と求められます。

(5)

(4)の結果より

$$\Delta f_h = 6 \dfrac{v_r}{V - v_r} f_1$$

$$\therefore \Delta f_h (V - v_r) = 6 v_r f_1$$

$$\begin{aligned} \therefore (\Delta f_h + 6 f_1) v_r = \Delta f_h V \end{aligned}$$

$$\begin{aligned} \therefore v_r &= \dfrac{\Delta f_h}{\Delta f_h + 6 f_1} V \\ &= \dfrac{1}{1 + 6 \dfrac{f_1}{\Delta f_h}} V \end{aligned}$$

ここで

$$\begin{aligned} 6\dfrac{f_1}{\Delta f_h} &= 6 \cdot \dfrac{3.0 \times 10^4}{5.0 \times 10^2} \\ &= 360 \end{aligned}$$

であるので

$$\begin{aligned} v_r &= \dfrac{1}{361} \cdot 3.4 \times 10^2 = 0.941 \end{aligned}$$

有効数字2桁で求めると，$v_r = 0.94 [\text{m/s}]$ と求められます。