【解答・解説】東大物理2024 第2問 -電磁気-

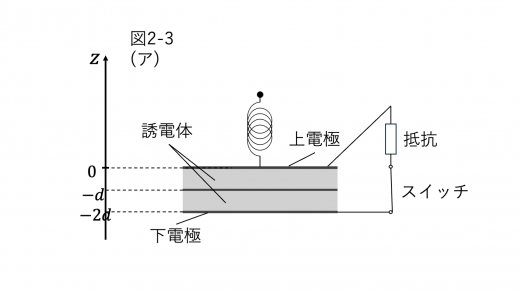
大問 I

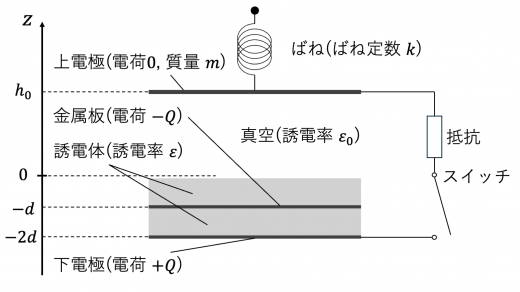
(1)下電極が電位の基準となっていることに注意します。

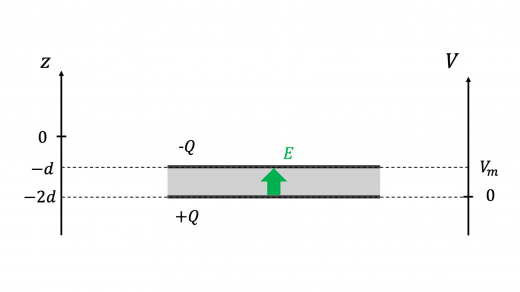
金属板と下電極からなるコンデンサーを考えます。このコンデンサーの電気容量 $C$ は (コンデンサーの理論)

$$C = \dfrac{\varepsilon L^2}{d}$$

と与えられるので，金属板と下電極との電位差 $V$ は

$$V = \dfrac{Q}{C} = \dfrac{Q d}{\varepsilon L^2}$$

金属板・下電極が蓄えている電荷の正負より，金属板の方が下電極より電位が低い (電位の考え方については 等電位線(等電位面)の重要性質と例題｜電気力線との関係 などを参照) ので，下電極を電位の基準としたときの金属板の電位 $V_m$ は

$$V_m = -V = - \dfrac{Q d}{\varepsilon L^2}$$

と求められます。

(2)スイッチを閉じて定常状態になったのち，下図のように電荷が蓄えられているとします。

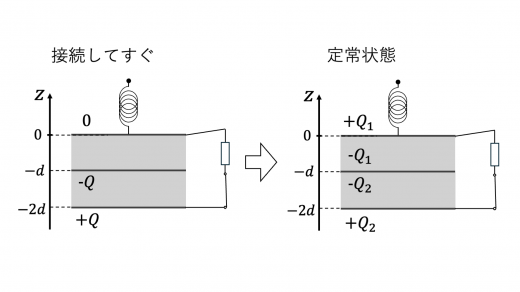
上電極・下電極の電荷量保存則 (電荷と電気量保存の法則) より

$$Q_1 + Q_2 = Q \tag{1-1}$$

回路内でキルヒホッフ第2法則 (キルヒホッフの法則の解説と例題) より

$$\dfrac{Q_1}{C_1} = \dfrac{Q_2}{C_2} \tag{1-2}$$

ここで，上電極と金属板，金属板と下電極をそれぞれ誘電体が挿入されたコンデンサー (詳しくは 誘電率 を参照) とみなし，それぞれ電気容量を $C_1, C_2$ としています。いま

$$C_1 = C_2 = \dfrac{\varepsilon L^2}{d}$$

であるので，(2-2)より

$$Q_1 = Q_2$$

したがって，(2-1)より

$$Q_1 = Q_2 = \dfrac{Q}{2}$$

(3)上電極がつりあいの位置にあるとき，ばねののびが $l_0$ であるとします。力のつりあいより

$$k l_0 = mg \tag{1-3}$$

スイッチを開いてから上電極を移動させているので，(電荷量保存則より) 上電極および下電極に蓄えられた電荷量は不変です。

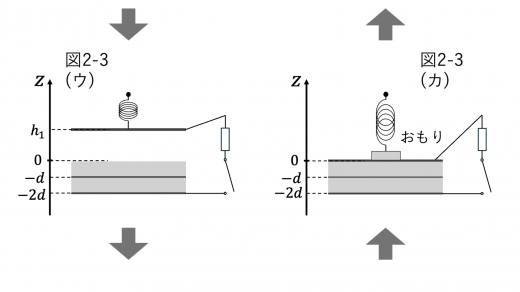
いま，上電極の $z$ 座標が $z = z_1$ であったとします。簡単のため，まず $z_1 < h_0$ とします。

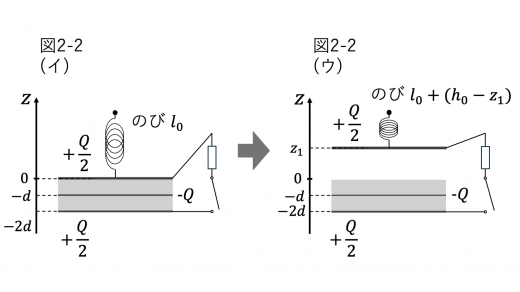
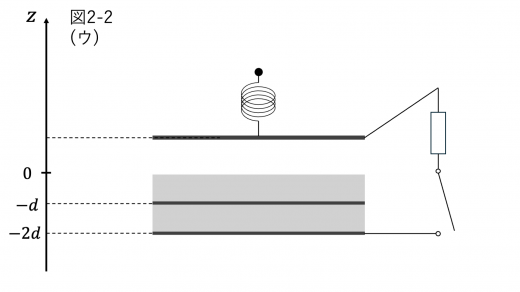
上電極に加わる力はばねの慣性力，重力，コンデンサーの極板間引力の3つです。まず，ばねの慣性力から考えます。図(イ)の状態から図(ウ)の状態に移る際，上図のように，つりあいの位置と比べてばねは $h_0 - z_1$ だけさらにのびることになります。したがって，$z$ 軸正の向きを力の正の方向とすると，ばねの慣性力は $k (l_0 + h_0 - z_1)$ となります。これは $z_1 <h_0$ としても同様の表現となります。

((注)さらに付け加えると，$z_1 - h_0 < l_0$ であっても，縮んでいる状態をマイナス分だけのびていると考えれば，同様の表現で表すことが可能です。)

次に，上電極と金属板の間にはたらくクーロン力 $f_Q$ を考えます。上電極と金属板は電荷 $\dfrac{Q}{2}$ を蓄えるコンデンサーとみなすことができます。上電極にはたらく電場 $E$ は

$$E = \dfrac{\dfrac{Q}{2}}{\varepsilon_0 L^2} = \dfrac{Q}{2 \varepsilon_0 L^2}$$

と書くことができるので，コンデンサーの極板間引力公式 (コンデンサーの理論) より

$$f_Q = \dfrac{1}{2} \dfrac{Q}{2} \dfrac{Q}{2 \varepsilon_0 L^2} = \dfrac{1}{8} \dfrac{Q^2}{ \varepsilon_0 L^2}$$

と求められます。したがって，上電極に対する力のつりあいより

$$k (l_0 + h_0 - z_1) = mg + \dfrac{1}{8} \dfrac{Q^2}{ \varepsilon_0 L^2} \tag{1-4}$$

(1-3)式より

$$k (h_0 - z_1) = \dfrac{1}{8} \dfrac{Q^2}{ \varepsilon_0 L^2}$$

$$\therefore z_1 = h_0 - \dfrac{1}{8} \dfrac{Q^2}{ k \varepsilon_0 L^2}$$

と求められます。

(注)この式変形より $h_0 - z_1 > 0$ であることもわかります。

(4)誘電体中と真空中で電場の大きさが変わることに注意します。

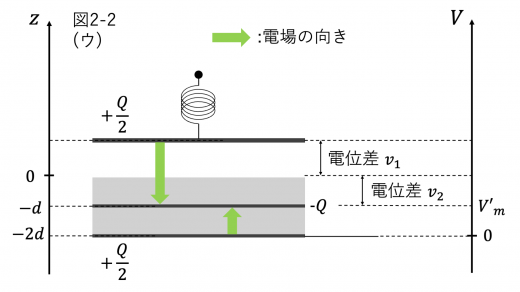
まず，$z = z_1$ と $z = 0$ との電位差 $v_1$ を求めます。上電極と誘電体表面とを1つのコンデンサーとみなしたときの電気容量を $C_3$ とすると

$$v_1 = \dfrac{\dfrac{Q}{2}}{C_3} = \dfrac{Q z_1}{2 \varepsilon_0 L^2}$$

同様に，$z = 0$ と $z = -d$ との電位差 $v_2$ を求めます。誘電体表面と金属板とを1つのコンデンサーとみなしたときの電気容量を $C_4$ とすると

$$v_2 = \dfrac{\dfrac{Q}{2}}{C_4} = \dfrac{Q d}{2 \varepsilon L^2}$$

また，金属板の電位 $V_m'$ は，I(1)と同様にして

$$V_m' = - \dfrac{\dfrac{Q}{2}}{C_2} = - \dfrac{Q d}{2 \varepsilon L^2}$$

$z = z_1$ から $z = -d$ まで，電場は $z$ 軸負の方向を向いているので，下電極を基準としたときの上電極の電位 $V_u$ は

$$\begin{aligned} V_u &= v_1 + v_2 + V_m \\ &= \dfrac{Q z_1}{2 \varepsilon_0 L^2} + \dfrac{Q d}{2 \varepsilon L^2} - \dfrac{Q d}{2\varepsilon L^2} \\ &= \dfrac{Q}{2 \varepsilon_0 L^2} \left( h_0 - \dfrac{1}{8} \dfrac{Q^2}{ k \varepsilon_0 L^2} \right) \end{aligned}$$

(別解)スイッチを切る前まで，$z = 0$ の上電極と ($z = -2d$ の) 下電極とが導線でつながれていたので，このとき上電極と下電極の電位は等しく0になっています。電荷の移動が終わったのちスイッチを切り，上電極を $z$ 軸正の方向に動かしても，$-2d \leq z \leq 0$ で電場は変わらないため，このときも $z = 0$ の電位は0となっています。すなわち，求める電位は $v_1$ に等しく，

$$V_u = v_1 = \dfrac{Q z_1}{2 \varepsilon_0 L^2} = \dfrac{Q}{2 \varepsilon_0 L^2} \left( h_0 - \dfrac{1}{8} \dfrac{Q^2}{ k \varepsilon_0 L^2} \right)$$

と求められます。

大問II

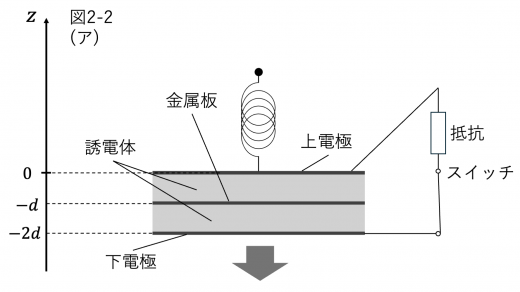
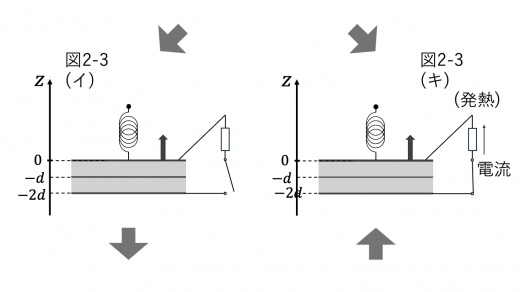
(1)(ア)の状態で定常状態となったとき，上電極および下電極に蓄えられる電荷はIの結果より $\dfrac{Q}{2}$ となります。

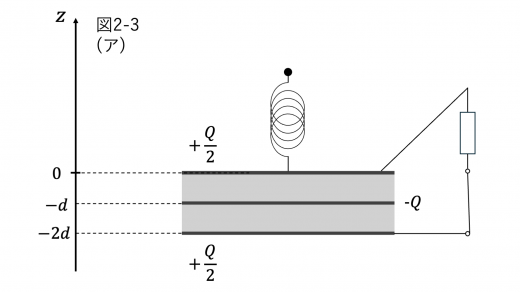
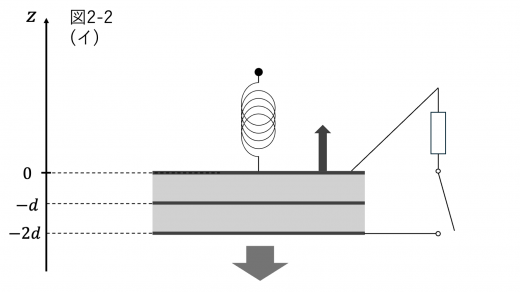
(イ)のあと，上電極が位置 $z$ にある場合の，上電極にはたらく力を考えてみましょう。

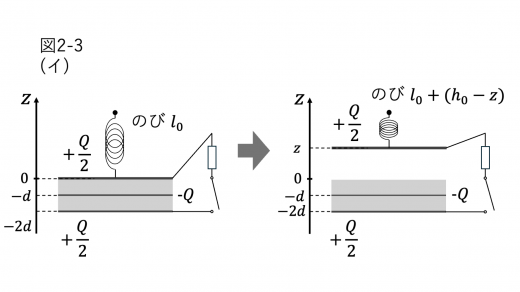
上電極にはたらく力は，ばねの慣性力 $F$，上電極の重力 $mg$，クーロン力 $f_Q$ となります。Iと同様に考えることで，$F$ は $z$ 軸上向きを正として，

$$F = k \{l_0 + (h_0 - z) \}$$

また $f_Q$ は $z$ 軸上向きを正として，

$$f_Q = \dfrac{1}{2} \dfrac{Q}{2} E = \dfrac{1}{8} \dfrac{Q^2}{ \varepsilon_0 L^2}$$

とそれぞれ表すことができます。

これらより，上電極の運動方程式は

$$\begin{aligned} m \ddot{z} &= k \{l_0 + (h_0 - z) \} - mg - f_Q \\ &= -k \left( z - h_0 + \dfrac{f_Q}{k} \right) \\ &= -k (z - z_1) \end{aligned}$$

この式と，ばねの単振動についての考察 (ばねの単振動の解説) より，上電極は $z = z_1$ を中心とした単振動をすることがわかります。初め上電極は静止していたことから，$z = 0$ は単振動の最下点であることがわかるので，この単振動の振幅 $A$ は $A = z_1$ であることがわかります。

上昇を始めてから上電極の速度が0になるのは，上電極が単振動の最上点にやってきたときになります。したがって，

$$h_1 = 2 A + 0 = 2 z_1 = 2 \left( h_0 - \dfrac{1}{8} \dfrac{Q^2}{ k \varepsilon_0 L^2} \right)$$

と求められます。

(2)スイッチをつないでから発熱が止むまで，エネルギー保存則が成り立ちます。系の位置エネルギーおよびばねが蓄えるエネルギーは発熱の過程で変わらないので，コンデンサーが蓄える静電エネルギーの変化が発熱量の合計 $W$ になります (熱力学第一法則｜仕事と内部エネルギーの関係)。

スイッチをつないだ直後および発熱が止んだときの系の静電エネルギーを，それぞれ $U_1, U_2$ とします。

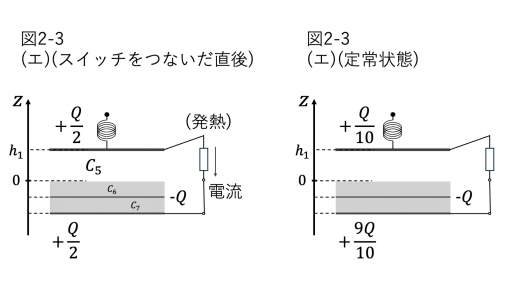
上図のようにコンデンサーの電気容量をそれぞれ $C_5, C_6, C_7$ とすると，それぞれ

$$C_5 = \dfrac{\varepsilon_0 L^2}{h_1}, C_6 = C_7 = \dfrac{\varepsilon L^2}{d}$$

と書くことができます。

これより $U_1$ は

$$\begin{aligned} U_1 &= \dfrac{1}{2} \dfrac{\left( \dfrac{Q}{2} \right)^2}{C_5} + \dfrac{1}{2} \dfrac{\left( \dfrac{Q}{2} \right)^2}{C_6} + \dfrac{1}{2} \dfrac{\left( \dfrac{Q}{2} \right)^2}{C_7} \\ &= \dfrac{1}{8} \dfrac{Q^2 h_1}{\varepsilon_0 L^2} + \dfrac{1}{4} \dfrac{Q^2 2d}{\varepsilon L^2} \end{aligned}$$

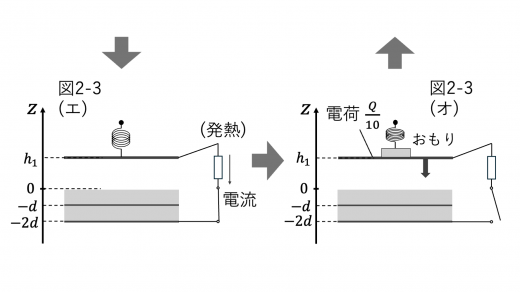
次に $U_2$ を考えます。スイッチをつないでから定常状態になったときに，上電極の蓄える電荷が $\dfrac{Q}{10}$ となったとき，電荷量保存則より，下電極の蓄える電荷は$\dfrac{9}{10} Q$ となります。したがって

$$\begin{aligned} U_2 &= \dfrac{1}{2} \dfrac{\left( \dfrac{Q}{10} \right)^2}{C_5} + \dfrac{1}{2} \dfrac{\left( \dfrac{Q}{10} \right)^2}{C_6} + \dfrac{1}{2} \dfrac{\left( \dfrac{9}{10} Q \right)^2}{C_7} \\ &= \dfrac{1}{200} \dfrac{Q^2 h_1}{\varepsilon_0 L^2} + \dfrac{41}{100} \dfrac{Q^2 d}{\varepsilon L^2} \end{aligned}$$

エネルギー保存則より，求める発熱量の合計 $W_1$ は

$$\begin{aligned} W_1 &= U_1 - U_2 \\ &= \dfrac{3}{25} \dfrac{Q^2 h_1}{\varepsilon_0 L^2} - \dfrac{4}{25} \dfrac{Q^2 d}{\varepsilon L^2} \\ &= \dfrac{1}{25} \dfrac{Q^2}{L^2} \left( \dfrac{3 h_1}{\varepsilon_0} - \dfrac{4 d}{\varepsilon} \right) \end{aligned}$$

(3)再びスイッチを開いてから，上電極・下電極が蓄える電荷量は不変で，それぞれ $\dfrac{Q}{10}, \dfrac{9Q}{10}$ となります。

おもりの質量を $M$ とし，おもりと上電極の系の運動方程式を考えます。

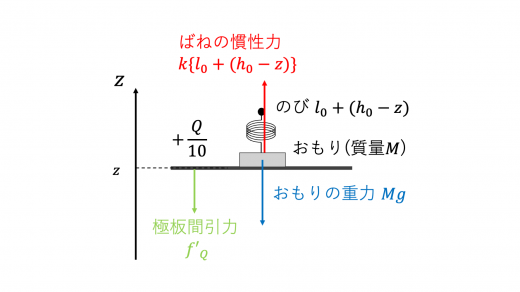
前問II(1)と同様に考えると，この系にはたらく力はばねの慣性力，系の重力，上電極が受けるクーロン力 $f_Q'$となります。

ここで，上電極にはたらく電場 $E'$ は

$$E' = \dfrac{\dfrac{Q}{10}}{\varepsilon_0 L^2} = \dfrac{Q}{10 \varepsilon_0 L^2}$$

であるので，コンデンサーの極板間引力の公式より

$$f_Q' = \dfrac{1}{2} \dfrac{Q}{10} E' = \dfrac{1}{200} \dfrac{Q^2}{\varepsilon_0 L^2}$$

したがって，系が位置 $z$ にあるときの運動方程式は

$$\begin{aligned} m \ddot{z} &= k (l_0 + h_0 - z) - (M + m) g - f_Q' \\ &= -k \left( z - h_0 + \dfrac{Mg}{k} + \dfrac{1}{200} \dfrac{Q^2}{k \varepsilon_0 L^2} \right) \end{aligned}$$

したがって，系は位置 $z = z_2 = h_0 - \dfrac{Mg}{k} - \dfrac{1}{200} \dfrac{Q^2}{k \varepsilon_0 L^2}$ を中心とした単振動をすることがわかります。

上電極が下降を始めてから速度が0になった位置が $z = 0$ であることより，この単振動はII(1)の単振動と運動の範囲が一致していることがわかります。したがって，II(1)の単振動と中心が一致していなければなりません。

したがって

$$z_2 = z_1$$

$$\therefore h_0 - \dfrac{Mg}{k} - \dfrac{1}{200} \dfrac{Q}{k \varepsilon_0 L^2} = h_0 - \dfrac{1}{8} \dfrac{Q^2}{ k \varepsilon_0 L^2}$$

$$\therefore M = \dfrac{3}{25} \dfrac{Q^2}{g \varepsilon_0 L^2}$$

(注)$M$ が正しく質量の次元になっているかを確認します。上式より

$$Mg = \dfrac{3}{25} \dfrac{Q^2}{ \varepsilon_0 L^2}$$

右辺の次元は，極板間引力の次元と一致しているので，左辺の次元も力の次元と一致します。したがって，$M$ は質量の次元となっています。

(4)おもりを取り除いてスイッチを閉じてから発熱がやむまで，エネルギー保存則が成り立ちます。したがって，(2)同様，静電エネルギーの変化を考えれば，(キ)→(ア)の過程での発熱量の合計 $W_2$ がわかります。1サイクルでの抵抗の発熱量の合計 $W_{tot}$ は，$W_{tot} = W_1 + W_2$ として求めることができます。

では，$W_2$ を求めていきましょう。

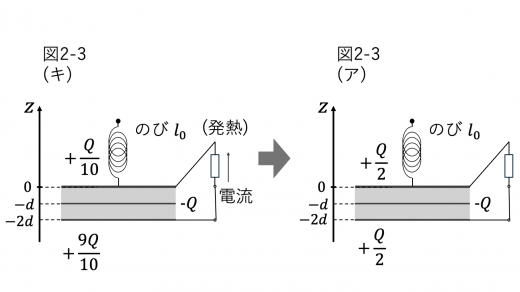
スイッチを閉じた直後と発熱が止んだときの系の静電エネルギーをそれぞれ $U_3, U_4$ とします。

上図で示されている上電極と金属板，および金属板と下電極はそれぞれコンデンサーとみなせ，その静電容量 $C$ は

$$C = \dfrac{\varepsilon L^2}{d}$$

と表せることに注意します。上図より

$$\begin{aligned} U_3 &= \dfrac{1}{2} \dfrac{\left( \dfrac{Q}{10} \right)^2}{C} + \dfrac{1}{2} \dfrac{\left( \dfrac{9Q}{10} \right)^2}{C} \\ &= \dfrac{41}{100} \dfrac{Q^2}{C} \end{aligned}$$

$$\begin{aligned} U_4 &= \dfrac{1}{2} \dfrac{\left( \dfrac{Q}{2} \right)^2}{C} + \dfrac{1}{2} \dfrac{\left( \dfrac{Q}{2} \right)^2}{C} \\ &= \dfrac{25}{100} \dfrac{Q^2}{C} \end{aligned}$$

これより $W_2$ は

$$\begin{aligned} W_2 &= U_3 - U_4 \\ &= \dfrac{4}{25} \dfrac{Q^2}{C} = \dfrac{4}{25} \dfrac{Q^2 d}{\varepsilon L^2} \end{aligned}$$

ゆえに，1サイクルでの抵抗の発熱量の合計 $W_{tot}$ は

$$\begin{aligned} W_{tot} &= W_1 + W_2 \\ &= \dfrac{1}{25} \dfrac{Q^2}{L^2} \left( \dfrac{3 h_1}{\varepsilon_0} - \dfrac{4 d}{\varepsilon} \right) + \dfrac{4}{25} \dfrac{Q^2 d}{\varepsilon L^2} \\ &= \dfrac{3}{25} \dfrac{Q^2 h_1}{\varepsilon_0 L^2} \end{aligned}$$

と求められます。

(別解)1サイクル全体でのエネルギーの流れを考えます。系全体と外部とのエネルギーのやり取りは，外部からおもり(の位置エネルギー)を加えることと，抵抗からの発熱の2つのみです。したがって，エネルギー保存則より

$$\begin{aligned} W_{tot} &= M g h_1 \\ &= \dfrac{3}{25} \dfrac{Q^2 h_1}{\varepsilon_0 L^2} \end{aligned}$$

と求められます。