誘電率
コンデンサーの静電容量に登場する,誘電率という物理定数について取り上げます。また誘電率と比誘電率の関係についても解説します。
この記事に関連するQ&A
誘電率とは
誘電率とは
誘電率と静電容量
コンデンサーの静電容量 は,コンデンサーの極板の面積 ,高さ との間に
という関係があります(この関係について,詳しくは コンデンサーの理論 をご覧ください)。
このときの比例定数 (イプシロン)を,(真空の)誘電率と呼びます。
誘電率の単位
誘電率の単位についても軽く復習しておきましょう。静電容量の公式より,誘電率の単位は の単位と一致します。静電容量の単位はファラド [F] であり,これを用いると,誘電率の単位は
と表すことができます。
一方,誘電率の単位を SI (国際単位系) を用いて表すこともできます。この場合,ファラドの SI 表記を用いて
と表すことができます。こちらも,詳しく知りたい方は コンデンサーの理論 を併せてご覧ください。
誘電率と比誘電率
誘電率と比誘電率
比誘電率とは
物体は,その材質に応じて,その物体固有の誘電率を持っています。この物体の誘電率は,真空の誘電率との比を用いて評価します。すなわち,ある物体の誘電率 は,真空の誘電率 を用いて
と表すことができます。この比例定数 を比誘電率と呼びます。
種々の物質の比誘電率
真空の誘電率は, であることがわかっています。
種々の物質の比誘電率の一部を紹介します。空気の比誘電率はほぼ1,水の比誘電率は80程度,ポリエチレンの比誘電率は2.3程度です。
応用: コンデンサー
応用: コンデンサー
以下の例題を通じて,コンデンサー内の誘電体のふるまいを計算してみましょう。
極板面積 ,高さ ,静電容量 のコンデンサーに,下図のように電圧 の電源につなぎ,定常状態になったあと,電源を取り外すことを考える。
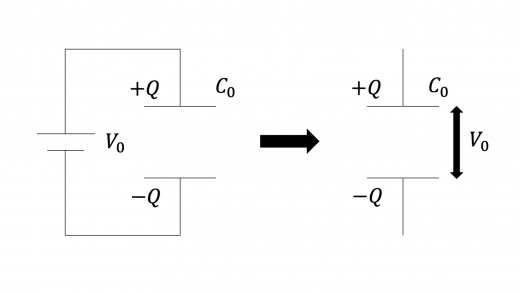
このコンデンサーに底面積 ,高さ ,比誘電率 の誘電体を完全に挿入する。以下の問いに答えよ。
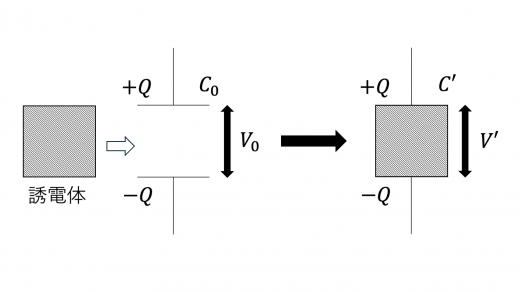
(1)誘電体を挿入したあとのコンデンサーの静電容量 を求めよ。
(2)誘電体を挿入したあとの誘電体内の電場の強さ を求めよ。
(3)誘電体を挿入したことによる仕事 を求めよ。
(1)コンデンサーの静電容量 は,静電容量の公式において,真空の誘電率 を誘電体の誘電率 と置き換えることで得られます。つまり
すなわち,コンデンサーを比誘電率 の誘電体で満たすと,その静電容量は 倍になることがわかります。
(この結果より,比誘電率は,その物体がどれだけ電荷を蓄えられるかの指標となっていると考えることもできます。)
(2)誘電体を挿入したあとのコンデンサーに加わっている電圧を求められれば,そこから電場を求めることができます。
電源を取り外しているので,誘電体の挿入前後でコンデンサーに蓄えられている電荷の総量 は変わりません。コンデンサーの公式より,
誘電体を挿入したあと,コンデンサーに加わっている電圧を とすると,コンデンサーの公式より
が成り立ちます。(1),(2),(3)式より
誘電体内では電場は一定と考えてよいので,誘電体内の電場 は
と求めることができます。
(3)誘電体の挿入前後のコンデンサーの静電エネルギーの差が,求める仕事 となります。
誘電体を挿入する前のコンデンサーの静電エネルギー は,公式より
誘電体を挿入したあとのコンデンサーの静電エネルギー は,同様にして
と求められます。
これより,求める仕事は
となります。
比誘電率は,例題のように,コンデンサーに誘電体を挿入する場合などに特に現れます。煩雑になりやすいので,問題を通して慣れておくとよいです。











