コンデンサーの直列・並列接続

初めに，コンデンサー(キャパシタ)の静電容量 $C$ について簡単に復習しておきます。

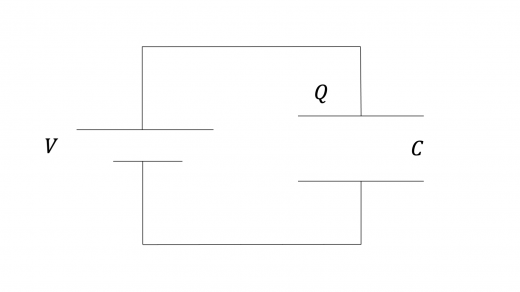
上図のように，静電容量 $C$ のコンデンサーに電荷 $Q$ が蓄えられており，電圧 $V$ が加わっているとき，これらの物理量の間には

$$Q = CV \tag{☆}$$

という関係があったのでした。詳しくは コンデンサーの理論 をご覧ください。 直列/並列接続されたコンデンサーの合成容量を求めるときも，この関係式を用います。

また，コンデンサーの静電容量 $C$ と その底面積 $S$，高さ $d$，真空の誘電率 $\varepsilon_0$ との間には，

$$C = \varepsilon_0 \dfrac{S}{d} \tag{☆☆}$$

という関係式がありました。 コンデンサー内部に誘電体を挿入する場合には，こちらの関係式も利用します。

2つの場合

下図(S1)のように，静電容量がそれぞれ $C_1, C_2$ の2つのコンデンサーを直列に接続した回路を考えます。これらのコンデンサーを1つのコンデンサーとみなしたときの合成容量 $C_s$ を求めてみます。

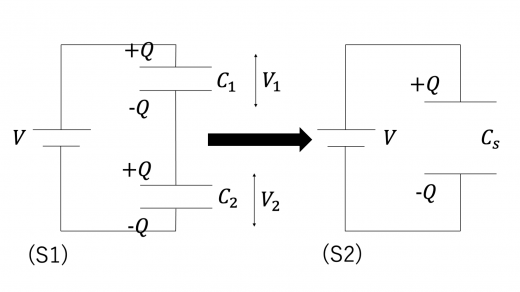
はじめ，どちらのコンデンサーも電荷を蓄えていないとします。上図の回路 S1 において，定常状態のとき，上のコンデンサーに蓄えられる電荷が $Q$ であったとすると，下のコンデンサーに蓄えられる電荷は，下図の赤実線内での電気量保存の法則(詳しくは電荷と電気量保存の法則)より $Q$ となります。

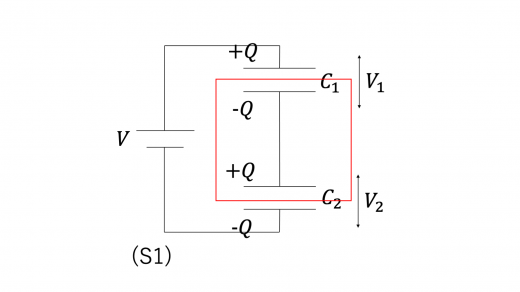
これより，各コンデンサーに加わっている電圧 $V_1, V_2$ は，それぞれ

$$V_1 = \dfrac{Q}{C_1}, \, V_2 = \dfrac{Q}{C_2}$$

となります。キルヒホッフの第二法則(詳しくはキルヒホッフの法則の解説と例題)より

$$V - V_1 - V_2 = 0$$

$$\therefore V = V_1 + V_2 = Q \left(\dfrac{1}{C_1} + \dfrac{1}{C_2} \right)$$

$$\therefore Q = \dfrac{1}{\dfrac{1}{C_1} + \dfrac{1}{C_2}} V \tag{1}$$

一方，これらのコンデンサーを静電容量が $C_s$ の1つのコンデンサーとみなしたとき，そのコンデンサーが蓄えている電荷は $Q$，加わっている電圧は $V$ であるので

$$Q = C_s V \tag{2}$$

が成り立っています。(1)式と(2)式を見比べて

$$C_s = \dfrac{1}{\dfrac{1}{C_1} + \dfrac{1}{C_2}} \quad \therefore \dfrac{1}{C_s} = \dfrac{1}{C_1} + \dfrac{1}{C_2}$$

つまり，直列接続の場合の合成容量の逆数は，それぞれのコンデンサーの静電容量の逆数の和として求められます。

3つ以上の場合

まず，3つの場合を考えてみます。下図のように，静電容量がそれぞれ $C_1, C_2, C_3$ のコンデンサーを直列に接続した場合の合成容量 $C_s'$ を求めてみましょう。

まず，左の2つを1つのコンデンサーとみなします。この合成容量 $C'$ は，先ほどの公式により

$$\dfrac{1}{C'} = \dfrac{1}{C_1} + \dfrac{1}{C_2}$$

として求められます。

次に，静電容量 $C', C_3$ のコンデンサーを1つのコンデンサーとみなして，全体として1つのコンデンサーとみなします。この合成容量 $C_s'$ は，再び先ほどの公式より

$$\begin{aligned} \dfrac{1}{C_s'} &= \dfrac{1}{C'} + \dfrac{1}{C_3} \\ &= \dfrac{1}{C_1} + \dfrac{1}{C_2} + \dfrac{1}{C_3} \end{aligned}$$

と求められます。

一般に，静電容量が $C_1, C_2, ... , C_n$ の $n$ 個のコンデンサーを直列に接続したときの合成容量 $C_s^n$は，同様にして

$$\dfrac{1}{C_s^n} = \sum_{k = 1}^{n} \dfrac{1}{C_k}$$

と求められます。

2つの場合

下図のように，下図のように，静電容量がそれぞれ $C_1, C_2$ のコンデンサーを並列に接続した場合の合成容量 $C_p$ を求めてみましょう。

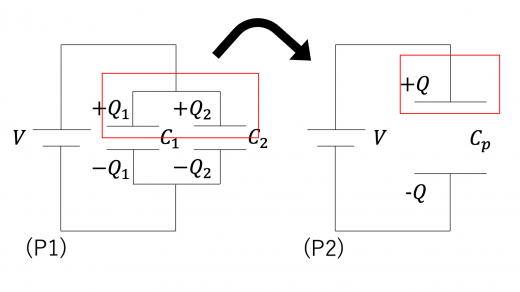
上図の回路 P1 において，それぞれのコンデンサーが蓄える電荷を $Q_1, Q_2$ とします。キルヒホッフ第二法則より各コンデンサーに加わる電圧は $V$ と等しいので，各物理量には

$$Q_1 = C_1 V, \, Q_2 = C_2 V$$

という関係があります。これらのコンデンサーが蓄えている電荷の合計は，赤実線部の電荷量保存則より $Q = Q_1 + Q_2$ となるので，代入して

$$Q = Q_1 + Q_2 = (C_1 + C_2) V \tag{3}$$

一方，これらのコンデンサーを，静電容量が $C_p$ の1つのコンデンサーとみなしたとき，そのコンデンサーが蓄えている電荷は $Q$，加わっている電圧は $V$ であるので

$$Q = C_p V \tag{4}$$

という関係が成り立ちます。

(3)式と(4)式を見比べて

$$C_p = C_1 + C_2$$

つまり，並列接続の場合の合成容量は，それぞれのコンデンサーの静電容量の和として求められます。

3つ以上の場合

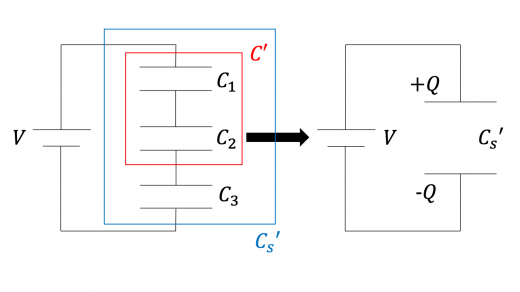
まず，3つの場合を考えます。下図のように，静電容量がそれぞれ $C_1, C_2, C_3$ の3つのコンデンサーを並列に接続した場合の合成容量を求めてみます。

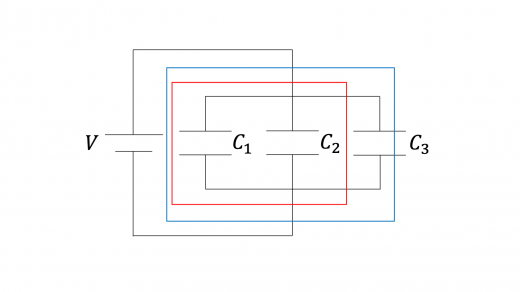
初めに，左の2つのコンデンサー(上図の赤枠内)を1つとみなします。このコンデンサーの合成容量 $C'$ は，先ほどの公式より

$$C' = C_1 + C_2$$

と求められます。

次に，静電容量 $C', C_3$ の2つのコンデンサーを1つのコンデンサーとみなして(上図の青枠内)，全体として1つのコンデンサーと考えます。このコンデンサーの合成容量 $C_p'$ は，先ほどの公式から

$$C_p' = C' + C_3 = C_1 + C_2 + C_3$$

と求められます。

より一般に，静電容量が $C_1, C_2, \, ... \, C_n$ の $n$ 個のコンデンサーを並列に接続したときの合成容量 $C_p^n$ は，同様にして

$$C_p^n = \sum_{k = 1}^{n} C_k$$

と求めることができます。

コンデンサー内をすべて誘電体に置き換えたときの静電容量は，誘電率を誘電体の誘電率 $\varepsilon$ に置き換えることで求められます。

一方，コンデンサーに(それより小さい)誘電体を挿入したとき，誘電体が挿入された部分とそれ以外の部分を静電容量が異なるコンデンサーとして考えることで，コンデンサーの直列/並列接続の考え方を使うことができます。

以下の2つのパターンを例に取り，合成容量の求め方を確認していきます。

• (A)高さは同じだが，底面積が異なる誘電体を挿入する

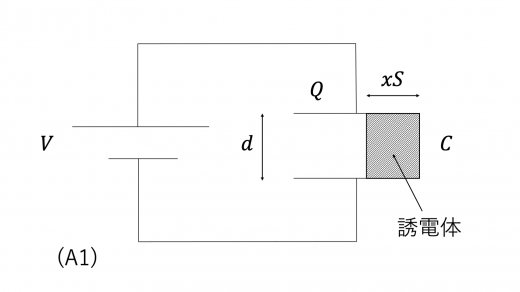
• (B)底面積は同じだが，高さが異なる誘電体を挿入する

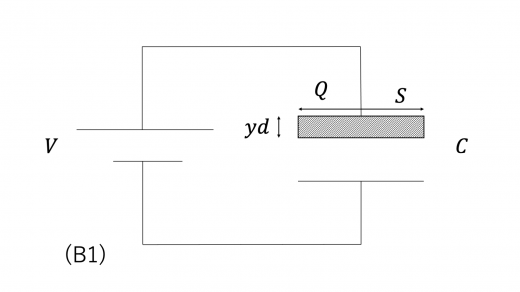
以下では，用意するコンデンサーは全て静電容量 $C$，底面積 $S$，高さ $d$ であるとし，誘電体の誘電率は $\varepsilon = \varepsilon_r \varepsilon_0$ であるとします。

(A)底面積が異なる誘電体を挿入する

上図(A1)のように，底面積 $xS$，高さ $d$ の誘電体を，端が極板の端と一致するように挿入したとします。このとき，下図(A2)のように，元々のコンデンサーを分解していくつかのコンデンサーで構成されると考えます。

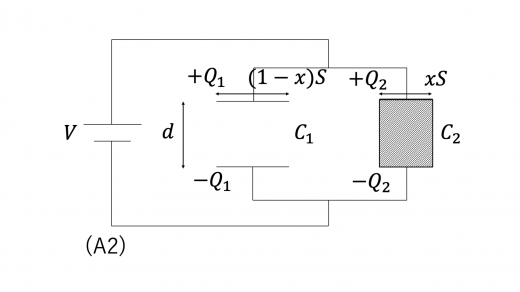
このとき，電気量保存則が成り立っていることに注意します。すなわち元のコンデンサーが蓄えていた電荷 $Q$ と，分解後の各コンデンサーが蓄えている電荷 $Q_1, Q_2$ との間には

$$Q = Q_1 + Q_2$$

という関係が成り立っています。

各コンデンサーの静電容量 $C_1, C_2$ は，それぞれ

$$C_1 = \varepsilon_0 \dfrac{(1-x)S}{d} = (1-x)C$$

$$C_2 = \varepsilon \dfrac{xS}{d} = \varepsilon_r \varepsilon_0 \dfrac{xS}{d} = \varepsilon_r x C$$

これらのコンデンサーは並列に接続されていると考えられるので，全体として1つのコンデンサーとみなしたときの合成容量，つまり誘電体を挿入後のコンデンサーの静電容量 $C_a$ は，公式より

$$C_a(x) = C_1 + C_2 = [(1-x) + \varepsilon_r x] C$$

と求めることができます。

例えば，底面積がコンデンサーの半分の誘電体を図(a1)の位置に挿入する場合の静電容量は，$x = 1/2$ を代入して

$$C_a \left(\dfrac{1}{2} \right) = \left(\dfrac{1}{2} + \varepsilon_r \dfrac{1}{2} \right) C = \dfrac{1 + \varepsilon_r}{2} C$$

となります。

(B)高さが異なる誘電体を挿入する

上図(B1)のように，底面積 $S$，高さ $yd$ の誘電体を，端が極板の端と一致するように挿入したとします。このとき，下図(B2)のように，元々のコンデンサーを分解していくつかのコンデンサーで構成されると考えます。

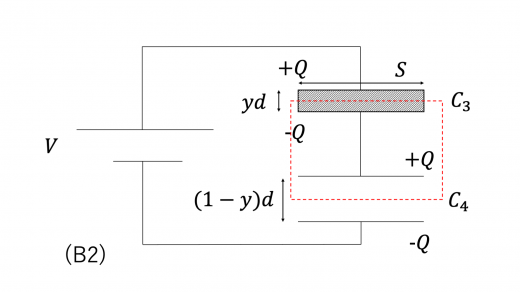
このときも，分解前後で電気量保存則が成り立っていることに注意してください。まず，分解前のコンデンサーが蓄えている電荷 $Q$ と，図(B2)上のコンデンサーが蓄えている電荷は等しいです。さらに，図(B2)の赤破線の部分の電気量保存より，図(B2)下のコンデンサーが蓄える電荷も $Q$ となります。

さて，図(B2)の各コンデンサーの静電容量をそれぞれ $C_3, C_4$ とすると，(☆☆)より

$$C_3 = \varepsilon \dfrac{S}{yd} = \varepsilon_r \varepsilon_0 \dfrac{S}{yd} = \varepsilon_r \dfrac{1}{y} C$$

$$C_4 = \varepsilon_0 \dfrac{S}{(1-y)d} = \dfrac{1}{1-y} C$$

これらのコンデンサーは直列に接続されていると考えられるため，全体として1つのコンデンサーとみなしたときの合成容量，つまり元のコンデンサーの静電容量 $C_b$ は，公式より

$$\begin{aligned} \dfrac{1}{C_b} &= \dfrac{1}{C_3} + \dfrac{1}{C_4} \\ &= \left[\dfrac{1}{\varepsilon_r} y + (1-y) \right] \dfrac{1}{C} \\ &= \dfrac{y + \varepsilon_r (1-y)}{\varepsilon_r} \dfrac{1}{C} \end{aligned}$$

$$\therefore C_b(y) = \dfrac{\varepsilon_r}{y + \varepsilon_r (1-y)} C$$

と求めることができます。

例えば，高さが半分の誘電体を図(b1)の位置に挿入する場合の静電容量は，$y = 1/2$ を代入して

$$C_b \left(\dfrac{1}{2} \right) = \dfrac{\varepsilon_r}{\dfrac{1}{2} + \varepsilon_r \dfrac{1}{2}} C = \dfrac{2 \varepsilon_r}{1 + \varepsilon_r} C$$

となります。

コンデンサー内に導体が挿入されているときは，導体を導線として考えて，問題を解けばよいです。

例えば下図(d1)のように導体が挿入されている場合は，下図(d2)のようにコンデンサーを分解すればよいです。

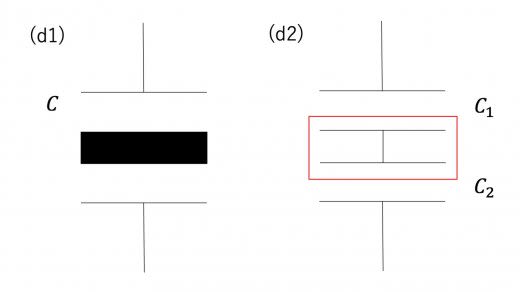
ただし，導線部で電気量保存則が成り立っていることに注意してください。これは，上図(d2)において，赤枠内の電気量保存則が成り立っていることに相当します。

抵抗にも直列接続と並列接続が存在し，合成抵抗を考えることができたのでした。簡単に公式を復習しておきましょう(別記事にて詳しく解説予定です)。

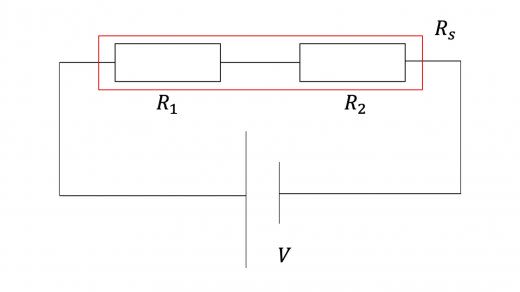
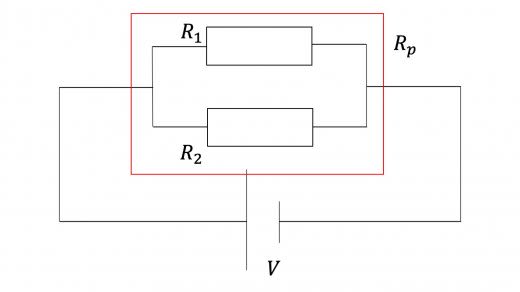
合成抵抗を求める際，直列・並列接続のどちらでそのまま和をとるか，逆数の和をとるかが，合成容量を求める場合とは逆になっているのに注意が必要です。

ただ公式を丸暗記するのではなく，その導出までできるようにしておくのが望ましいですね。