等電位線(等電位面)の重要性質と例題｜電気力線との関係

更新 2022/02/09

この記事では，等電位線について解説します。まず電位の定義をしっかり押さえて，例題を通して等電位線について深く理解しましょう。

この問題の(1)番のDHを求める問題で、三角形DMAを切り出して、直線AMに垂直になるように、DHを降ろしていますが、 2

2022年慶応志木の問題です。大問▪️3の(2)番で、このような問題がありました。ここで図を書くと、添付図のようにな 3

問あなたの今の気持ちを伝える文を書こう。という問題に下記の様に答えを書きました。 ●Im glad that giv 4

エタノール（C2H5OH）の量論比での酸化反応式と理論空燃比を求めよ A) 化学反応式 B) 理論空燃比 5

電位・等電位線・等電位面の定義

等電位線を理解するためには，当然電位の定義を正確に理解しておかなければなりません。ここで電位の定義をあらためて復習しておきましょう。

電位の定義

単位電荷あたりの，電場によるポテンシャルエネルギーを電位と定義する。
すなわち基準点からある地点へ単位電荷を運んだときの，単位電荷にはたらく電気力につりあわせる外力のする仕事の逆符号である。

電位の具体例や詳しい解説が以下の記事でなされています。
電位の定義｜エネルギーとしての解釈・具体例

等電位線に話を戻します。等電位線はその名の通り，電位の等しい点を結んだ線のことをいいます。それ以上でもそれ以下でもありません。シンプルな定義ですが，等電位線を書くことで，物理系を視覚化でき，より詳しい理解につながります。

なお，3次元で等電位となる点の集合を考えると，一般に面になることが予想されます。これを等電位面と呼びます。以下では簡単のために等電位線を例として解説しますが，等電位面についても同じような議論を行うことができます。

等電位線と電気力線

等電位線の定義を上で紹介しましたが，電場を視覚的に捉えようとする概念では，他にも電気力線がありました。
電気力線の定義・性質・書き方の例
電気力線と等電位線の関係はどうなっているでしょうか。実は，以下の重要な定理があります。

定理

電気力線と等電位線は直交する。

証明

電気力線と等電位線等電位線と電気力線が角度 $\theta$ で交わっているとする。等電位線と電気力線が交わる点に単位電荷をおき，その点から等電位線に沿って単位電荷を微小距離 $dl$ だけ動かす。このとき電場のする仕事は $1\cdot E\cos\theta dl=Edl\cos\theta$ となる。等電位線の定義より、この仕事は $0$ に等しい。よって $\theta=\dfrac{\pi}{2}$ を得る。

この定理が，等電位面は電場に直交するように描いておけばいいことを保証してくれます。これが非常に重要な点です。

等電位線の例題

以下では，いくつかの系に対して等電位線を具体的に書いてみることで，等電位線への理解を深めましょう。

例題1

点電荷の周りには，一様等方な電場ができる。この電場に対する等電位線をかけ。

解答

以下のようになる。オレンジ色の線が電気力線，黒色の線が等電位線を表す。点電荷の周りの等電位線

意識するべきことは，等電位線が電気力線に直交するという定理です。

例題２

以下のような一様電場の系に対する電気力線が与えられている。この系の等電位線をかけ。一様電場の電気力線

解答

以下のようになる。オレンジ色の線が電気力線，黒色の線が等電位線を表す。一様電場のつ電位線

例題３

以下のように，電気力線と電位 $V_1,V_2$ に対応する等電位線が与えられている。電位 $\dfrac{V_1+V_2}{2}$ に対応する等電位線をかけ。

ヒント：電気力線の密度は電場の強さに対応している。密度が大きいところほど，電場は強い。

解答

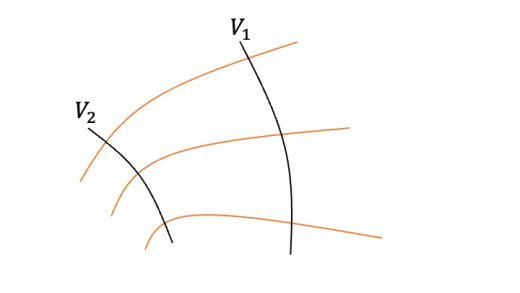
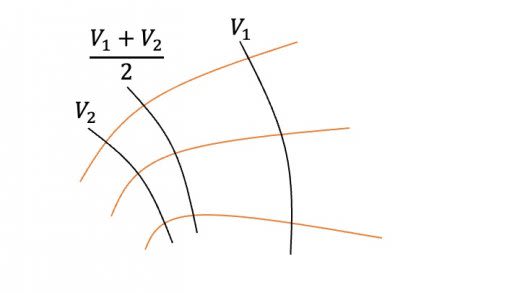
電気力線に沿って $V_1$ から $V_2$ に移動するとき，ちょうど $\dfrac{V_1+V_2}{2}$ となる地点を考える。電場は $V_2$ に近いところの方が強いので， $\dfrac{V_1+V_2}{2}$ となる地点は，中点よりもやや $V_2$ よりになる。よって以下の図のようになる。等電位線と電気力線の密度

大学入試では，等電位線を扱う問題はあまり出ませんが，この記事で紹介した知識は頭に入れておくと良いでしょう。