電気振動

振動回路とは

振動回路(あるいはLC振動回路)とは，コイルとコンデンサーが並列に接続された回路のことです。回路図では，例えば下図のように表されます。

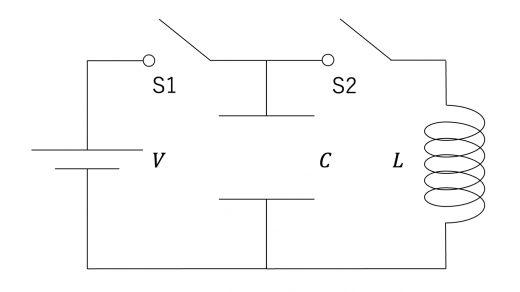
電池の電圧を $V$，コンデンサーの電気容量を $C$，コイルの自己インダクタンスを $L$ とします。また，S1とS2はスイッチを指しています。

回路の電流の考察

まず，スイッチ S1 をオンにし，スイッチ S2 をオフにします。

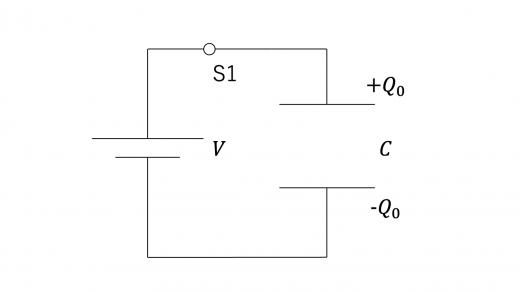
回路が定常状態になったとき，コンデンサーに蓄えられる電荷 $Q_0$ は，コンデンサーの公式 (詳しくはコンデンサーの理論) より

$$Q_0 = CV$$

と求められます。

次に，回路が定常状態になったのち，スイッチ S2 をオンにし，スイッチ S1 をオフにします。

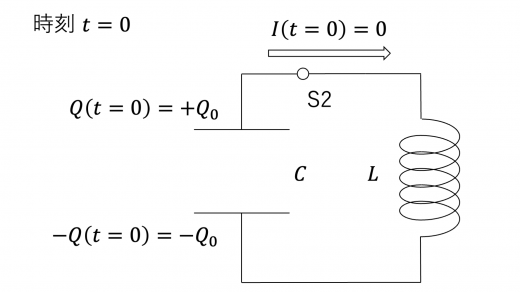
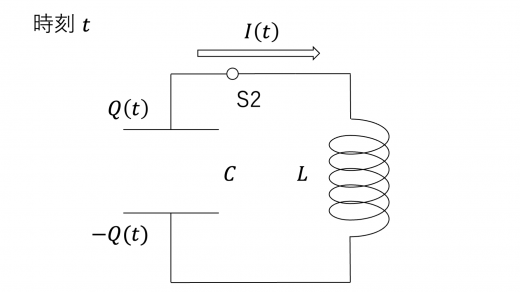
スイッチをつなぎかえた時刻を $t = 0$ とし，時刻 $t$ での回路の挙動を見てみましょう。時刻 $t$ でコンデンサーが蓄えている電荷および回路に流れている電流を，それぞれ $Q(t), I(t)$ とします。

まず，コンデンサー第二法則 (詳しくはキルヒホッフの法則の解説と例題) より

$$\dfrac{Q(t)}{C} = L \dfrac{d I}{d t} \tag{1}$$

また，電荷保存則 (詳しくは電荷と電気量保存の法則) より，コンデンサーが蓄えている電荷量の時間変化(のマイナス)が電流となると考えられるので

$$I(t) = - \dfrac{d Q}{dt} \tag{2}$$

(2)式を(1)式に代入して

$$\dfrac{Q(t)}{C} = - L \dfrac{d^2 Q}{d t^2}$$

$$\therefore Q = - C L \dfrac{d^2 Q}{d t^2} \tag{3}$$

(3)式は力学の単振動の分野で出てくる微分方程式と数学的に同じ構造をしています。ばねの単振動の解説 や 単振動のまとめ より，(3)式の解は

$$Q(t) = Q_0 \cos{\omega t}, \omega = \dfrac{1}{\sqrt{CL}} \tag{4}$$

のように求められます。ここで求めた $\omega$ を共振角周波数，この $\omega$ から求められる周波数　$f = \dfrac{1}{2 \pi \sqrt{L C}}$ を共振周波数と呼びます。上式からわかるように，共振角周波数および共振周波数は，回路のコンデンサーの電気容量とコイルの自己インダクタンスによってのみ求めることができます。

(2)・(4)式より，時刻 $t$ に回路を流れる電流 $I(t)$ は

$$\begin{aligned} I(t) &= - \dfrac{d}{dt} Q_0 \cos{\omega t} \\ &= - (- \omega Q_0 \sin{\omega t}) \\ & = \omega Q_0 \sin{\omega t} = \dfrac{Q_0}{\sqrt{L C}} \sin{\omega t} \end{aligned} \tag{5}$$

と求めることができます。

また，電荷および電流の周期 $T$ は

$$T = \dfrac{2 \pi}{\omega} = 2 \pi \sqrt{L C}$$

と求めることができます。

このように，振動回路では，回路内を流れる電流が $\sin{}$ のかたち で表され，時刻変化とともに振動することがわかります。この現象を電気振動と呼び，回路を流れる電流を振動電流と呼びます。

振動回路の系の振る舞いを1周期で図示すると，下図のようになります。

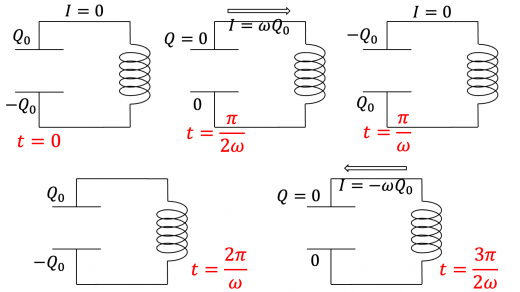
回路内で電荷や電流が1周期ごとに振動していることが視覚的にもわかります。

共振という用語については，気柱の振動と共鳴現象｜固有振動数や開口端補正の解説 や LC・RLC共振回路の共振周波数の求め方 も併せてご覧ください。

エネルギー保存則

スイッチをS1からS2に切り替えた後，回路には外部から仕事がされないので，エネルギー保存則が成り立っているはずです。これを確認しましょう。

考えるべきエネルギーは，コンデンサーが蓄える電荷の静電エネルギー $U_C$ と，コイルを流れる電流による磁気エネルギー(詳しくはコイルのエネルギーとエネルギー密度の解説) $U_L$ です。

時刻 $t= 0$ では，それぞれ

$$\begin{aligned} U_C &= \dfrac{Q(0)^2}{2C} \\ &= \dfrac{Q_0}{2C} \end{aligned}$$

$$\begin{aligned} U_L &= \dfrac{1}{2} L I(0)^2 \\ &= 0 \end{aligned}$$

と求められます。したがって，回路の全エネルギー $U_{tot}$ は

$$U_{tot} (0) = U_C + U_L = \dfrac{Q_0}{2C}$$

と求められます。

次に，時刻 $t$ の場合の系のエネルギーを求めてみます。静電エネルギーおよび磁気エネルギーは，それぞれ

$$\begin{aligned} U_C &= \dfrac{Q(t)^2}{2C} \\ &= \dfrac{Q_0}{2C} \cos^2 {\omega t} \end{aligned}$$

$$\begin{aligned} U_L &= \dfrac{1}{2} L I(t)^2 \\ &= \dfrac{1}{2} L \omega^2 Q_0^2 \sin^2{\omega t} \\ &= \dfrac{Q_0}{2C} \sin^2 {\omega t} \end{aligned}$$

これより，系の全エネルギーは

$$\begin{aligned} U_{tot} (t) &= U_C + U_L \\ &= \dfrac{Q_0}{2C} (\cos^2 {\omega t} + \sin^2 {\omega t}) \\ &= \dfrac{Q_0}{2C} = U_{tot} (0) \end{aligned}$$

よって，エネルギー保存則が成り立っていることがわかります。