気柱の振動と共鳴現象｜固有振動数や開口端補正の解説

気柱の振動とは，下の図に示すような筒の片端に音叉を近づけると，特徴的な空気の振動が筒の中に現れる現象のことです。 百聞は一見にしかず！ということで，気柱の振動を皆さんに体験してもらいましょう。お手元にある紙を丸めて，耳元に当ててみてください。すると「ボゥーー」というような音が時々聞こえるのが分かると思います。(外で実験するとよりわかりやすいかもしれません。)これは，空気が紙筒の中で共鳴を起こして，特定の管内波長の振動のみが大きな振動としてみなさんの耳に音として伝わっているのです。

詳しくは別の記事で解説しますが，共鳴現象というのは異なる振動数の波同士が重なることで強め合ったり弱めあったりして，結局特定の振動数(固有振動数)をもつ波のみが振動として現れる現象のことです。よって気柱の振動においても固有振動数を求めるというのが，現象を理解するための1つのポイントとなってきます。

今までの議論の流れは，弦の振動の場合と非常によく似ています。それもそのはずで，弦の振動の場合も，気柱の振動の場合も，共鳴現象が重要なテーマになっています。
弦の振動については，以下の記事で詳しく解説しています。
弦の基本振動・固有振動の解説｜線密度と張力で決まる弦の波の速さの導出 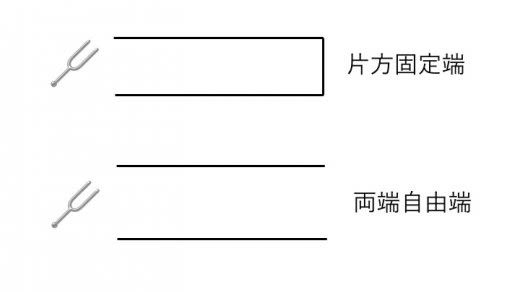具体的に固有振動数を求めていく前に，気柱の振動でも重要になってくる，自由端と，固定端といった概念を復習しましょう。

自由端とは，波が反射する時に波を「自由」に動けるようにしている端，すなわち反射によって波に影響がないような端を意味しており，自由端で反射した波は位相のずれが生じません。

一方，固定端は波を「固定」する端であり，固定端では常に波の変位が0になります。よって入射波と反射波の和が0になるので，固定端で反射した波は逆位相になります。

気柱の振動の場合，上の図のように閉じた端が固定端，開いた端が自由端になっています。先ほど紹介した紙筒は両端自由端の気柱ということになります。

固定端と自由端は，以下の記事で詳しく解説されています。
入射波と反射波（固定端反射・自由端反射）

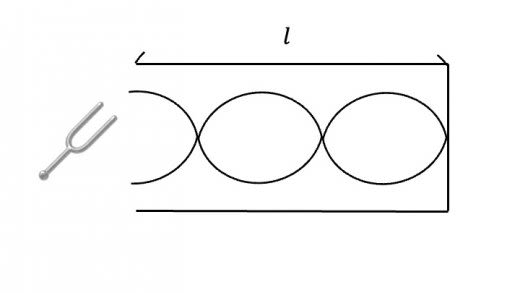気柱内での空気の振動をわかりやすくするために，上のような模式図がよく使われます。これは，気柱内にあたかも「弦の定常波」が存在しているような表現であり，固定端と自由端での波の振る舞いや，気柱の中の波数をわかりやすく表現しています。例えば，上の図では，固定端では節，自由端では腹となることが表現されています。また，図の横波の振幅が大きいところは，縦方向の振幅が大きいことを示しているます。

よく，気柱内での空気の振動は実際にこのような形になっているという勘違いがみられますが，そうではありません。空気の振動は縦波なので，このように横波で表現されるものではありません。よってこの表現は，あくまで模式的であるということに気をつけてください。

以下では，いよいよ気柱の固有振動数を求めていきましょう。
まず前提として，固有振動とはざっくり言えば境界条件を満たす正弦波です。よって今，片方固定端の気柱を考えると，最も長い波長の振動(基準振動)は下のようになります。 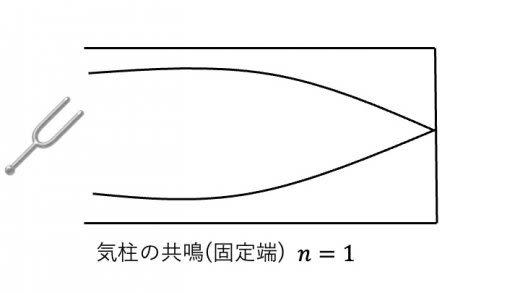次に波長の長い固有振動(3倍，5倍振動)は下の図のようなものです。 基準振動のn倍の振動数の固有振動のことをn倍振動というのでした。 よく観察してみると，片端が固定端の場合，nはどれも奇数になっています。また，n倍振動の場合，気柱の中には $\dfrac{1}{4}$ 波長が $n$ コ入っていることがわかります。(n=1,3,5の時に確かめてみてください。)

よって管の長さを $l$ ，n倍振動の波長を $\lambda$ とすると， $$\dfrac{1}{4}\lambda\times n=l$$ が成り立ちます。よって固有波長はこれを解いて $\lambda=\dfrac{4l}{n}$，固有振動数は音速を $V$ とすると，$f=\dfrac{n}{4l}V$ ということがわかります。 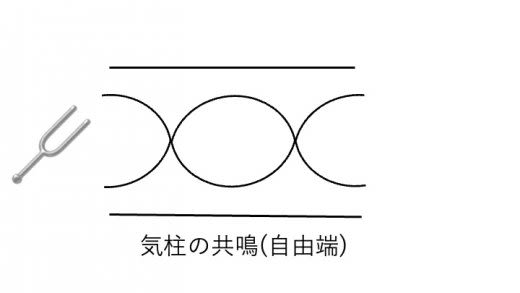両端自由端の時にも固有振動数を求めてみましょう。両端自由端の場合，今度はn倍振動はnが偶数の時しか存在しないことがわかります。(上の図は $n=2$ の場合です。)このことを踏まえて，観察してみると，気柱の中に $\dfrac{1}{4}$ 波長が $2n$ 個入っていることがわかります。よって先ほどと同様に $$\dfrac{1}{4}\lambda\times 2n=l\\ \therefore\lambda=\dfrac{2l}{n},f=\dfrac{n}{2l}V$$ がわかりました。

今までの解説では，気柱の端が暗黙のうちに振動の自由端と等しいと仮定して議論してきました。本来，振動の自由端というのは，そこでの圧力が大気圧と一致するところです。(その位置で振動が真に「自由」になります。)実際は，圧力が大気圧と一致する地点は，気柱の端から気柱の半径の0.6〜0.8倍ほどずれることが知られています。このずれを開口端補正と言います。したがって，今までの議論では開口端補正を無視して議論してきたことになりますが，正確には考慮に入れなければなりません。次の例題を通して開口端反射の議論の方法を学んでいきましょう！

この問題から分かるように，共鳴位置を測定することで得られた値だけで，音速の値を計算できることがわかります。これは音速の測定方法の1つとして知られています。