半導体・ダイオードの電気抵抗と整流作用
半導体の1つであるダイオードは,他の素子とは異なる独自の性質を持っています。高校物理では,回路内におけるダイオードの役割を理解することが重要になってきます。
この記事ではダイオードの電気抵抗や整流作用について解説していきます。また,例題を通じて回路内でのはたらきを理解していきましょう。
半導体の電気抵抗
半導体の電気抵抗
半導体とは
高校物理で扱う物質は,大きく導体・半導体・絶縁体の3つに分類されます。
導体は最も電流を流しやすい物質です。(導体については,導体内における電場・電位 も併せてご覧ください。)他方,絶縁体は,電流をほとんど流さない物質です。
半導体とは,電流の流れやすさが導体と絶縁体の中間程度の物質のことを指します。
電流の流れやすさを評価する値に,抵抗率があります。導体の抵抗率は 程度,絶縁体の抵抗率は 程度となっていますが,半導体の抵抗率は 程度となっています。
半導体の電気抵抗と熱
半導体と導体とを区別する特徴として,電気抵抗と熱との関係があります。
導体は,温度が上がるにつれて電気抵抗も大きくなります。つまり,温度が大きいほど電流を通しにくくなります。
一方,半導体は,ある温度までは絶縁体と同程度の電気抵抗を有しますが,ある温度を境に急激に電気抵抗が小さくなるという特徴があります。つまり,温度が大きいほど電流を通しやすくなるというわけです。
温度に対する電気抵抗の振る舞いが,導体と半導体とで真逆になっている点に注意してください。
半導体の種類
半導体のうち,不純物を含まないものを真性半導体と呼びます。代表的なものには,ケイ素(Si),ゲルマニウム(Ge),セレン(Se)などがあります。
一方,少量の不純物を含むものを不純物半導体と呼びます。真性半導体に比べて電流を通しやすくなっています。不純物半導体は,含まれている不純物の種類に応じて,さらにn型・p型の2種類に分類されます。
n型・p型半導体
ここでは,ケイ素に不純物を混ぜることを考えます。 ケイ素は,価電子を4つ持っています。
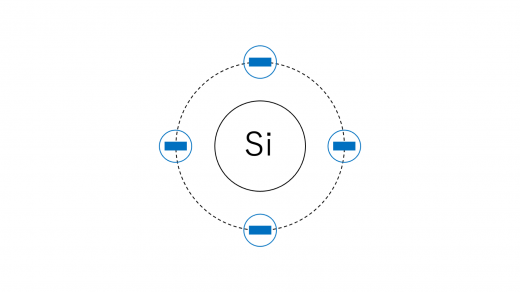
まず,不純物としてリン§やヒ素(As)を加えることを考えます。これらの原子は価電子を5つ持っています。このため,半導体全体としてみると,価電子が余るということになります。
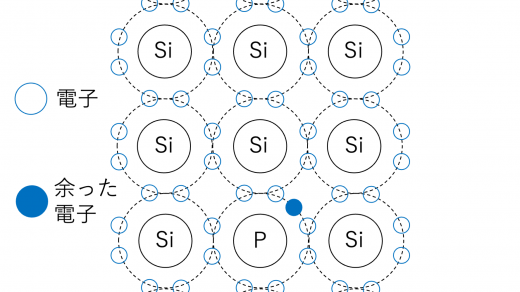
この余った価電子は金属における自由電子のようにはたらくことができ,結果として電流をより通しやすくなります。このような半導体をn型半導体と呼んでいます。
次に,不純物としてホウ素(B)やアルミニウム(Al)を加えることを考えます。これらの原子は価電子が3つしかないので,半導体全体では価電子の数が減少し,結果として正孔(ホール)が発生します。
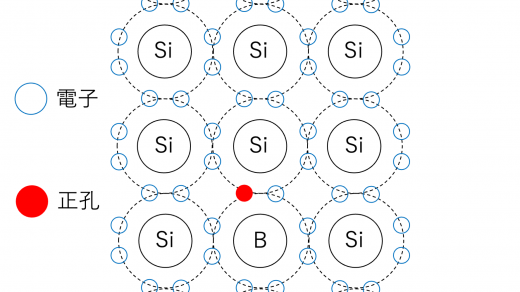
この正孔は正の電荷を持つ粒子としてはたらき,かつ自由に半導体内を動くことができるので,結果としてより電流を通しやすくなるというわけです。このような半導体をp型半導体と呼んでいます
n型半導体における電子やp型半導体における正孔のように,電流を担う粒子をキャリアと呼ぶことがあります。
ダイオードとは
ダイオードとは
ダイオードは,半導体の一種であり,ある一方向にのみ電流を流し,回路内での電流の逆流を防ぐ役割を持っている素子です。
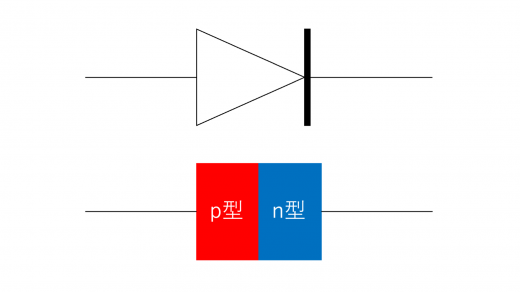
ダイオードは,回路内では,例えば下図のように表されます。
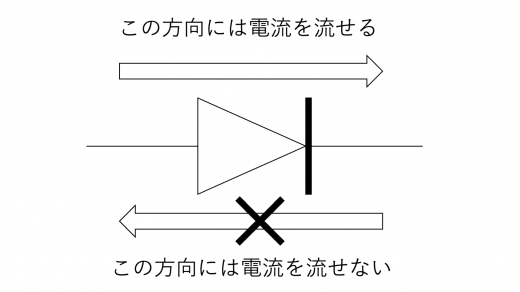
上図の場合,図の左から右へ電流を流すことができますが,右から左へ電流を流すことはできません。
この記事に関連するQ&A
ダイオードのはたらき
ダイオードのはたらき
ダイオードの整流作用
上述したように,ダイオードはある一方向にのみ電流を流すという役割を持っています。これを整流作用などと呼びます。この仕組みについて考えてみましょう。
ダイオードは基本的に,pn接合と呼ばれる構造を持っています。このダイオードは,下図のように,p型半導体とn型半導体を組み合わせて構成されています。図ではp型半導体とn型半導体を,それぞれ「p型」「n型」と略称しています。
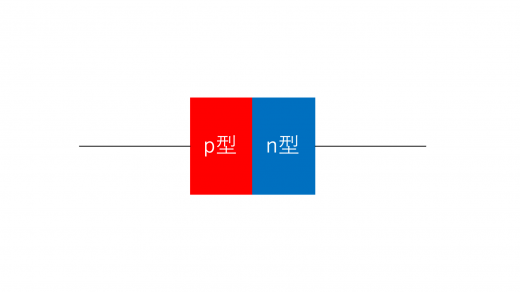
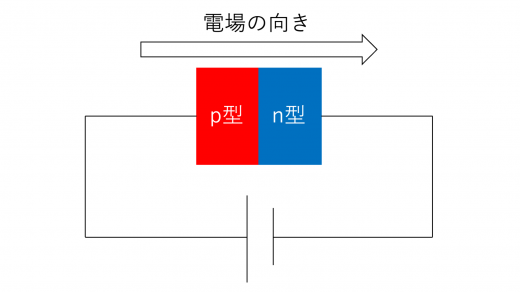
このpn接合を持つダイオードに,電圧を加えてみることを考えます。まず,p型半導体側の方が電圧が高くなるように加えることを考えます。
このとき,p型半導体側では,正孔に電場が加わることで,正孔が半導体の接合面に向かって動きます。一方,n型半導体も,電場から力を受けた電子が移動し,半導体の接合面に向かって動きます。接合面では正孔と電子が結合して安定化します。(正孔とは,本来あるはずの価電子がないことにより生じていたことを思い出してください)
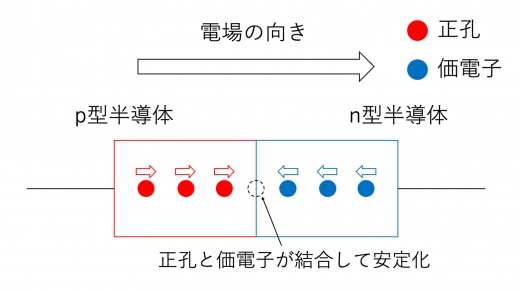
このはたらきにより,電池から供給された負の電荷が,停滞することなく,素子全体での内部を図の右側から左側に移動していると考えることができます。すなわち,電流が図の左側から右側に流れていると考えることができます。
次に,n型半導体側の方が電圧が高くなるように電圧を加えることを考えます。
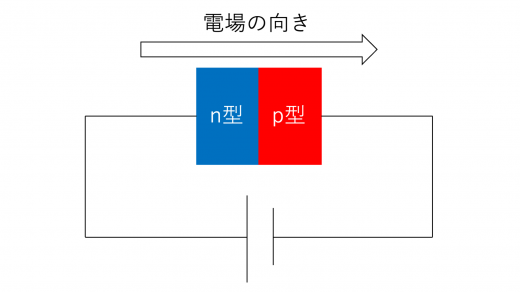
このとき,p型半導体側では,電場から力を受けた正孔が,素子の先端側に向かって運動します。一方,n型半導体側でも,電場から力を受けた電子が,素子の先端側に向かって移動します。
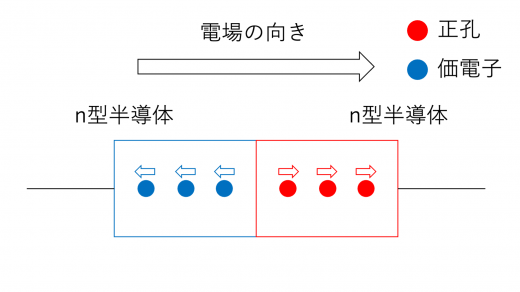
この結果,素子内に荷電粒子が停滞してしまい,電源から供給される電子が素子全体を流れることができにくくなってしまうため,素子に電流が流れなくなってしまいます。
これより,pn接合により作られたダイオードは,p型半導体側の電圧を高く,n型半導体側の電圧を低くすることで電流を流すが,電圧の向きを逆にすると電流を流さなくなることがわかります。
荷電粒子が電場から受ける力の向きについては,電場・磁場・電荷密度・電流密度|電磁気学における基本的な物理量,静電気力とクーロンの法則 も併せてご覧ください。
ダイオードの電気抵抗
高校物理では,ダイオードの電気抵抗は以下の2種類が考えられます。
- 順方向では抵抗を0とみなしてよい
- 順方向での抵抗は,I-Vグラフなどで与えられる。
まず 1. の場合は特に問題がありません。2. の場合は,ダイオードの電気抵抗がグラフで与えられることが多いので,非オーム抵抗の場合(非オーム抵抗とその解法)と同様に解けばよいです。
どちらの場合でも,ダイオードの整流作用には常に注意してください。
例題
例題
例題を通じてダイオードの回路内での扱いに慣れておきましょう。
例題1
以下のような回路を考える。
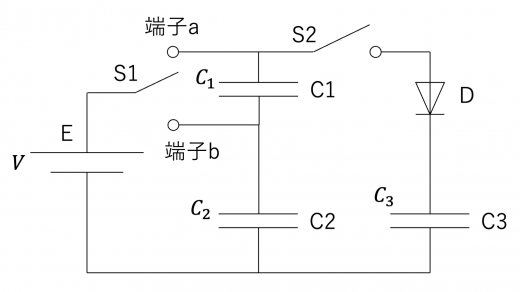
Eは電源を表し,その電圧は とする。また,コンデンサーC1,C2,C3の電気容量はそれぞれ とする。 上図のダイオードDは順方向にのみ電流を流し,そのときの抵抗値は0とみなしてよい。
まず,スイッチS1を端子aに接続し,スイッチS2は開けておく。
(1)定常状態になったとき,コンデンサー1,2が蓄えている電荷の大きさを求めよ。
次に,スイッチS2は開けたまま,スイッチS1を端子bに接続する。
(2)定常状態になったとき,コンデンサー2が蓄えている電荷の大きさを求めよ。また,(1)から(2)に移るまでに電池がした仕事を求めよ。
次に,スイッチS1を開けて,その後スイッチS2を接続する。これ以降, として回答せよ。
(3)定常状態になったとき,コンデンサー3が蓄えている電荷の大きさを求めよ。また,このときコンデンサー3が持つエネルギーが最大となるような を求めよ。
コンデンサーの基本公式等については,コンデンサーの理論 なども併せてご覧ください。
(1)考えるべき回路は以下のようになります。
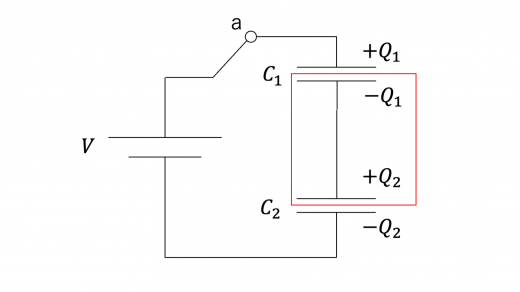
コンデンサー1,2が蓄えている電荷をそれぞれ とします。このとき,キルヒホッフ第二法則(キルヒホッフの法則の解説と例題)より
図の赤線の枠内で,電荷量保存則(電荷と電気量保存の法則)より
以上より
と求められます。
(2)考えるべき回路は以下のようになります。
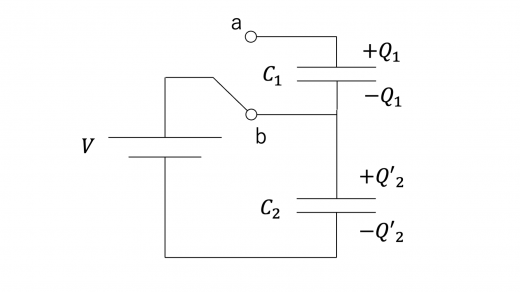
キルヒホッフ第二法則より
コンデンサー1が蓄えた電荷量は変わっていないので,これまでに電荷がした仕事 は
のように求められます。
(3)考えるべき回路は下図のようになります。左の回路がスイッチをつなぎかえた直後,右の回路が定常状態を表しています。
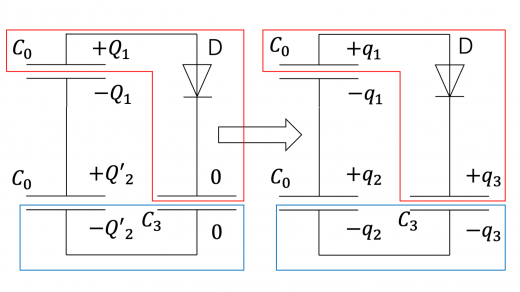
いま,ダイオードの順方向を電荷が通過し,最終的に定常状態に達したとします。このとき となっています。
キルヒホッフ第二法則より
図の赤実線・青実線内での電荷量保存則より
これらより, について解くと
これより,ダイオードには正しい方向に電流が流れたことがわかります。
このとき,コンデンサー3が蓄えている静電エネルギー を求めていきます。
とおき,この関数の増減について調べます。
これより,
これより, は で最大値を取ります。したがって, が最大値となるのは
のときとなります。
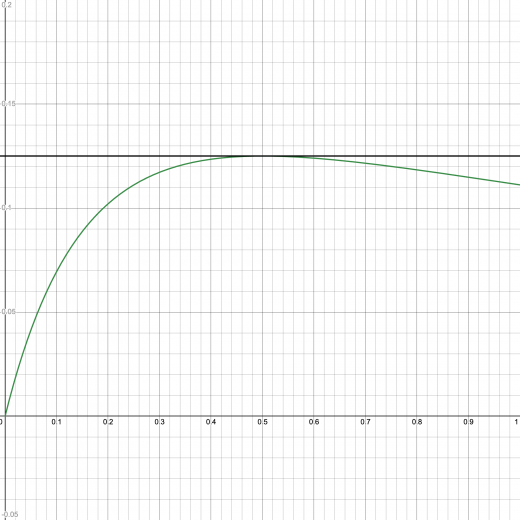
*(補足) は以下の緑実線のようになります。黒実線は を表しています。
例題2
以下で考えるダイオードDは,順方向のみに電流を流す。また,ダイオードDに加わっている電圧と電流の関係は,以下のグラフのように与えられる。
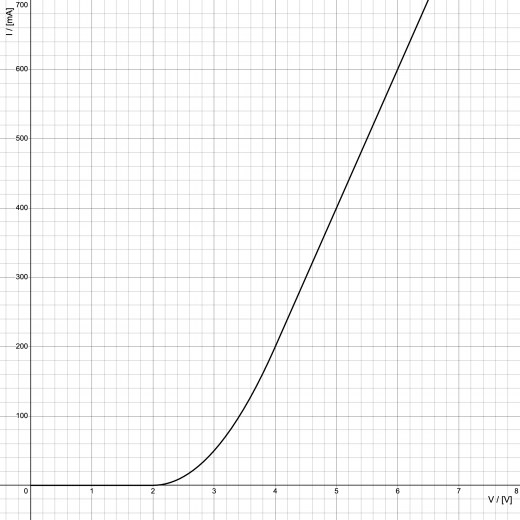
下図のような回路を考える。
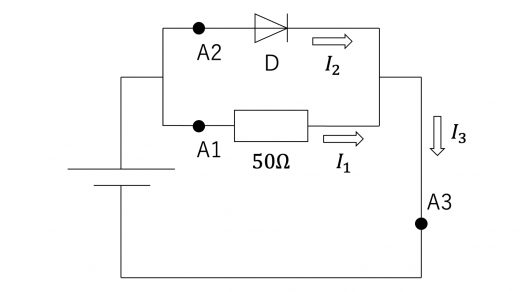
このとき,回路の点A1,A2,A3を流れる電流 をダイオードに加わっている電圧の関数として,同じグラフにプロットせよ。
ダイオードの電気抵抗を考えるのが必要になってきます。
ダイオードに加わる電圧を とおきます。このとき,キルフホッフの第2法則より,抵抗R1に加わる電圧も となります。したがって,点A1に流れる電流 は,単位に注意して
また, のグラフは,与えられているものをそのまま書けばよいです。
さらに,キルヒホッフの第1法則より,点A3に流れる電流 は
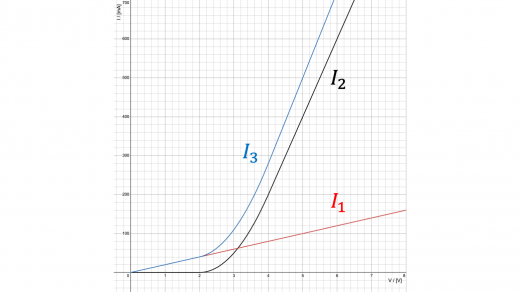
と書くことができます。したがって,グラフとしては, と のグラフを足し合わせたものを書けばよいです。それぞれを同じ平面上に図示すると,例えば下図のようになります。 では のグラフと のグラフが重なっています。
ダイオードは扱いが少々煩雑なので,例題を通じて理解しておくのがおすすめです。










