非オーム抵抗とその解法
高校物理で登場する抵抗のうち,非オーム抵抗について解説します。また,例題を通じて,非オーム抵抗を含む回路の解き方を確認します。
この記事に関連するQ&A
【復習】通常の抵抗
【復習】通常の抵抗
まず,通常の抵抗について確認します。通常の抵抗 (抵抗値 ) は,オームの法則と抵抗の性質 で導出したように,以下の(☆)式で示されるオームの法則を満たしています。
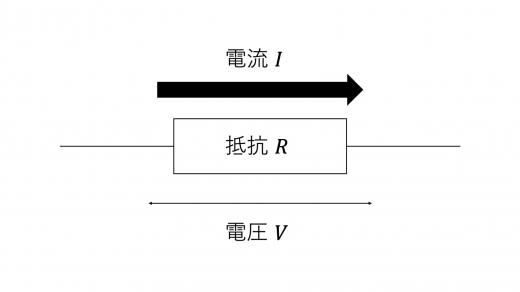
ここで, はそれぞれ,抵抗に加わる電圧,抵抗に流れる電流を表しています。この関係式は,抵抗に加わる電圧と流れる電流との間に比例の関係が成立していることを示しています。
非オーム抵抗とは
非オーム抵抗とは
非オーム抵抗は,非線形抵抗や非直線抵抗とも呼ばれます。その名前からわかるように,非オーム抵抗は,加わる電圧と流れる電流との間に比例の関係が成立しないような抵抗を指しています。
非オーム抵抗は,回路中では以下のような図で表されることが多いです。
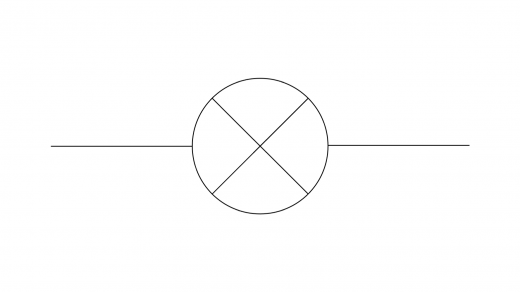
非オーム抵抗に加わる電圧と流れる電流との関係は,問題中に図で与えられることが多いです。
例題
例題
例題を通して,非オーム抵抗を含む回路の解き方を確認しましょう。
電流と電圧の関係が下図のように与えられる非オーム抵抗がある。以下の問いに答えよ。
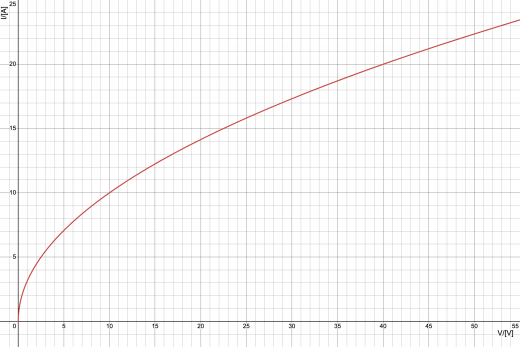
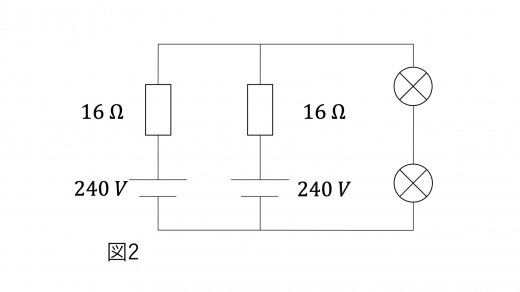
(1)図1のようにように回路を構成したとき,非オーム抵抗に流れる電流の大きさ を答えよ。
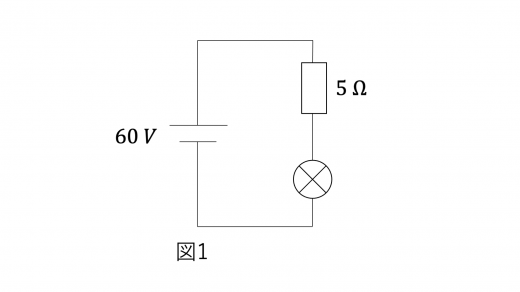
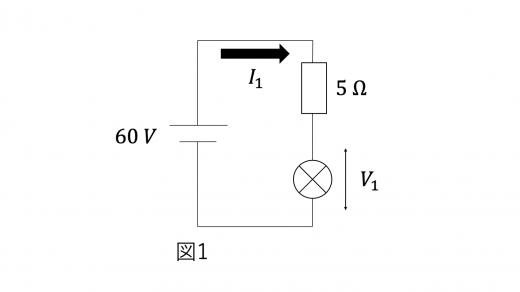
(2)図2のように回路を構成したとき,非オーム抵抗に流れる電流の大きさ を求めよ。
非オーム抵抗を含む回路の問題の基本的な解き方は以下の通りです。
-
非オーム抵抗に流れる電流と加わる電圧を文字でおく。
-
キルヒホッフの第1・第2法則 (詳しくは キルヒホッフの法則の解説と例題 を参照) を用いてそれらの間の関係式(*)を求める。
-
与えられた非オーム抵抗の電流と電圧の関係のグラフに,(*)式のグラフを書き込んで,交点を求める。(グラフの軸に注意!)
(1)回路に流れる電流を ,非オーム抵抗に加わる電圧を とする。このとき,非オーム抵抗に流れる電流も となる。
キルヒホッフ第2法則より
(1)式を与えられたグラフに書き込む。
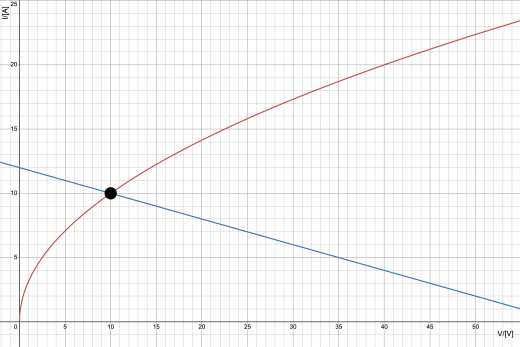
グラフの赤実線が与えられた非オーム抵抗のふるまいのグラフ,青実線が(1)式のグラフである。
交点は上図の黒点が示す通り, と求められる。(1)式の単位に注意して,求める電流は 。
(2)回路に流れる電流を下図のように とおく。回路内の2つの非オーム抵抗には同じ大きさの電流が流れるため,2つの非オーム抵抗に加わる電圧も等しい。その電圧を とおく。
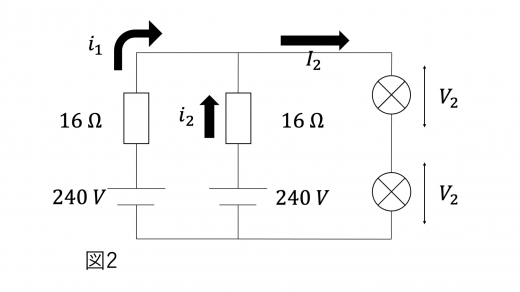
まず,キルヒホッフの第1法則より,回路を流れる電流について
が成り立つ。
また,回路内の電圧の関係について,キルヒホッフの第2法則より
(2-2)・(2-3)式を足し合わせて
(2-4)式を与えられたグラフに書き込む。
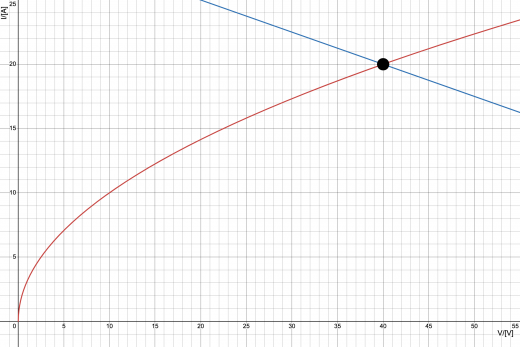
グラフの赤実線が与えられた非オーム抵抗のふるまいのグラフ,青実線が(2-4)式のグラフである。
交点は上図の黒点が示す通り, と求められる。(2-4)式の単位に注意して,求める電流 は 。
非オーム抵抗の問題は,そこまでパターンがある問題ではありません。典型問題をしっかりと解けるようにしておきましょう。











