古典論から量子論へ:黒体輻射(放射)

更新 2023/10/24

高校物理と大学物理とをつなげるテーマをいくつか取り上げ解説します。今回は，古典論と量子力学とをつなげる黒体輻射(放射)について解説します。

黒体輻射とは

熱輻射(放射)・黒体とは**熱輻射(放射)**とは，物体が熱せられた時に電磁波が発せられる現象のことです。例えば，鉄などの金属が熱せられているときに，赤や橙色のように見えることがありますが，これは鉄からその色の波長帯の光が出ているためです。
また，黒体とは，光を全て吸収し，全く反射しないような理想的な物体のことです。
実験的事実上述したように鉄の例で考えてみましょう。鉄は，温度を上げていくにつれて，赤，黄，白の順に色が変化することが知られています。このように，物体の熱輻射は，熱せられているときの温度によって変化します。
実験により，物体の熱輻射により生じる電磁波の振動数と強度の関係(スペクトル分布)は下図のような概形になることがわかっていました。
上図より，温度が高くなるほど，スペクトル(エネルギーの強度を表す単位)の強度が大きくなることがわかります。また，スペクトルがピークとなる振動数が，温度が高くなるにつれて大きくなっていることもわかります。これは，温度が高くなるにつれて，物体が発する色が変化することを表しています。

この問題の(1)番のDHを求める問題で、三角形DMAを切り出して、直線AMに垂直になるように、DHを降ろしていますが、 2

2022年慶応志木の問題です。大問▪️3の(2)番で、このような問題がありました。ここで図を書くと、添付図のようにな 3

問あなたの今の気持ちを伝える文を書こう。という問題に下記の様に答えを書きました。 ●Im glad that giv 4

エタノール（C2H5OH）の量論比での酸化反応式と理論空燃比を求めよ A) 化学反応式 B) 理論空燃比 5

古典論の範囲内での説明

古典論の範囲で黒体輻射を説明しようと試みた公式を二つ紹介します。
なお，この章で登場するグラフは，簡単のため，定数および温度 TTT を 111 として描いています。
ウィーンの公式それまでの研究により，熱平衡状態にある黒体輻射の，ある振動数におけるスペクトルの強度は，温度 TTT のみの関数として表されることが知られていました。
実験事実に合うように発明された公式として，ウィーンの公式があります。
振動数 ν\nuν におけるスペクトル強度を U(ν)U(\nu)U(ν) とすると
U(ν)=Aν3exp⁡(−BνT)
U(\nu) = A {\nu}^{3} \exp{\left(- \dfrac{B \nu}{T} \right)} 
U(ν)=Aν3exp(−TBν​)
ただし，A,BA, BA,B は実験から決まる定数です。
ウィーンの公式をグラフで表すと下図のようになります。
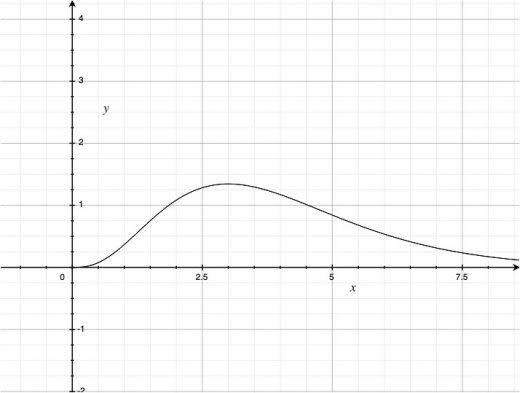
ウィーンの公式は，高振動数帯では実験結果をよく説明しますが，低振動数帯では実験結果をうまく説明することができませんでした。
レイリー・ジーンズの公式一方，古典論から理論的に導かれた公式として，レイリー・ジーンズの公式があります。
U(ν)=8πc3ν2kBT
U(\nu) = \dfrac{8 \pi}{c^3} {\nu}^{2} k_B T
U(ν)=c38π​ν2kB​T
ここで，ccc は光速，kBk_BkB​ はボルツマン定数を表します。
グラフで表すと下図のようになります。
レイリー・ジーンズの公式は低振動数帯の実験結果とよい精度で一致していることがわかりました。しかし，高振動数帯の実験結果を説明することはできませんでした。
結局，古典論の範囲では，全ての振動数帯の実験結果を再現する理論曲線は見つかりませんでした。

プランクの公式と光の粒子性

プランクの公式とはウィーンの公式とレイリー・ジーンズの公式を結びつけようという考察を経て，プランクという学者がプランクの公式を見出しました。初めに紹介した実験結果は，以下の公式により全ての振動数帯をよく説明できます。
U(ν)=8πc3hν3exp⁡(hνkBT)−1
U(\nu) = \dfrac{8 \pi}{c^3} \dfrac{h {\nu}^{3}}{\exp{\left( \dfrac{h \nu}{k_B T} \right)}-1}
U(ν)=c38π​exp(kB​Thν​)−1hν3​
ここで，hhh はプランク定数と呼ばれる定数です。
プランクの公式は，低振動数帯ではレイリー・ジーンズの公式を，高振動数帯ではウィーンの公式を再現します(補足にて解説)。
光の粒子性プランクがこの公式に対する理論的説明を考える上で注目したのが，実験事実ではスペクトル強度に限界があるという点です。この事実は古典論の範囲内では説明ができないものですが，プランクは「光(電磁波)のとりうるエネルギーは hνh \nuhν の整数倍となる」と考えることにより，プランクの公式の理論的説明を可能としました。赤字のような考えをプランクの量子仮説と呼びます。
プランクの量子仮説は，整数 nnn と光のエネルギー EnE_nEn​ を用いて以下のように表すことができます。
En=nhν
E_n = n h \nu
En​=nhν
これは，光が取りうるエネルギーは，hνh \nuhν という量を一括りとして，数えられる量として考えられる，すなわち光には粒子性があるということを示唆しています。
この考えを発展させて，アインシュタインが光量子仮説を提唱することになります。こちらは別の記事にて解説予定です。

【補足】プランクの公式の式変形

プランクの公式が，低振動数帯ではレイリー・ジーンズの公式を，高振動数帯ではウィーンの公式を再現することを示します。

証明

ほぼ等しいということを表す記号として， $\sim$ を用いる。

まず，振動数が小さいとき，つまり $h \nu \ll k_B T$ のときを考える。 $\dfrac{h \nu}{k_B T} \ll 1$ であるから， $\left(\dfrac{h \nu}{k_B T} \right)$ の２次以降の量は無視できる。テイラー展開(e^xのマクローリン展開，三角関数との関係)により

$\exp{\left(\dfrac{h \nu}{k_B T}\right)} \sim 1 + \dfrac{h \nu}{k_B T}$

プランクの公式に代入して

$U(\nu) \sim \dfrac{8 \pi}{c^{3}} \dfrac{h {\nu}^{3}}{1 + h \nu/k_B T -1} \\ = \dfrac{8 \pi}{c^{3}} \dfrac{h {\nu}^{3}}{h \nu/k_B T} \\ = \dfrac{8 \pi}{c^{3}} {\nu}^{2} k_B T$

これはレイリー・ジーンズの公式と一致している。

次に，振動数が大きいとき，つまり $h \nu \gg k_B T$ のときを考える。 $\dfrac{h \nu}{k_B T} \gg 1$ であるから， $\exp{\left(\dfrac{h \nu}{k_B T} \right)} \gg 1$ と考えてよい。したがって

$\exp{\left(\dfrac{h \nu}{k_B T} \right)} -1 \sim \exp{\left(\dfrac{h \nu}{k_B T} \right)}$

ゆえに，プランクの公式より

$U(\nu) \sim \dfrac{8 \pi}{c^{3}} \dfrac{h {\nu}^{3}}{\exp{\left(\dfrac{h \nu}{k_B T} \right)}} \\ = \dfrac{8 \pi h}{c^{3}} {\nu}^{3} \exp{\left(-\dfrac{h \nu}{k_B T} \right)}$

$\dfrac{8 \pi h}{c^{3}}, \dfrac{h}{k_B}$ はそれぞれ定数であるから，それぞれ $a,b$ とおけば，これはウィーンの公式と一致する。

(注)上の証明では $h \nu$ と $k_B T$ の大きさを比較しました。どちらも，典型的なエネルギースケールとして，大学物理では重要な値です。

光の粒子性の概念は非常に重要です。