斜面に置かれた物体の問題:保存則の利用
この記事では,斜面の上に物体が載っているタイプの問題を扱います。この問題は大学入試で頻出なので,基本的な考え方を理解して,よく練習しておく必要があります。
この記事に関連するQ&A
物体にはたらく力
物体にはたらく力
 斜面に物体が載っているタイプの問題とは,上のような図でしばしば与えられます。物体にはたらく主な力は,重力と垂直抗力です。またこれらに加えて,応用問題になると,その他に,摩擦力やばねの弾性力が現れます。
斜面に物体が載っているタイプの問題とは,上のような図でしばしば与えられます。物体にはたらく主な力は,重力と垂直抗力です。またこれらに加えて,応用問題になると,その他に,摩擦力やばねの弾性力が現れます。
 まず重力と垂直抗力について考えてみましょう。物体の運動を考えるときに定石となるのが,斜面に沿う方向と斜面に垂直な方向に力を分解して考えることです。つまり,上の図のようになります。
まず重力と垂直抗力について考えてみましょう。物体の運動を考えるときに定石となるのが,斜面に沿う方向と斜面に垂直な方向に力を分解して考えることです。つまり,上の図のようになります。
重力を各成分に分解する際にポイントとなるのが,斜面の角度 です。多くの問題でこの斜面の角度 は初めから与えられており,簡単な三角形の相似を図中で考えると,重力と斜面の垂直方向のなす角度が図のように となることがわかります。よって重力を各成分に分解することができます。
実は斜面の角度 は摩擦がある斜面の問題で,より重要な役割を果たします。静止摩擦係数 の斜面を考えるとき,物体を斜面に置いて滑り落ちない条件は で表されます。ここで等号が成立する ,すなわち を満たす を摩擦角といいます。
摩擦角に関しては,以下の記事で詳しく説明してあるので,興味がある方はご覧ください。
摩擦力の定義|動摩擦力・静止摩擦力・摩擦係数の解説
摩擦角の定義|摩擦角の求め方と例題
では,いよいよ実際に問題を解いてみて,斜面と物体の問題について理解を深めましょう!
斜面と物体の問題1
斜面と物体の問題1
まず最初に最も基本的な問題です。
以下の図のようになめらかな斜面上に質量 の物体を置いた。以下のように 軸をとり, で物体は にあったとする。
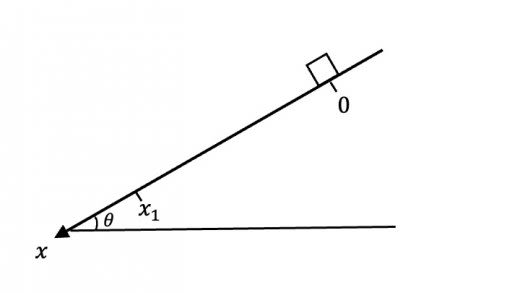 (1)物体にはたらく垂直抗力 を求めよ。
(1)物体にはたらく垂直抗力 を求めよ。
(2)物体が に到達する時刻 を求めよ。
(3)物体が に到達したとき,物体の速さ を求めよ。
<解答>
(1)まず,素直に物体の運動方程式を,斜面に平行な方向と垂直な方向に分けて立ててみましょう。物体にはたらく重力をどのように分解するかは,既に上で解説しました。
水平方向:
垂直方向:
垂直抗力の運動方程式から,(1)の答えは となることがわかります。
(2)続いて水平方向の運動方程式を解きましょう。すると がわかります。これに を代入することで となります。
(3) なので,これに(2)で求めた を代入すると, となります。
別解
この問題では,運動方程式を立てて加速度を積分して解いても,大した手間はかかりませんでしたが,もっと複雑な系になるとこの方針では大変です。よって運動量と力積の関係や,力学的エネルギー保存を用いて解くのがむしろ賢い方針になります。実際,(3)は力学的エネルギー保存より, が成り立つので,これを用いて瞬時に答えがわかります。
また,(2)も運動量と力積の関係 (斜面方向の重力による力積を考える。)と力学的エネルギー保存により求めた を用いて解くことができます。
斜面と物体の問題2
斜面と物体の問題2
続いて,摩擦がある問題です。前問の別解と同様に,各保存量に着目すると簡単に解けます。
 (大まかな設定は前問に従う)斜面が, は動摩擦係数 の粗い斜面となっている。 で の状態から物体が斜面に沿ってすべりだし, で の地点で静止した。 と を求めよ。
(大まかな設定は前問に従う)斜面が, は動摩擦係数 の粗い斜面となっている。 で の状態から物体が斜面に沿ってすべりだし, で の地点で静止した。 と を求めよ。
<解答>
まず物体が に到達する時刻 と 速度 は,前問の結果よりわかっています。 を境に,物体には摩擦力が加わりはじめます。
運動量と力積の関係及び運動エネルギー変化と仕事の関係を用います。 と 間での運動量と力積の関係は これより がわかります。
一方 と 間での運動エネルギー変化と仕事の関係は となります。よって
以上の方針から分かるように, と 間で保存則を考えると,どちらの時刻においても物体の速さは なので,運動量や運動エネルギーが になって計算が楽になります。このように,ただ計算するだけでなく,どの方針が一番計算が楽になるかを常に考えられるようになるといいですね!
斜面に物体が置かれた問題は,基本的ですがバラエティに富んでいて,差がつく問題だと思います。問題に応じて適切な方針が立てられるように訓練しましょう。











