摩擦角の定義|摩擦角の求め方と例題
この記事では,摩擦角について解説します。まず,摩擦角の定義を述べた後,摩擦角を用いて解くことができる例題を紹介します。
摩擦角の定義と求め方
摩擦角の定義と求め方
斜面に物体が静止している以下の図のような系を考えます。このとき,物体にはたらく抗力と,重力が逆向き同じ大きさでつりあっています。

ここで,斜面の角度 を徐々に大きくしていくとどうなるでしょうか? ある角度 を超えると,摩擦の力が負けて,物体は徐々に下に滑り始めるはずです。物体が滑り始める条件を,斜面の角度で表すことにします。
静止摩擦力を ,静止摩擦係数を ,垂直抗力を と書くと,物体が滑り始めない条件を以下のように表すことができます。 ここで物体が滑り始めるその瞬間に,摩擦力が最大摩擦力となり,不等式の等号が成立します。滑り始める瞬間の斜面の角度は を満たします。この のことを摩擦角といいます。具体的に書くと, となります。
摩擦力や摩擦力に関する用語については,以下の記事をご覧ください。
摩擦角は,斜面の性質のみによる定数 (静止摩擦係数)のみによります。斜面に置いた物体の質量にはよらないことに注意してください。
摩擦角の例題
摩擦角の例題
以下では,具体的な計算を通して摩擦角の概念に慣れていきましょう。
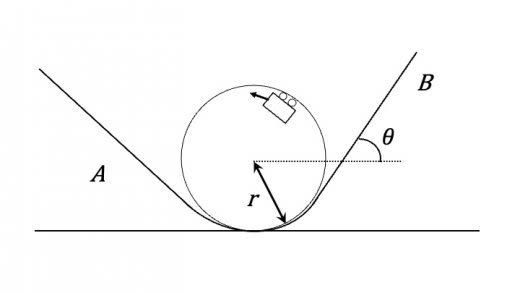
以下のような,半径 の円形で,途中で宙返りするジェットコースターがある。ジェットコースターのレール上を,図に示した質量 のトロッコが走る。左側の斜面レール(Aとする)には摩擦はなく,右側の斜面レール(Bとする)には高さ より上のレールに摩擦があるとする。傾斜角 は,動摩擦係数 を用いて,となるように設定されている。レールとトロッコの間には,固定などはないとする。
(1)レールAで静止していたトロッコが出発した。円形レールの最下点を最初に通過した時のトロッコの速さは だった。円形レールでトロッコが離れずに1回転するための の条件を求めよ。
(2)(1)の条件が成り立っている時,トロッコは円形レールを1回転後,レールBを進んだ。その後トロッコはレールBで最高点に達した。最高点到達後,トロッコの振る舞いを述べよ。
(1)まず,トロッコが円形レールから離れないために が満たすべき条件を考える。
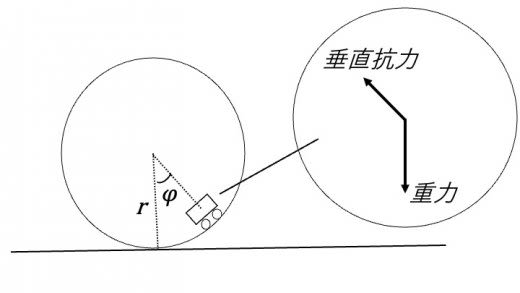 トロッコの運動方程式とエネルギー収支を考える。円形レールの最下点でのトロッコの速さを ,図に示した,角度 でのトロッコの速さを とすると,
トロッコの運動方程式とエネルギー収支を考える。円形レールの最下点でのトロッコの速さを ,図に示した,角度 でのトロッコの速さを とすると,
接戦方向:
向心方向:
エネルギー収支:
となる。向心方向の式と、エネルギー収支及び,円運動の関係式 より, の時を考えると, となる条件は,
次に,トロッコが地上からの高さ の地点に到達する条件を考える。エネルギー保存の式から, となる。以上より求める条件は,
(2)摩擦角を とすると,定義より静止摩擦係数を用いて, となる。一方,動摩擦係数は,最大摩擦係数より小さいことが知られている。(上記の摩擦についての記事参照)よって 以上より,最高点に到達した後,トロッコは静止する。
摩擦角を知っているだけで解けてしまう問題もたまに大学入試で出題されます。











