初期の原子模型から量子論のボーアモデルまでの道のり

1897年にJ.J.トムソン(英, 1856-1940)が電子の存在を明らかにしました。

→比電荷の測定と電子の発見

電子が発見されたことで, 当時の科学者は「電子が原子内にどのような状態で, どこに配置しているのか」という疑問に頭を悩ませました。原子は電荷を持たないため, 電子を打ち消し合う正の電荷も原子内に存在しているはずです。その正の電荷と電子（負の電荷）の位置関係は大きな謎でした。

初期の原子模型はいくつか考えられましたが, この記事では以下の２つを紹介します。

1. J.J. トムソンのブドウパン型

2. 長岡半太郎の土星型

上記以外にもモデルはありましたが, この２つは対照的なモデルとして教科書でよく取り上げられます。

トムソンのブドウパン型の原子模型

電子の存在を明らかにしたトムソンは大きな正の電荷のかたまりの中に電子が埋まっている原子モデルを考えました。

これはブドウパン型モデルといわれ, 正の電荷のかたまりをパン, 電子を粒状のブドウに見立てています。ブドウパン型は英語で plum pudding model といいます。

トムソンは, 電子は正の電荷の中を運動すると考えました。

このブドウパン型モデルは, 後にラザフォードが行ったα線の実験で, 原子核の存在が明らかになったことで破綻します。この実験については後述します。

長岡半太郎の土星型の原子模型

日本の物理学の基礎を築いた長岡半太郎(長崎県生まれ, 1865-1950)は正の電荷を中心として, 電子が外側を輪を成して回転している原子モデルを考えました。これは土星型モデルといわれています。

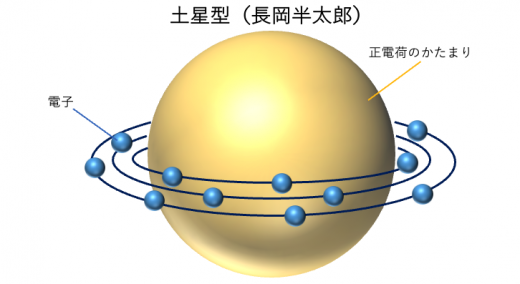
この原子模型は現在のボーアモデルと少し似ていますが, 電子が軌道運動しているのがポイントです。土星型モデルは大きな欠陥があったため, 当時の科学者にはあまり支持されなかったそうです。

土星型モデルの難点

土星型モデルの難点は, 電子の特性にあります。電磁気学では, 電子は回転運動すると電磁波(光)を放出する性質があります。

土星型モデルのように電子が回転運動を続けると, 電磁波を発生し続け, 電子が持つエネルギーが減少していきます。

すると, 電子はらせん軌道を描きながら中心の正の電荷に向かっていき, 最後には中心に帰着することが考えられました。

実際の原子は光を放出し続けることも, 中心に接近することもありません。 この欠陥が指摘されたため, 土星型モデルでは原子モデルとして浸透しませんでした。

1909年にラザフォードがα線を用いた実験を行い, 原子の中心に正の電荷が集中している原子核の存在を提唱しました。これによりブドウパン型モデルが否定され, 新たにラザフォード(ニュージーランド, 1871-1937)が考案した原子モデルが登場しました。

α線を用いたラザフォードの実験

ラザフォードの実験は, 金属箔にα線を当て, その後α線がどう進むかを観察します。α線はウランなどの放射性物質から出る放射線の一種で, α線の正体は, 正の電荷を持つ「α粒子」の流れです。すなわち, α線は電気的にプラスの性質を持ちます。

ラザフォードは下図（左）のような, α線を金属箔に照射する装置を組みました。金属箔は蛍光板に覆われています。α粒子は蛍光板に当たると発光するため, α線の到達地点を観測できます。これにより, α線の軌跡をたどることができます。

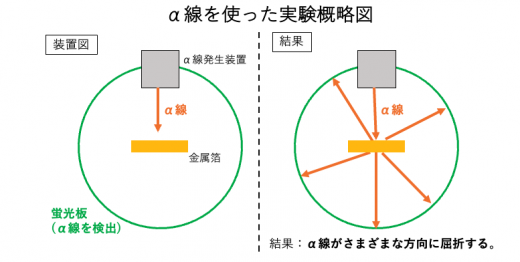
実験の結果は右図に示すように, 直進するα線, 屈折するα線, 入射方向に跳ね返るα線が観測されました。

ブドウパン型モデル（トムソン）の否定

ラザフォードの実験結果から, 原子模型の考察をしていきます。

仮に原子がトムソンが提案したブドウパン型モデルである場合, 上記の実験を行えばα線はすべて直進すると考えられます。

ブドウパン型モデルの場合, 原子内全体に広がるプラスの電気と, 点在するマイナスの電気が打ち消し合います。そのため, 原子内に電荷の偏りがなく, 電気的に中性になります。

プラスの性質を持つアルファ粒子が通過しても, 原子に影響されず直進すると考えられました。

しかし, 実験ではα線の軌道が変わったことから, ブドウパン型の原子モデルでは辻褄が合わないことが証明されました。

ラザフォードモデルの登場

ラザフォードは, α線がさまざまな方向に屈折した実験結果から, 「原子の中心にプラスの電気が集中している」と考えました。電子はプラスの電荷から距離を置いて, 回っています。

原子の中心に集中してプラスの電荷があるため, 原子中心付近が電場が強くなります。プラスの声質を持つα線が原子の中心付近を通過すれば, 電気的反発によりα線の進路が曲げられます。

このような原子モデルを考えると, α線の軌道が変わった実験結果の説明がつきます。ラザフォードが考えた, 原子の中心のプラスの電荷のかたまりは皆さんも知っての通り「原子核」のことです。

ラザフォードは原子核を中心とした, 太陽系のような原子模型を提案しました。これをラザフォードモデルといいます。このとき, まだ中性子は発見されていませんが, ラザフォードは中性子の存在を予測しています。

ここで違和感を覚えたかもしれませんが, ラザフォードのモデルは電子の状態に関してあまり言及されておらず, 長岡半太郎の土星型モデルと同じ問題点を残したままなのです。

土星型モデルは,

• 電子が電磁波を出し, 次第にエネルギーを失い, 中心に接近する問題

を抱えていました。これを解決したのが, デンマークの物理学者ニールス・ボーアです。ボーアモデルまであと一歩です。

ニールス・ボーア（デンマーク, 1885-1962）は, ラザフォードの原子模型をベースに, ド・ブロイが提案した電子の二重性の考えを取り入れることで, ボーアモデルを提案しました。

ボーアモデルの話の前に, ド・ブロイ波長のおさらいから始めます。

ド・ブロイ波長（ド・ブロイ方程式）

ド・ブロイ（仏, 1892-1987）は1923年に, 電子の波長と運動量の関係式であるド・ブロイ波長（ド・ブロイ方程式）を示しました。詳しくは以下の記事を参考にしてください。

→ドブロイ波長

ド・ブロイ波長の発見によって, 電子が粒子性と波動性の二面性を持つ物質であることが示されました。

量子論的な水素原子模型（ボーアモデル）

ボーアが考案したモデルは, ラザフォードモデルにド・ブロイの電子の量子性を融合させた「量子論的な水素原子模型」というものです。簡単に, ボーアモデルとも呼ばれます。

• "量子論的な"とは, この原子模型は古典力学では証明できない, 量子力学に基づく電子の二重性を踏まえた考え方だからです。

• なぜ"水素原子模型"なのかというと, 水素原子の構造は電子一つと陽子一つの最も単純なモデルで考えやすいからです。

※量子論は複雑で, 水素原子以降の原子に関する厳密な解明は未だできていません。

電子は波として存在する

「量子論的な水素原子模型」を理解する上で重要なポイントは3つあります。

1. 電子は円軌道で回転する粒子ではなく, 波として存在する。

2. 「電子が持つ波長の整数倍 ＝ 電子軌道の円周の長さ」

3. 電子が軌道間を移るにはジャンプするしかない。

上記について詳しく解説していきます。

ボーアモデルでは, 電子は回転運動している粒子ではなく, 波として存在していると考えます。これは図で表しにくく, イメージしにくいと思うので, こういうものだと受け入れると良いと思います。

電子が存在する波は, 中途半端な波は作れず, 波長の整数倍の長さの波になります。したがって, 電子が存在できる軌道は「円周＝波長の1倍」, 「円周＝波長の2倍」, 「円周＝波長の3倍」… と円周の長さは飛び飛びに大きくなっていきます。

中途半端な波を作らないというのは, 例えば「円周=波長の3.5倍」になるような波は存在しないということです。

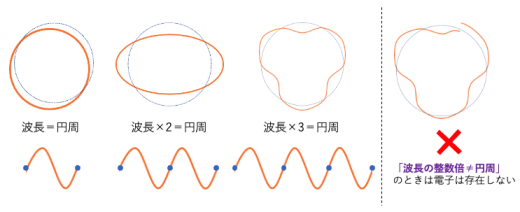
ここで重要なのは電子が存在できる波はとびとびだということです。外側の軌道ほどエネルギー準位が高くなります。最も内側のエネルギーが低い軌道を「基底状態」といいます。

基底状態の電子が外からやってきた光子を吸収することがあります。すると, 電子が持つエネルギーが大きくなり, 一定のエネルギーに達すると, 次の軌道にジャンプします。この状態を「励起状態」といいます。

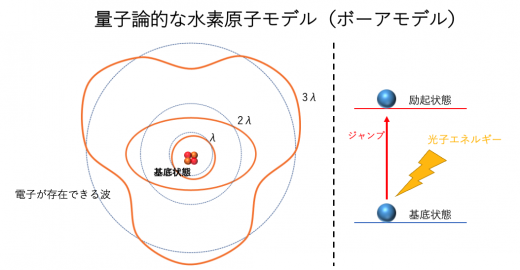
これがボーアが考案した「量子論的な水素原子模型」です。ボーアモデルは図で表現しにくく, イメージがしづらいかと思いますが, 以下のポイントを抑えるようにしましょう。

1. 電子は円軌道で回転する粒子ではなく, 波として存在する。

2. 「電子が持つ波長の整数倍 ＝ 電子軌道の円周の長さ」

3. 電子が軌道間を移るにはジャンプするしかない。

ボーアの量子条件

ボーアモデルの「電子が持つ波長の整数倍＝ 電子軌道の円周の長さ」ということを深ぼっていきます。これを数式で表現してみます。

電子の円軌道の半径 $r$ とすると, 円周の長さは $2\pi r$ となります。

「円周の長さ＝波長 $\lambda$ の $n$ 倍」となるため,

$$2 \pi r = n \lambda$$

が成り立ちます。ド・ブロイ波長 $\lambda = \dfrac{h}{m_e v}$ を用いると,

$$\begin{aligned} 2 \pi r &= n \dfrac{h}{m_ev} \\ m_e vr &= n \dfrac{h}{2\pi} \\ \end{aligned}$$

この式はボーアの量子条件と呼ばれています。

この式を用いたボーアが打ち立てた量子論は, 前期量子論と呼ばれます。前期量子論には, プランクの黒体反射の理論やプランク定数, アインシュタインの光量子仮説（光電効果）などが含まれます。

ちなみに, 後期量子論とはハイゼンベルグの行列力学や, シュレディンガー方程式などを指します。

ラザフォードモデルの欠点は解消したのか？

ボーアモデルについて学んだところで, 長岡半太郎の土星型モデルやラザフォードモデルで指摘された

• 電子が電磁波を出し, 次第にエネルギーを失い, 中心に接近する問題

をボーアモデルがクリアできているのかを考えていきます。

この問題は電子が古典力学に基づき, 粒子として円運動をしていると考えてたために生じた問題です。

しかし, ボーアモデルでは電子を量子力学に基づいて波として考えるため, この問題は起きません。ボーアモデルの電子は軌道ごとに固有のエネルギーを持つため, 電子が連続的にエネルギーを失うことはありません。

ボーアモデルから量子力学の発展へ

ボーアは量子力学の考え方を用いて, 理論的な原子模型である「量子的な水素原子模型」を完成させました。

さらに同年代に, 実験で水素原子が発するスペクトルをプリズムで分光し, その波長がボーアの理論と一致したことから, ボーアの量子条件を裏付ける結果となりました。

しかし, 当時は量子力学の黎明期であるため, 電子がとびとびのエネルギーを持つことなどに対する批判も多かったようです。「これを理論物理とするなら, 私は物理学をやめる。」と主張する物理学者もいたようです。

ここから, 量子力学の急速に発展に伴い, ボーアの原子模型は受け入れられていきます。