第一宇宙速度・第二宇宙速度・脱出速度

更新 2021/04/27

「第一宇宙速度」，何かロマンを感じる言葉ですよね。この記事では，第一宇宙速度とは何か，また第一宇宙速度を一般化した概念として，「脱出速度」を紹介します。宇宙工学での応用についても紹介します。

第一宇宙速度とは何か

簡単な思考実験突然ですが，簡単な思考実験をしてみましょう。
あなたは公園で友人とキャッチボールをしています。相手が取りやすい位置，つまり胸の位置を目掛けてボールを投げることを考えてみましょう。ゆっくりボールを投げると，ボールは相手に届く前に地面に落ちてしまいますが，速く投げると相手に届けられますね。
この時ボールの軌道はどのようになっているでしょうか。放物運動ですから，正確には放物線を描きますが，ボールを速く投げるとき，その軌道はほぼ直線的になります。
プロ野球を思い浮かべてみてください。
こちらは大谷翔平投手が165kmをマークした時の動画です。
大谷投手が速球を捕手に目掛けて投げるとき，その軌道は放物線というよりは直線に見えますよね。
つまり，ここで分かるのは，
「モノを速く投げれば投げるほど，その軌道は直線的になる」
ということです。
では，軌道がほぼ直線に見えるような速度でボールを投げながら，キャッチボールする2人の距離をどんどん離していきましょう。そうすると，ボールの軌道は，徐々に地球に沿った円軌道に近づきませんか。
これを実現するような速さこそが，のちに述べる第一宇宙速度です。
しかし，そうは言っても所詮は思考実験。そのようなことが本当に実現するのでしょうか。
この定性的な考察が正しいことを，定量的な考察で示してみましょう。
定性的考察から正しいと思われること
ある速さ以上で投げた速さは，地球を一周して，自分のところに戻ってくる。
証明の前に，万有引力について簡単に復習しておきましょう。天体レベルの質量の物体の寄与を考慮して運動を考えるとき，以下の公式で表される万有引力が無視できなくなります。
万有引力の公式
質量 M，mM，mM，m の2質点の間には，万有引力が働く。2点の距離を rrr とするとき，万有引力の大きさは
F=GMmr2
F = G \dfrac{Mm}{r^2}
F=Gr2Mm​
万有引力を考えるとき，重力を考慮する必要はなくなります。
実は，重力は地表付近での万有引力を近似的に表したものだからです。地球の半径に対し，地表での私たちの世界の高さは十分低く，万有引力はほぼ一定に見えます。万有引力としてではなく，重力として扱う方が物理系を表すのに楽なのでそう表しているのです。
重力とは万有引力のことなのですから，
mg=GMmR2
mg = G \dfrac{Mm}{R^2}
mg=GR2Mm​
という式が成立します。これを変形すれば，次のようなことが導けます。
万有引力定数の変換の公式
gR2=GM
g R^2 = GM
gR2=GM
このことを用いて，上述の「定性的考察から正しいと思われること」を証明しましょう。
証明
ボールの質量を mmm，ボールを投げる人の身長を hhh，地球の質量を MMM，地球の半径を RRR，万有引力定数を GGG とする。
ボールが万有引力の影響で地球の周りを円運動しているとき，その速度を v1(>0)v_1 (>0)v1​(>0) とすると，運動方程式より
m　v2R+h=GMm(R+h)2(1)
m　\dfrac{v^2}{R+h} = G \dfrac{Mm}{(R+h)^2} \tag{1}
m　R+hv2​=G(R+h)2Mm​(1)
ここで，hhh は RRR に比べて十分小さいとして良いので，
R+h∼R(2)
R+h \sim R \tag{2}
R+h∼R(2)
が成り立つ。
(1)， (2)式より，
v1=GMR
v_1 = \sqrt{\dfrac{GM}{R}}
v1​=RGM​​
ここで，前述の公式より，
GM=gR2
GM = g R^2
GM=gR2
これを代入して，
v1=gR
v_1 = \sqrt{gR}
v1​=gR​
すなわち，gR\sqrt{gR}gR​ でボールを投げれば，ボールは地表付近を円運動する。
第一宇宙速度の定義第一宇宙速度の定義とは
「人工衛星が地表付近を円運動し続けるために必要な速度」
です。すなわち，先にボールの考察から求めた v1=gRv_1 = \sqrt{gR}v1​=gR​ こそが，第一宇宙速度であったわけです。

第n宇宙速度と脱出速度

「第n宇宙速度」と呼ばれるものは，他にも
第二宇宙速度
第三宇宙速度
などがあります。
また，これらに似たような概念として，
脱出速度
があります。順に解説していきます。
第二宇宙速度第二宇宙速度とは，「物体が地球の引力を振り切って運動するために必要な速度」のことです。
第二宇宙速度を求める前に，万有引力による位置エネルギーについて復習しておきます。万有引力による位置エネルギーは以下のような公式で表されます。
万有引力による位置エネルギーの公式
U=−GMmr
U = -G \dfrac{Mm}{r}
U=−GrMm​
これを証明してみます。
証明
質量が M，mM， mM，m である2つの物体A，Bの間に働く万有引力は，距離が rrr であるとき，先に述べたように
F=GMmr2
F = G \dfrac{Mm}{r^2}
F=Gr2Mm​
今，物体Bを，基準点 r0r_0r0​ から，万有引力と大きさが等しく逆向きの外力 fexf_{ex}fex​ を加えながら，ゆっくりと位置 rrr まで動かすことを考える。保存力の定義より，この時した仕事が万有引力による位置エネルギーとなる（保存力や位置エネルギーの定義については位置エネルギーの定義と例（重力・弾性力・クーロン力）を参照）。AによるBに対する万有引力は，BA⃗\vec {BA}BA の向きに働くことに注意して，その値 U(r0)U(r_0)U(r0​) は，
U(r0)=∫r0r(fex)dr′=∫r0rGMmr2dr′
\begin{aligned}
U(r_0) = \int^{r}_{r_0} (f_{ex}) dr^{\prime} \\
= \int^{r}_{r_0} G \dfrac{Mm}{r^2} dr^{\prime} \\
\end{aligned}
U(r0​)=∫r0​r​(fex​)dr′=∫r0​r​Gr2Mm​dr′​
∴U=[−GMmr]r0r=GMmr0−GMmr
\therefore U = \left[-G \dfrac{Mm}{r} \right]^{r}_{r_0} = G \dfrac{Mm}{r_0} - G \dfrac{Mm}{r}
∴U=[−GrMm​]r0​r​=Gr0​Mm​−GrMm​
基準点は任意にとって良いが，計算が簡単になるよう，r0→∞r_0 \to \inftyr0​→∞ とすることが多い。その時の U(r0)U(r_0)U(r0​) を改めて UUU と表記すると，
U=−GMmr
U = -G \dfrac{Mm}{r}
U=−GrMm​
となる。
この公式で注意すべきなのは，
「マイナスがつくかどうか」
です。これを確認する方法として，「定性的に考察する」をお勧めします。
万有引力の場合，2つの物体を遠ざけた後，手を離すとどうなるでしょうか。当然，2物体は近づきますよね。つまり，万有引力による効果を考えるとき，「2物体の距離は近い方が安定」というわけです。安定ということは，エネルギーは距離が小さいほど小さい値を取る，ということです。
ここで，下図の反比例のグラフを見てください。
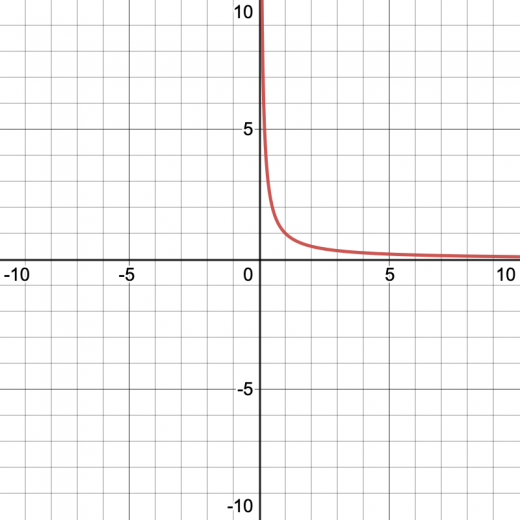
距離が小さいほど小さい値を取るのは，2番目の図，つまり係数が負の値の時ですよね。ですから，万有引力による位置エネルギーにはマイナスがつく，というわけです。
話が大幅に逸れてしまいました。第二宇宙速度の求め方に戻りましょう。
第二宇宙速度の求め方
物体，地球の質量をそれぞれ m，Mm， Mm，M，地球の半径を RRR，第二宇宙速度を v2(>0)v_2 (>0)v2​(>0) とする。この物体を，初速度 v2v_2v2​ で地表から放ることを考える。この時，物体が無限遠まで到達でき，その時速さが0になると考える。
万有引力は保存力であり，今考えている運動では物体は万有引力のみを受けて運動すると考えて良いので，地球の地表と無限遠で力学的エネルギー保存則より
12mv22−GMmR=12m⋅02−0=0
\dfrac{1}{2} m {v_2}^2 - G \dfrac{Mm}{R} = \dfrac{1}{2} m \cdot 0^2 -0 =0
21​mv2​2−GRMm​=21​m⋅02−0=0
∴v2=2GMR
\therefore v_2 = \sqrt{2 \dfrac{GM}{R}}
∴v2​=2RGM​​
万有引力の変換の公式を用いると，
v2=2gR
v_2 = \sqrt{2gR}
v2​=2gR​
となる。■\blacksquare■
第一宇宙速度 v1v_{1}v1​ と第二宇宙速度 v2v_2v2​ の間には，
v2=2v1
v_2 = \sqrt{2} v_{1}
v2​=2​v1​
の関係があります。
第三宇宙速度第三宇宙速度とは，「物体が太陽の引力を振り切って運動するために必要な速度」のことです。
これを求めるには，第二宇宙速度に太陽の物理量を代入して求めれば良いことになります。
脱出速度脱出速度とは，「物体がある天体(系)の引力を振り切って運動するために必要な速度」のことです。
対象とする天体が地球の場合には第二宇宙速度，太陽の場合には第三宇宙速度に当たります。
一般の天体に対しても，先ほど求めた第二宇宙速度の表式に，その天体の質量と半径を代入してやれば，その天体からの脱出速度を求めることができます。

人工衛星への応用

第一宇宙速度が応用上重要になるのは，人工衛星の飛行においてです。

人工衛星を打ち上げる時，地球に戻ってくることがないようにするためには，先に求めた第一宇宙速度以上で打ち上げることが必要になります。

しかし，第二宇宙速度以上になると，その人工衛星は地球の引力圏を抜け出してしまいます。

人工衛星には，「はやぶさ」のように，天体や宇宙の謎を解明することが目的のものもあれば，地図の作成，天気予報，GPSのためのデータの収集が目的のものもあります。各人工衛星の目的に則した軌道を描かせるために，どのような速度で打ち上げるかが調整される必要がありますね。

「宇宙速度」という概念は，自分達とはあまり関係がないように思えますが，実は生活のなかで重要な働きをする身近なものであると言うことができると思います。理論と実践をリンクさせられるのが，物理学の面白さの一つですね。