• 解決済み

    @staroverhead

    2025/9/29 20:02

    1 回答

    回転体の問題です。14.8の(1)なのですが、自分は、x=√2-yとしてy=1からy=-2までをy軸回転した値を求めた後に、図の線で囲まれた部分の円錐を引くことで題意の体積を求めようとしたのですが、解答と値が一致しません。

    この解答の仕方は間違っていますか？

    1. 高校生
    2. 数学
    3. 数学Ⅲ

    ベストアンサー

    ベストアンサー

    @Enigmathematics

    2025/10/5 14:48

    @staroverhead 様の回答の仕方は方針としては全然大丈夫だと思います！解答と違うのであれば計算ミスで合わない、とかでしょうか...？一応その方針での回答(略解)を書いておきますね。




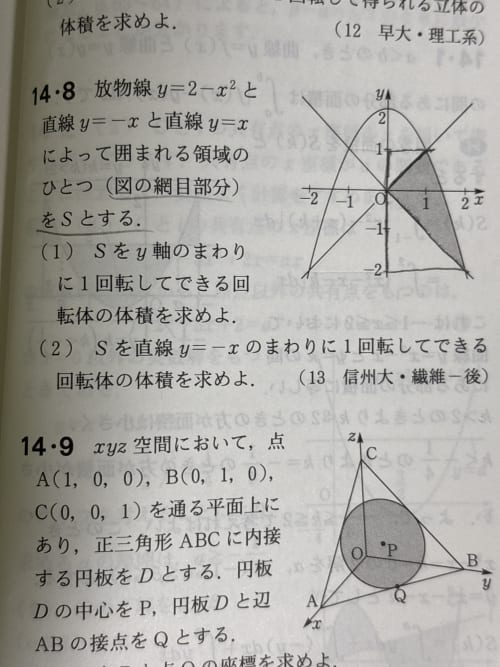
    図で囲まれた円錐の部分のうち、小さいほうをV1V_1、大きいほうをV2V_2とすると、求める体積は、

    V=π∫−21x2dy−V1−V2V=\pi \int_{-2}^{1} x^2 dy-V_1-V_2

    となります。先にV1,V2V_1,V_2を導出して、それぞれ

    V1=π3    V2=8π3V_1=\dfrac{\pi}{3}\ \ \ \ V_2=\dfrac{8\pi}{3}

    あとは、積分を処理しましょう

    V=π∫−21x2dy=π∫−212−y2dy=π∫−21(2−y)dy=π[2y−y22]−21=152π\begin{align*} V&=\pi \int_{-2}^{1} x^2 dy \\&=\pi \int_{-2}^{1} \sqrt{2-y}^2 dy \\&=\pi \int_{-2}^{1} (2-y) dy \\&=\pi \left[2y-\dfrac{y^2}{2}\right]^{1}_{-2} \\&=\dfrac{15}{2} \pi\end{align*}

    よって求める答えは、V=152π−π3−8π3=92πV=\dfrac{15}{2} \pi-\dfrac{\pi}{3}-\dfrac{8\pi}{3}=\dfrac{9}{2}\pi


    もしこの回答があってないということもあるので、模範解答とご自身の回答をお伝えしてくれると助かります。


    補足

    超万が一誤謬等あればご連絡ください


    そのほかの回答（0件）

    関連する質問

    もっとみる