et2をtについて微分すると2tet2より
∫01+h2tet2 dt=[et2]01+h=e(1+h)2−1
となり与式のlogの中身は以下のように変形できる
h→0lim(e−1e(1+h)2−1)h1=h→0lim(1+e−1e(eh(h+2)−1))h1
=h→0lim(1+e−1e(eh(h+2)−1))e(eh(h+2)−1)e−1・h1・e−1e(eh(h+2)−1)
=eh1・e−1e(eh(h+2)−1)となり
与式=limh→0e−1e・heh(h+2)−1、limh→0heh−1=1より
h→0lime−1e・heh(h+2)−1=h→0lime−1e・(h+2)h(h+2)eh(h+2)−1
=e−1e・2・1=e−12e
読みづらくなってしまいすみません。
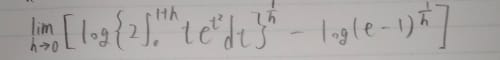
質問者からのお礼コメント
なるほど!理解出来ました!ありがとうございます!