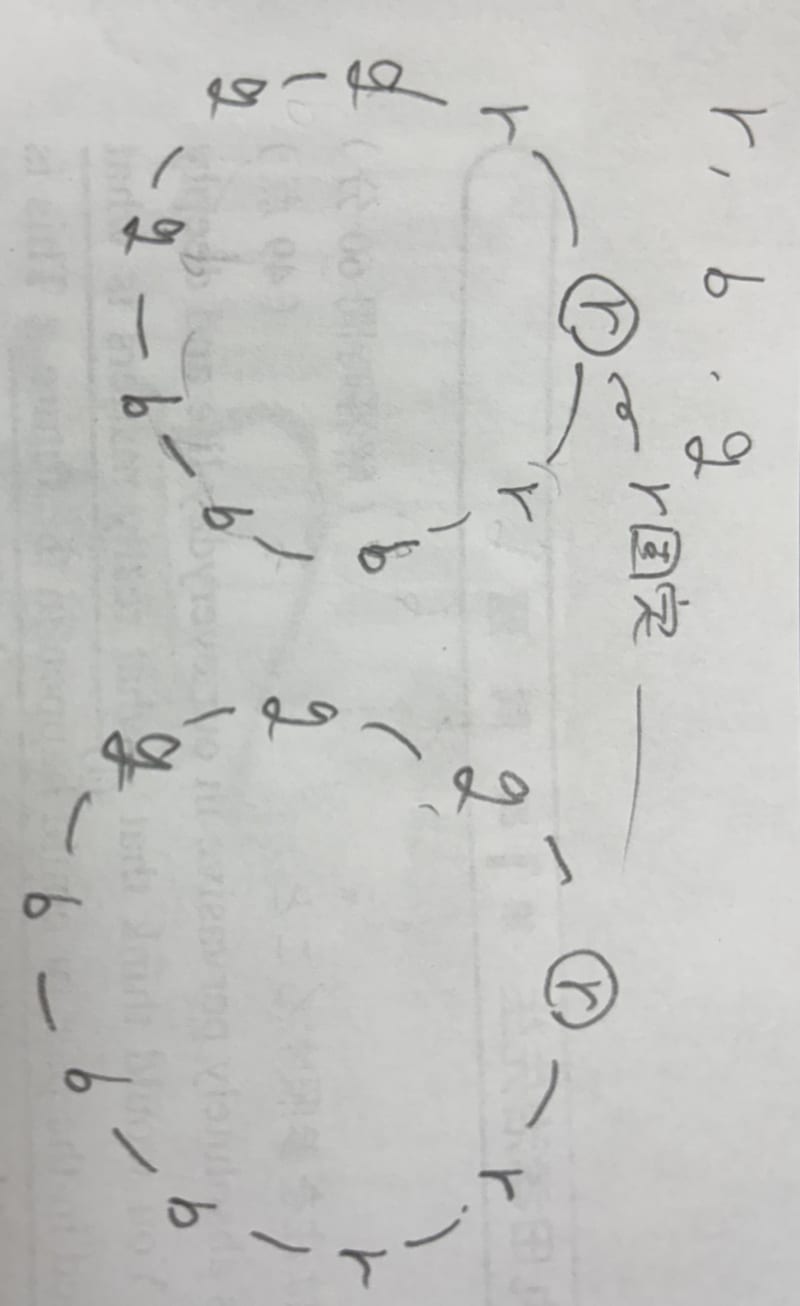
長さ n の順列 X が与えられたとき,X を右へ 0 要素分回転した順列,1 要素分回転した順列,……,n−1 要素分回転した順列の集合を O(X) と書き,X の軌道と呼ぶことにします。また,O(X) の要素数を軌道の長さと呼ぶことします。
(たとえば,X=RBBG ならば,X の軌道は O(X)={RBBG,GRBB,BGRB,BBGR} で,軌道の長さは 4。)
円順列の場合,同じ軌道に含まれる 2 つの順列は同じであると見なされます。
(たとえば BGRB∈O(RBBG) だから,RBBG,BGRB は同じ円順列。)
だから円順列を数え上げることは,順列の軌道を数え上げることに同じです。
いまの問題の場合,赤玉 3 個,青玉 3 個,緑玉 3 個を普通の順列として並べる仕方の数は,
9C3×6C3×3C3=1680。
1680 個のうち,ほとんどの順列は長さ 9 の軌道をもちますが,例外的に長さ 3 の軌道をもつ順列が存在します。次の 6 つです:
RBGRBGRBG, GRBGRBGRB, BGRBGRBGRRGBRGBRGB, BRGBRGBRG, GBRGBRGBR
したがって,赤玉 3 個,青玉 3 個,緑玉 3 個を円順列として並べる仕方の数は,
3(軌道の長さが 3 の順列の個数)+9(軌道の長さが 9 の順列の個数)=36+91680−6=188。
一応計算機で検算してみると,たしかに答えは 188 で,188 個を具体的に書き出すと下の写真のとおりになります。

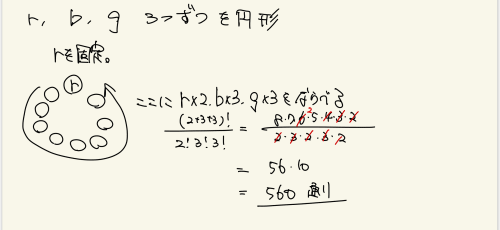









質問者からのお礼コメント
ありがとうございます。完璧にわかりました。具体例があるおかげで理解しやすかったです。