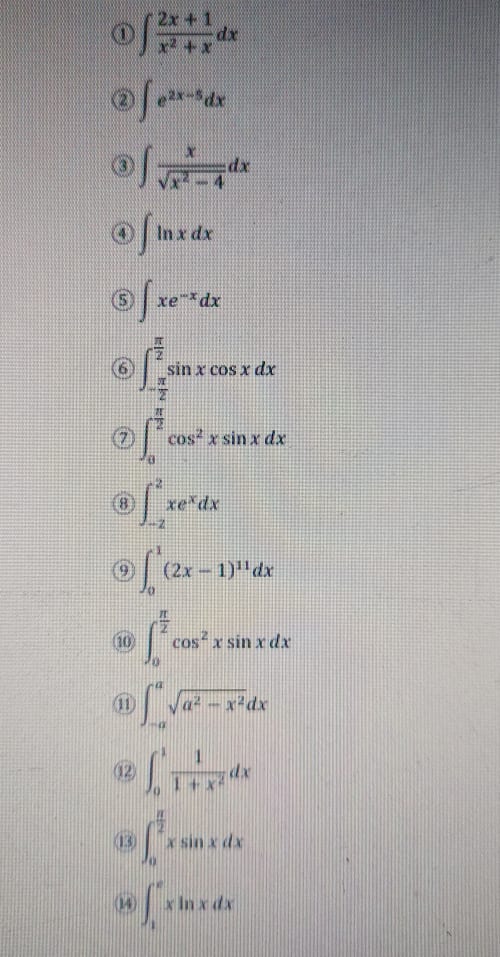どなたか次の積分の問題の過程と解教えて欲しいです🙇🙇🙇🙇

長くなりそうなのでなるべく簡潔に説明しますね。

①これは、$\log$が頭に出てくるかが問題です

$$(与式)=\int \dfrac{(x^2+1)'}{x^2+x} dx=\log (x^2+x)+C$$

対数の微分の時を考えるとイメージできます

②合成関数の積分(微分の逆操作)だけです

　$$\int e^{2x-5} dx= \dfrac{1}{2} e^{2x-5}+C$$

③これは、分母の内部の関数の微分形が分子にある形なので、これも合成関数の微分の要領でイメージ

$$(与式)=\int (\sqrt{x^2-4})' dx= \sqrt{x^2-4}+C$$

因みに、$x^2の2$の部分は、ルートの「二分の一乗」の微分の際におりてくる係数でキャンセルされています。

④ これはもう式ごと覚えてしまいましょう。めちゃ便利です (部分積分法です)

$$(与式)=\int x' \ln x dx=x \ln x-\int x \dfrac{1}{x} dx$$

$$= x \ln x-x+C$$

⑤これも部分積分法で

$$(与式)= x (-e^{-x} )+\int e^{-x} dx=-x e^{-x}-e^{-x}+C$$

⑥これは合成関数の微分を考慮するといいかもしれません

$$(与式)=\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} (\sin x)' \sin x dx$$

$$=\left[ \dfrac{1}{2}(\sin x)^2 \right]_{-\frac{\pi}{2}}^{\frac{\pi}{2}}=0$$

これは、倍角の公式を使ってもいいと思います

⑦これは上記と同様に解いていけば問題なしです。

$$(与式)=\int_{0}^{\frac{\pi}{2}} -(\cos x)' \cos^2 x dx=\left[ -\dfrac{1}{3}(\cos x)^3 \right]_{0}^{\frac{\pi}{2}}=\dfrac{1}{3}$$

⑧またまた部分積分法でいけます

$$(与式)=\biggl[ x e^x \biggr]_{-2}^{2}-\int_{-2}^{2} e^x dx=2 e^2+2e^{-2} -e^2+e^{-2}=e^2+3e^{-2}$$

⑨$11$乗とかいうのに惑わされずに解けば簡単です

$$(与式)=\int_{0}^{1} \{\dfrac{1}{2×12} (2x-1)^{12} \}'dx=\dfrac{1-1}{24}=0$$

⑩ ？⑦番と全く同じ問題のようなので割愛しますね

⑪これは正直、半円をイメージするだけで積分の操作は言っちゃうと必要ないです。　つまり、答えは　$\dfrac{1}{2} \pi a^2$です。

ですが、念のために積分もしておきます。補足として後ほど載せます。

⑫これは定型とも言うべきやつです。$\tan$で置換をして、　

$\tan t=x$とし、$dx=\dfrac{1}{\cos^2 t} dt$

$$(与式)=\int_{0}^{\frac{\pi}{4}} \dfrac{1}{1+\tan^2 t } \dfrac{1}{\cos^2 t} dt=\int_{0}^{\frac{\pi}{4}} dt=\dfrac{\pi}{4}$$

⑬また部分積分法です、$\sin$を先に積分します

$$(与式)=\biggl[ x \cos x \biggr]_{0}^{\frac{\pi}{2}}+\int_{0}^{\frac{\pi}{2}} \cos x dx=1$$

⑭これまた同じく、$x$を先に積分しましょう

$$(与式)=\biggl[ \dfrac{1}{2}x^2 \ln x \biggr]_{1}^{e}-\int_{1}^{e} \dfrac{1}{2}x^2 \dfrac{1}{x} dx=\biggl[ \dfrac{1}{2}x^2 \ln x \biggr]_{1}^{e}-\biggl[ \dfrac{1}{4}x^2 \biggr]_{1}^{e}=\dfrac{1+e^2}{4}$$

これで以上です。冗長になりすみません🙇

また何かあったら返信の欄に載せます、、