という問題では、yを消去して出てくるxの二次方程式が解を持つすなはちDが0以上、として計算しますが、この時xのとりうる範囲-1以上1以下を考慮しなくてもよいのはなぜですか?????
このことを考えると、出てくる2次方程式は、単にDが0以上として計算するだけでは全然ダメで、ちゃんと解の配置問題のように場合分して-1以上1以下にxが解をもつとして計算しないといけないと思ってしまいます。
どうすればいいですか?見識者の方がいればこの本質をご教授いただけると嬉しいです。
下の写真は、京大2015文系の問題をヘタクソに解いた時に出てくる方程式で、このzの存在条件を立式する場面です。僕はこの方程式が、zが0以上2以下で解を持つ条件を求めないといけない、と勘違いしてこの方針を捨てました。
論理記号による理解はしていたため、以前からあんまり気にしていなかったのですが、論理記号使わずに解いていったらわからなくなってしまいました。。。
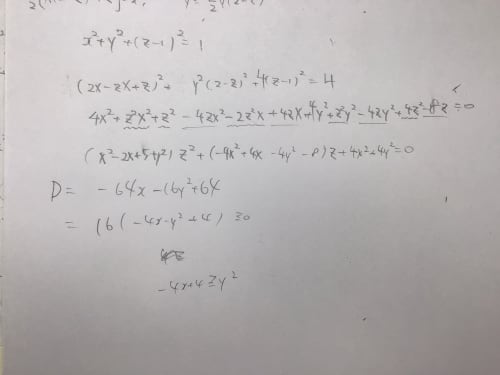
ベストアンサー

削除済みユーザー
を実変数とすると,
を示すには によって を消去すればよく, を示すには とおいて を導入すればよいです。
幾何学的に言えば,左の連立方程式は 空間内に図形 を,右の方程式は 平面内に図形 を定めています。 を消去することは, を 平面へ投影して を得ることにあたります。それは 軸に平行な投影で, 平面へ垂直に影をおとすので, の存在範囲を変えません。だから,左右の方程式が定める の存在範囲は同じです。
つまり, の存在範囲を考えるには右の方程式だけ考えればよいので, のことは忘れることができます。
より一般に,連立方程式からある変数を消去しても残る変数の存在範囲は変わりません。また逆に,新たな変数を導入しても既存の変数の存在範囲は変わりません。それは上に書いたことから推察できると思います。
ありがとうございます。
ちょっと疑問なんですが、
結局は、 という式に、わざわざ というのを入れなくてもいい、ということに帰着しますか?
「左右のxの存在範囲が同じ→右の方程式だけ考える」がつながりません。
例えば最初の式に、 という条件があるとすると、これは解の配置で解く必要があると思うんですが、違いはどう説明できるのですか?
削除済みユーザー
すみません,問題を「 の存在範囲を求めよ」と勘違いしていたので,意味の通じない所があったかと思います。
正しくは「左右で の存在範囲が同じなので,左を考える代わりに右の方程式を考えればよい」と書くべきでした(存在範囲が同じであることの説明は投稿内容のとおりです。)
多分,この訂正で意味が通じるようになったのではないかと思いますが,追加の疑問点があるときはまたお知らせください。
シェアしよう!
そのほかの回答(2件)
の範囲に解をもつような解の配置問題として考えても、もちろん同じ答えが得られます。
具体的には、代入した後の式を とおくと、
となります。つまり、 についての方程式 が の範囲に解をもつための必要十分条件は、
となります。
これらを解いて、結局 が得られます。
いらない理由としては、この式を満たす実数 がの組が存在するときは、必ず の範囲に収まっているからです。だから気にしないで良いということですね。
ちなみに余談ですが、解の配置問題自体はかなり重要です。(判別式・軸・端点の つに注目。判別式と軸は平方完成で一発クリア)
また、円と直線が共有点をもつことと、円の中心と直線の距離が半径以下であることは同値です。円が出てきた場合は、計算量を減らすためにこの解法を用いることから考えてみましょう。
として、
①と②が共有点を持つ
⇔①と②が、同じxに対して、yが同じになる
⇔③が解xを持つ
ここで、
③が解を持つ⇔①と②が共有点を持つ(この時xは-1以上1以下は自明)
という解釈でいいですか?









質問者からのお礼コメント
とてもよく理解できました。文字の存在についてさらに理解が深まりました。