京大実戦ですが、(また積分)なぜ自分の解答で正しい軌跡がでないのかが全くわかりません。かれこれ3時間ぐらい悩んでます(時間無駄にした気がして大損)。
たしかに模範解答のように角度を置くことをやろうと思いましたがどうしても直線の正領域負領域を使って内心を出したかったのでこれで解答してしまい、軌跡は正しく出ません。
なんでなのか全然わかりません。模範解答の軌跡をジオジブラで打ってみると明らかに媒介変数がないと表現出来なさそうなんです。もうわけがわからないです。。。。。
汚い字ですが、何か教えていただけると嬉しいです。


ベストアンサー

点と直線の公式の分母はがつきますね。そこで間違えている気がします。
この問題に対してですが、内心の座標をとおき、与えられた条件を満たすように代数的に解く…というのは悪手だと思います。数学的には正しいですが、同値性を保ったまま式変形をするにはかなり煩雑になります。私も途中で諦めました…。を外すには2乗するしかありませんが、勝手に2乗すると同値性が崩れてしまいますよね。
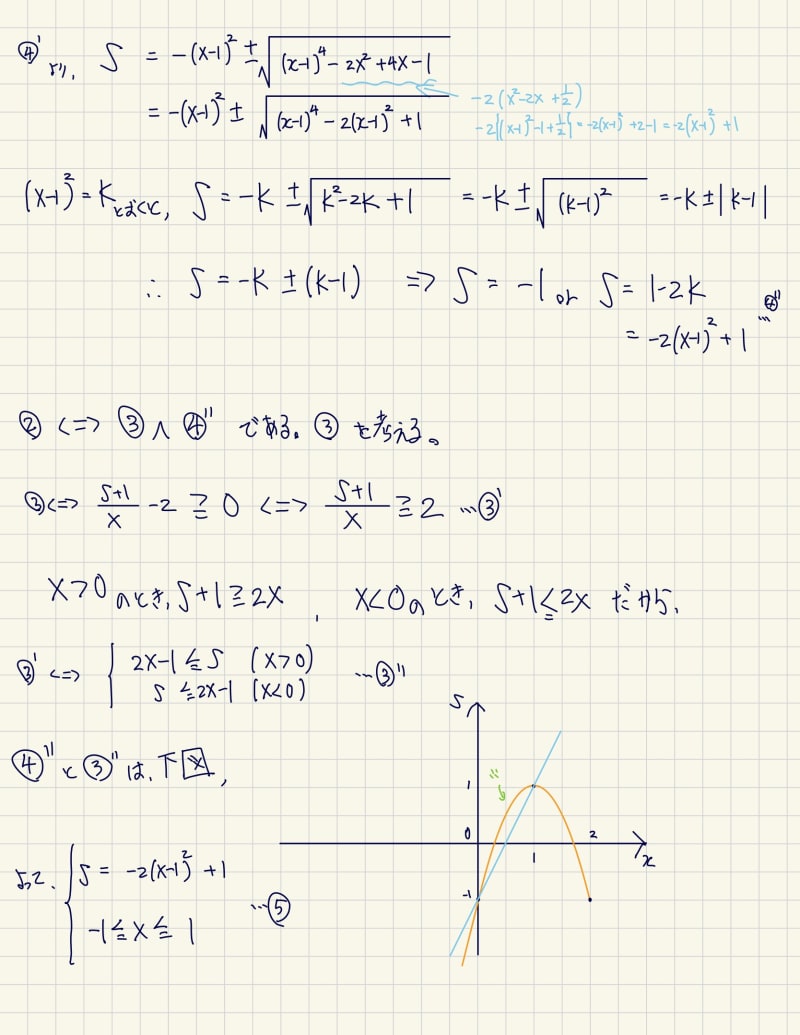
答えとしては、
(だだし)
になりました。
この問題は幾何で解くのが無難でしょう。三角形の内心を求めるということが1番の理由です。また、とが固定であること、動く点も半径の円周上の点であることから、三角形の2辺の長さとが常にであるということも解きやすくなる設定です。
1番楽に解けるのは、内心の位置ベクトルを使うやり方でしょうか。私は1番最初にこの解法が思い浮かびました。
いずれにせよ、数学の問題を解くにはいろいろなアプローチがあります。どうせなら楽に解ける方法を選べるように、解法・考え方を復習してみましょう。
暑さに負けず頑張ろう!応援してます!
回答ありがとうございます。
わたし、全くの末期ですね、、、、、、、、、、。
ちなみに何ですけど、このyってxを0から1で積分できますか?(高校生が)
この関数は模範解答の関数と一致していました。





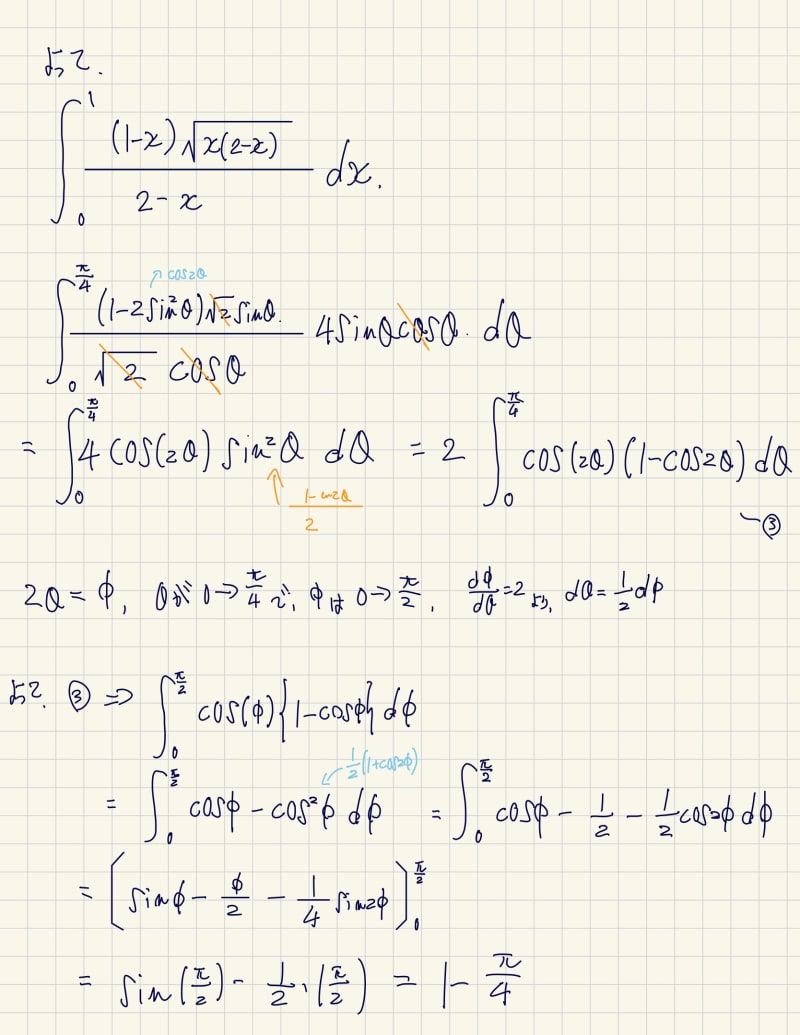

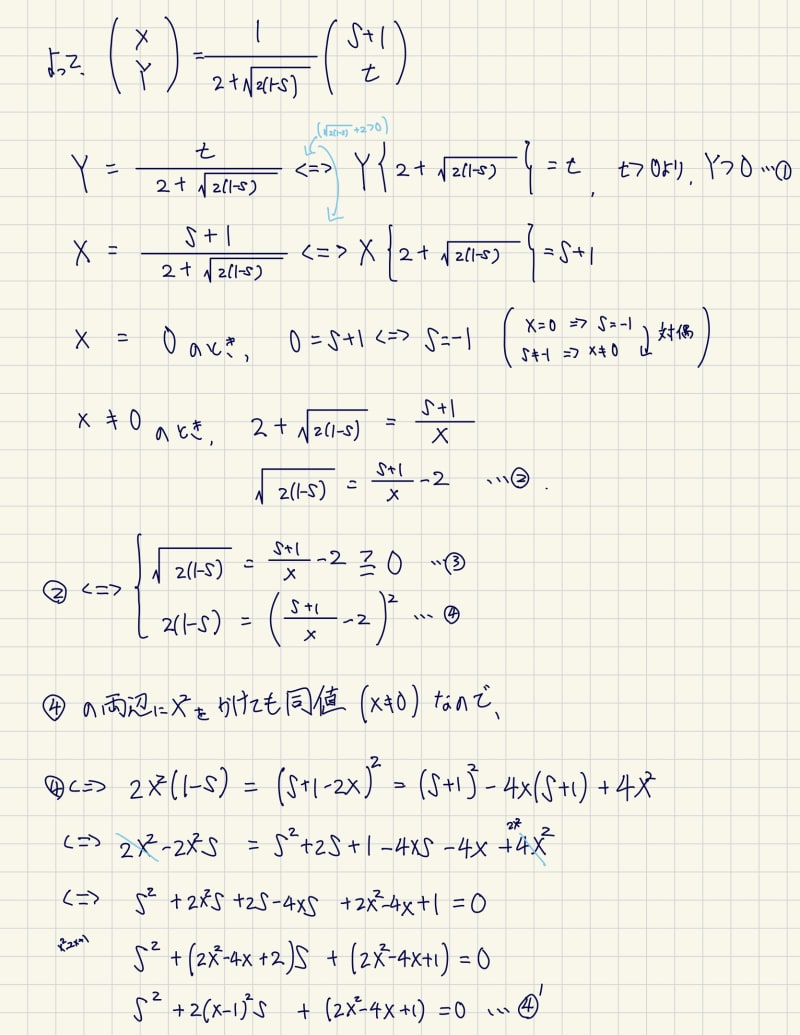







質問者からのお礼コメント
こまかなところまでありがとうございます。あのような強引(?)な積分ができることを知れて良かったです。内心の位置ベクトルの解き方も証明含めできるようにしておきます。また機会があればお願いします🤲